りんご さんの書込 (2007/01/27(Sat) 11:48)

【遮蔽電場の電荷分布をどう考えれば良いでしょうか】ーーー大学1年生に自然な説明ができる為にーーー

□ 発端 □

本来のスレッドは；

・電荷密度を積分する場合 けんさん（大学1年） 2007/01/18(Thu) 16:59 No.13775

です．これにつけて質問しようとしたのですが，手違えで，新規スレッドになってしまいました．でも，今回の質問は，けんさんのオリジナル質問を逸脱し始めているのと，スレッドが長くなり始めている事で，閲覧に支障をだしかねないとおもい，別スレッドとする事にしました．

□ 経緯 □

この問題を，MXKさんは，No.13895で，デルタ関数，階段関数を用い，数式ソフトによる処理で間違いの無い解説をお書きになりました．この少し前での No.13880での論議はとても参考になりました．

他方，私は，難しい論議も大切ですが，問題となっている原点から半径rの中にある電荷が具体的にどんなものかを知りたくて， No.13882で求めました．

その後，No.13902とNo.13903で，この電荷分布を遮蔽電場による電荷，Q_shield(r)と名付け，「No.13880の論議：電束密度の中心近傍の振る舞いから点電荷を推定する方法を静電ポテンシャルに適応」して原点近傍にある電荷量q_originを推定し，全体の電荷分布 Q_total(r) を求める事ができました．

この式は，MXKさんのだされている No.13895 と r_origin の内側を除いて一致します．一方はデルタ関数を仮定され，一方はある広がりを仮定しているだけの差です．

従って，一応の問題に答える事が出来て，目出度し愛でたしになった訳です．

□ 疑問点 □

ところが，今朝起きたときに，では No.13903の Q_shield(r)に出てくる点電荷とおもわれる定数項はどうして出てくるのか？？？？と思いました．

私は，学生の頃の不勉強の為に，湯川型ポテンシャルの勉強をした事がございませんし，電磁気の問題としても解いたのも今回が初めてであり，問題にある物理的背景もまるで存じません．

この問題の背景を含めて，ご解説をお願いできたらとおもいます．なお，デルタ関数のような近代的ツールは使わないで戴ければ幸いでございます．

りんご さんのレス (2007/01/28(Sun) 17:41)

自己コメントです．

湯川型ポテンシャルでウィキペディアを拝見すると；

• http://ja.wikipedia.org/wiki/%E6%B9%AF%E5%B7%9D%E3%83%9D%E3%83%86%E3%83%B3%E3%82%B7%E3%83%A3%E3%83%AB

・素粒子物理学での湯川ポテンシャル ・物性物理学での湯川ポテンシャル

とが在るようですね．私は，前者しか思い浮かべられなかったので，一年生の電磁気での課題とするにはやや理解できにくいと思いました．

でも物性物理や「溶液論でのデバイ-ヒュッケルのポテンシャル」のようにある荷電体があって，周りの物体による遮蔽を考えるというのならば，1年生の問題になり得ると思うようになりました．

せいぜいナブラやラプラシアンの極座標表示が問題でしょうが，球対称の公式をテンポラリに与えればすむ事ですね．

＝＝＝＝

電磁気学を初めて勉強されている皆さんに：

原点に置かれた電荷の解析で「デルタ関数が使えないと計算ができないとか，デルタ関数が使えないと，微分がら出来ないとか」と言った極論があるようですが，十分に咀嚼する事をお勧めします．

私も，学生の頃に，デカルト座標表示のデルタ関数を使った参考書で勉強しましたが；

（１）デルタ関数が無くても解析は出来ます．

（２）逆に，原点近傍のイメージが欲しいときには，デルタ関数をやめて，有限体積に分布した有限電荷濃度の分布を考えるようにしました．そうすれば，地球の中心で重力場が発散しないと同じ事で，有限で自然なイメージできるからです．

（３）勿論，多くの場合では，デルタ関数を使って，コンパクトで見通しの良い形で解析します，今でも．

やはり，大学1年生の頃には，あまり抽象的な計算に凝るよりも，通常の力学・電磁気の枠のなかで，物理的な洞察力と数学的記述との関連性を確実に感じ取っていただきたいと思います．

他方，上級の電磁気では，ガラッと視点を変えて，モダンなヴェクタ・テンサ解析や微分形式を駆使したマクスウェル方程式の世界に挑戦して戴きたいとおもいます．

その上で，電磁気と流体力学のような古典的な場をも統合的に扱えるような体系が出来ると良いですね．皆さんの中から，そんな分野の研究者が生まれると嬉しいですね．

MXK さんのレス (2007/01/28(Sun) 23:13)

出発点となる原理や方程式の数を少なくしたいと思うタイプの人には， あれやこれやの制約条件や適用限界を示すと嫌になるということもあります． ポアソンの式からクーロンポテンシャルが解析的に出ることぐらいは，一年では無理でも， グリーン関数などを学ぶ際などに調べておくとよいと思います．方程式に関する信頼も増しますし， 物理的な理解もより深まると思います．

今回の問題も逆方向にすれば 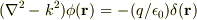を解くということなので，そのヒントにもなりますね．

りんご さんのレス (2007/01/29(Mon) 00:09)

>出発点となる原理や方程式の数を少なくしたいと思うタイプの人には， >あれやこれやの制約条件や適用限界を示すと嫌になるということもあります．

これは，少なくとも初学者さんの問題意識というか，方法論ではないと思います．おそらくMXKさんが，少なくとも場の理論ないしはその周辺を専門的に研究されている為に，我々，素人の思考形態との乖離が激しいのだと考えています．

もしも，仮に初学者でありながら，そのように発想するなら，その方の数学ないし物理数学の才は特殊なので英才教育を施すべきでしょう．MXKさんの周辺にはそのような学生さんが多いので，世の大半の学生さんもそうだと誤解されているように推察いたします．

逆に，『専門的に電磁気を扱われている研究者が，最小の方程式のセットにするために２種類のポテンシャルをベースに用いて，微分表現も従来法を用いないし，工夫したデルタ関数を用いて，見通しよく計算を進める』のに異論を挟むものではありません．しかし，この立場での論議する時には，「TPO」を配慮する事が重要と愚考致します．

>ポアソンの式からクーロンポテンシャルが解析的に出ることぐらいは，一年では無理でも，

ポテンシャル論を始める冒頭で，ラプラスの式を満たす解析解は「とても貴重で，1/rがそれなんだ」と教えるべきでしょう．で，簡易的にはデルタ関数で表現するが，色々な表現法もあるから，状況に合わせて考えやすい表式を行き来できるように教える必要がありますね．

私は，初学者のときには，物理数学で特殊関数を勉強すれば「ラプラスの式を満たす色々な解析解が出てくる」と思いわくわくしていて，がっかりしたものです．

>グリーン関数などを学ぶ際などに調べておくとよいと思います．方程式に関する信頼も増しますし，物理的な理解もより深まると思います．

最近の１年生は，物理数学でグリーン関数を学ぶのでしょうか？確かに，高校・大学・大学院の教育体系を大幅に革新する必要は感じます．しかし，現状では本当にグリーン関数を1年生が深く理解できるとは思いにくいですが．

推定では，MXKさんの主張される電磁気学は，学部3,4年生か，院・前期のテーマなような気がします．他方，この掲示板での質問は，高校生から大学生が主であると感じています．従って，回答側も，理論的な厳密さとか，エレガントな解法に力点を置かれるのは間違っているかと存じます．

最近，強く感じるのは，最先端のテーマの教科書を書くのは，最先端の研究者でしか無いでしょうが，学部生の教科書は，私のように「落ちこぼれ」が書いた方が，学生さんに理解しやすいのではと思うようになりました．天才・長島選手と天才・王監督との関係に似ているかも知れません．

今回の湯川ポテンシャルの論議で，拝見した「クーロンポテンシャルの粗視化」というタグで調べているうちに，流体力学の場を電磁気学的に勉強しようと購入していた「SGCライブラリ39マクスウェル方程式電磁気のよりよい理解のために」，北野正雄・著に論議されているのを知りました．

この雑誌（数理科学の臨時別冊：SGCライブラリ39）は，色々な意味で，現行の標準的な教科書の域をを踏み出しているものの，初学者・中級者には消化しにくい，いわゆる専門家しか判らない状態だと思いました．

＃しかしながら，この本は故・今井先生の「電磁気学を考える」に対する回答の一つとも思える．素人なりに強く評価したい． ＃このような著作が工学部の研究者から出されるという京都大学の懐の深さに今更ながら敬意を評します．

＃この記事をご覧になっている学生さんがいらっしゃいましたら，この雑誌をご覧になると，衝撃を受けると思います．ただし，第1〜3章は面白いものの荒削りすぎて混乱する事は必至でしょう．

逆に，このようなアプローチを噛み砕いて説明出来れば，我々素人にも，電磁気学や流体力学をモダンで使いやすく，しかも物理的イメージを豊富にして理解できるヒントが多数かいてあるように思えます．

しかし，現実問題として，過渡的にも教育方法を初学者むけに暫定改訂する必要もあろうかと感じます．

いずれにしろ，私自身は，アドバンスな解説を戴ければ，興味深く拝見したいとおもいますが，それなりに用語とか数学的手法に付いては，吟味いただきたいと思います．たとえば， ・粗視化 ・グリーン関数 ・束管 などの用語は，式や図をいれて解説されないのなら持ち出すべきではないと思います．

逆に，大学等で教育に携われているのならば，研究室のウェブ・サイトなどでの解説資料を利用して解説いただければ，とても素晴らしいと愚考いたします．

最後に，もう一度お願いしたいのは，この掲示板を見に来る平均的な読者や，私のような素人解説者には，使い勝手がそこそこの道具を，直感的に使い切る事が大切です．中途半端に先進的な道具の一部を持つと，怪我をしやすくなることをご理解いただければ幸いです．

MXK さんのレス (2007/01/29(Mon) 13:56)

>>ポアソンの式からクーロンポテンシャルが解析的に出ることぐらいは，一年では無理でも， >>グリーン関数などを学ぶ際などに調べておくとよいと思います．方程式に関する信頼も増しますし，物理的な理解もより深まると思います． >最近の１年生は，物理数学でグリーン関数を学ぶのでしょうか？確かに，高校・大学・大学院の教育体系を大幅に革新する必要は感じます．しかし，現状では本当にグリーン関数を1年生が深く理解できるとは思いにくいですが．

正確に読んでいただきたいと思います．「グリーン関数を学ぶ際」が１年であるとはいっていないつもりです．電磁気は電磁気学の授業だけで学ぶものではなく，数学の応用問題としても登場しますので，そういう場面を念頭においています．

りんご さんのレス (2007/01/29(Mon) 14:25)

>正確に読んでいただきたいと思います．「グリーン関数を学ぶ際」が１年であるとはいっていないつもりです．電磁気は電磁気学の授業だけで学ぶものではなく，数学の応用問題としても登場しますので，そういう場面を念頭においています．

う〜む．やはり，先にお書きになった， >出発点となる原理や方程式の数を少なくしたいと思うタイプの人には， >あれやこれやの制約条件や適用限界を示すと嫌になるということもあります． >ポアソンの式からクーロンポテンシャルが解析的に出ることぐらいは，一年では無理でも， >グリーン関数などを学ぶ際などに調べておくとよいと思います．方程式に関する信頼も増しますし，物理的な理解もより深まると思います．

この文脈のなかから，電磁気以外の物理数学を思い浮かべる事は，素人には不可能です．やはり，大変失礼言い方ですが，一般人の思考形態をもうすこし勉強なさらないと，善意で指導されているお積もりでも，誤解されるようにも思います．

ただ，私自身は，国語力も低く，数学的能力が低く，細かなところのニュアンスを理解できませんし，自分の感触が絶対とも思えません．

しかし，突然に，文脈と関係の薄い積分方程式がでてくるような解説を私だったらしません．基本は，いま課題として取り上げた点を，どのような観点から眺め，どのようにして理解して行くかが問題でしょう．いわば，本道を外れた枝葉について細かな論議をされるのは，たとえ相手が素人と言えど，フェアな論議にはならないと思います．

ここは物理の課題を論議する掲示板です．たとえ，論者が中学生であろうと，私のような老人であろうと，大学の研究者であろうと，論議する上では対等の立場であることを踏まえて戴きたいと愚考します．

なお，本スレッドの先頭に「ーーー大学1年生に自然な説明ができる為にーーー」という副題をつけています．この点を正確に読んでいただきたいと思います．

MXK さんのレス (2007/01/29(Mon) 20:21)

りんごさん，

物理的でない議論をこれ以上展開するつもりはありませんが， 今回の問題については，初学者向け(大学1年レベル)での考え方はすでに 提示されていると理解しています．スレッドの終了も宣言されています． その後の議論は，余談として，原点の点電荷をスッキリとらえたいという視点から，進んで いるので，一年生向きでない方法や用語が出てきても仕方がないと思います． 一旦，本質が捉えられたら，それを噛み砕いて説明することも可能かもしれません．

りんご さんのレス (2007/01/29(Mon) 22:00)

MXKさん，

>物理的でない議論をこれ以上展開するつもりはありませんが，

素人論議に巻き込んでご免なさい．

しかし，なにが何でも高等数学を使わないと物理的な考察ができないというのは，物理屋のコモンセンスを逸脱しているようにも感じます．きっと私が間違っているか，MXKさんが数学系の方かなとも推測しています．

>今回の問題については，初学者向け(大学1年レベル)での考え方はすでに提示されていると理解しています．

私としては，まだ論議が不十分と考えたからこそ，このスレッドを立ち上げました．今すぐに調べられませんが，物性ないし電解質の論議で，遮蔽型ポテンシャルがどのように展開されているか勉強して，判ったらこのスレッドに書き込むつもりです．

>スレッドの終了も宣言されています．

どこにそのような事が書かれているのでしょうか？私は見ていません．

＃念の為に確認しましたが，ご本人の終了宣言は出ていないようです．

>その後の議論は，余談として，原点の点電荷をスッキリとらえたいという視点から，進んでいるので，一年生向きでない方法や用語が出てきても仕方がないと思います．

ここが見解の相違だろうと思います．それならそれで，宣言してから論議されるべきでしたね．それこそ，スレッドを良く観察ください：「正確に読んでいただきたいと思います．」です．

お二人の論議を拝見していて，ご専門は数学ないしは物理数学で，日頃，理論的な研究に没頭されているのでは無いかと想像するにいたりました．泥臭い物理の落ちこぼれとは，論議が噛み合ないのはしかたがないように拝察されます．

>一旦，本質が捉えられたら，それを噛み砕いて説明することも可能かもしれません．

これについては，依存ございません．その節には，是非ともご自分のサイトに発表される事を期待いたします．

以上，論議上の良い経験を得る事ができました．有り難うございました．