分岐する管内の流れ
分岐する管内の流れ
まさ さんの書込 (2007/01/20(Sat) 04:26)
初めてお世話になります.
流体力学の問題で躓いております. 以下のような問題です. 図のような(リンク先にて画像掲示板をお借りしております.見づらい図で申し訳ありません)T字型の分岐管路がある.
管摩擦係数を  (一定),流体の密度を
(一定),流体の密度を  (一定),圧力を上流側,下流側でそれぞれ
(一定),圧力を上流側,下流側でそれぞれ 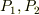 ,管の直径を
,管の直径を  ,
, 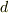 とし,分岐による損失はないものとする.
とし,分岐による損失はないものとする.
この時の流量 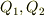 を求めなさい.
私はこの問題は分岐管出口での流速を求めれば流量が分かるだろうと思い,連続の式,損失ヘッド,ベルヌーイの式を習っていましたので,それらを適用すればいいだろうと思い,入り口での流速を
を求めなさい.
私はこの問題は分岐管出口での流速を求めれば流量が分かるだろうと思い,連続の式,損失ヘッド,ベルヌーイの式を習っていましたので,それらを適用すればいいだろうと思い,入り口での流速を 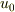 ,上側の出口での流速を
,上側の出口での流速を 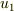 ,もう一方での出口での流速を
,もう一方での出口での流速を 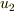 とおいて,連続の式から,
とおいて,連続の式から,
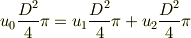
ベルヌーイの式から,
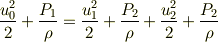
圧力損失から,
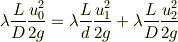
とし,流速を求めた結果,
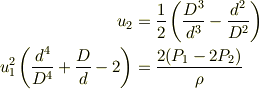
と言う関係まで導き一応目的と言えるものまでは導けました.
しかし解の形がやけに煩雑であり,解に自信が持てず困っております. 最初の3式の立式の時点で間違っていそうな気がしますが,ここから先に進みません.
どのように解いていけばいいのか方針等ご助力いただきたいです.宜しくお願いいたします.
Re: 分岐する管内の流れ
zoro さんのレス (2007/01/20(Sat) 14:26)
始めまして.
私も流体力学を知りたいのですが,まだ運動方程式の中途にいます.そこで,回答は出来ませんが,一般的な逆質問があります.
(1) 初めの流れu0が二つの流れu1,u2に分かれた訳ですから, このu1,u2の解は,対称的になると思いますが,如何でしょうか?
- P0が解の中に出てこないのが,奇異に感じますが?
一つの手として,u1,u2の流れの径をD1,D2見たいに書き換えて,方程式を対称的にすると,面倒かもしれませんが,計算ミスが少なくなるかもしれませんね.
Re: 分岐する管内の流れ
まさ さんのレス (2007/01/20(Sat) 14:31)
zoro様返答感謝いたします.
>このu1,u2の解は,対称的になると思いますが,如何でしょうか? 確かにそのような感じはします.
>(2) P0が解の中に出てこないのが,奇異に感じますが?
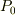 というものは大気圧でしょうか?
私は圧力に関しては
というものは大気圧でしょうか?
私は圧力に関しては 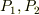 以外の者は出ようがないと思います.
以外の者は出ようがないと思います.
Re: 分岐する管内の流れ
zoro さんのレス (2007/01/20(Sat) 18:30)
>私は圧力に関してはP_1,P_2以外の者は出ようがないと思います.
これは遡って >ベルヌーイの式 の左辺で,P1と置かれているのに起因しませんか?
私はこの式は,外力が保存力の場合にスカラー部の保存法則(エネルギーの保存と呼でいいのかも)から出てくると思います.ですから,左辺は上流部の点0での速さu0,圧力P0であって,他の場所の値を気楽に書けないと思います.同様の論議をすると下流の点1,点2に付いても同様では無いでしょうか?
勿論,他の法則による別の式が存在するなら別だと思います.
追伸 P0=P1らしいことに気が付きました.ということなら,計算上は

と置いておいて,最後に 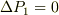 とでもすれば,計算は面倒でも,数式の意味は判り易くなると思います.
とでもすれば,計算は面倒でも,数式の意味は判り易くなると思います.
式の物理的な意味合いから論議できずに,御免なさい.
Re: 分岐する管内の流れ
まさ さんのレス (2007/01/20(Sat) 22:11)
返信有り難うございます.
流体もしくは水力学でエネルギー保存の式としてベルヌーイの式を習いましたが,
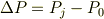
とする意味がやはりよく分かりません. 申し訳ありません.
おそらく,求めるべき変数は速度の3つなので何かしらの3式を立てるのだとは思います.
Re: 分岐する管内の流れ
nibbana さんのレス (2007/01/22(Mon) 11:54)
はじめまして. 理学系出身なので水力学は良くわからないのですが,ちょこっと本を見てみました.
3つの式について, 第一式: 管の直径がすべてDなのは書き込む際のタイプミスでしょうか?
第二式: ベルヌーイの定理の式は,流線に沿って考えるのだから, 出口が2つあることに対応して,2本必要ではないでしょうか. (出口が2つあるからといって,一本の流線が二股に分れるわけではないから)
第三式: 損失ヘッド(エネルギーの損失)というのはベルヌーイの定理の式に 含めるもの. まささんの式は,損失ヘッドに関する保存則とでも言うような形に なっていますが,そのような関係は成り立たないように思います.違うでしょうか?
Re: 分岐する管内の流れ
まさ さんのレス (2007/01/23(Tue) 21:20)
nibbana様返信有り難うございました.
結論から言うとnibbana様の仰るとおりでした.
3つの式について 第一式は私のタイプミスでした. ベルヌイの式を改めてたてなおし
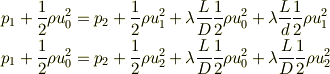
としました.
Re: 分岐する管内の流れ
nibbana さんのレス (2007/01/24(Wed) 02:45)
私の意図した式もその通りです.
なおこの種の計算では,L/D および L/d が十分大きく,
そのため摩擦損失の項が大きいことから速度ヘッドを無視するようです(本日気がついた次第,申しわけありません).
まささんの式の 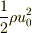 などです.
などです.
そうするとベルヌーイの式は,圧力の項をすべて左辺にまとめて,
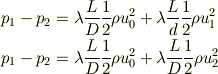
の形になります.
Re: 分岐する管内の流れ
まさ さんのレス (2007/01/29(Mon) 17:15)
nibbana様有り難うございました.
ついでと行っては失礼なのですが,もう一も分からない問題があります. 回流路の流れなのですが,
図に示すように途中に自由表面を持つ十分大きなタンクを取り付ける.内径d,全長Lのこの回流路を流量Qで回流させるために取り付けるポンプのヘッドを表せ.と言う問題です.
管摩擦係数  のみ考えよ.
と言う問題なのですが,これはタンクがなければ
のみ考えよ.
と言う問題なのですが,これはタンクがなければ
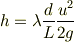
を流量であらわせばよいと思うのですが, この場合などはC-D,D-A,A-Bに分けて考えればよろしいのでしょうか. その場合などはポンプに流入する流量と流出する流量,ポンプの高さを一定の|2510c39011c5be704182423e3a695e91|などとおいて解けばよいのでしょうか.
お力添えの程宜しくお願いいたします.
Re: 分岐する管内の流れ
まさ さんのレス (2007/01/30(Tue) 00:48)
もう少し考えてみたのですが,私はこの場合は,タンクの出口と入り口の位置の差がない限りは(諸損失を考慮しなければ)ヘッドはタンクのない場合と変わらないと思うのですが,何故そうなるかが確認がとれません.
Re: 分岐する管内の流れ
nibbana さんのレス (2007/01/31(Wed) 01:49)
あまり管路の話を私にふられても困ってしまいますが--良く知ってるわけではないので.
この問題で途中に水槽があることの意味は恐らく, "水槽で水流は,大気圧という固定した圧力にさらされる" ことでしょう.また,管内の圧力が極端に大きくなったり 小さくなったりするのを防ぐのかもしれません.
水槽から出発して,グルっと管路を一周してもどってきたとき, 最初と最後で圧力が同一で,そのため全問と違って,圧力差で水流を保つことは できません.だから,ポンプによるエネルギー供給とエネルギー損失がつりあう, として計算するのでしょう.
--あくまでいいかげんな予想です. あしからず.
Re: 分岐する管内の流れ
まさ さんのレス (2007/02/01(Thu) 02:23)
nibbanaさん,不得手な分野にもかかわらず返答有り難うございます.
タンクはサージタンクのようなものであるので,圧力差ではなくnibbanaさんの仰るとおりエネルギー供給,損失から考えれば,やはり(揚程としては)タンクのない場合の揚程と同じではないか,と思いました. (十分に大きなタンクであるので管路の位置が変わらなければヘッドに変わりはないと考えました.)
私もちょっといい加減すぎるかもしれません. 勉強不足を痛感しました.