カリプソ さんの書込 (2007/01/20(Sat) 01:56)

物理で液体窒素を用いた実験をしたのですが，疑問が生じたので質問させてください． 普通に膨らませた風船とHeの入った風船の表面を液体窒素の液面に軽く接触させて冷却し，その様子を観察しました．結果は普通に膨らませた風船の方がぺちゃんこになったのですが，これは窒素や酸素は液化するがヘリウムは気体として存在するからという解釈でよろしいですか？

それと，（こちらの方がメインの質問です）ヘリウムの方が速くしぼみ，また取り出すとヘリウムの方が速くもとに戻ったのですが，その要因はなんなのでしょうか．熱膨張率が関係しているのでしょうか．

zoro さんのレス (2007/01/20(Sat) 02:22)

Heの音速は，空気とかなり違いませんでしたか？

カリプソ さんのレス (2007/01/20(Sat) 02:44)

＞Heの音速は，空気とかなり違いませんでしたか？ Heの音速とは何ですか？

toorisugari no Hiro さんのレス (2007/01/20(Sat) 04:13)

熱伝導率の違いはどうでしょうかね．

yama さんのレス (2007/01/20(Sat) 09:11)

前半はそれでいいと思います．

後半ですが，液化するときには凝縮熱を放出するのに時間を要するのでしぼむのが遅くなり，気化するときは気化熱を吸収するのに時間を要するので膨らむのが遅くなるのだと思います． また，ヘリウムは単原子分子気体であり，２原子分子気体の酸素や窒素より比熱が小さいために温度変化が速いというのも一因でしょう． 熱伝導率も大きく関係すると思いますが，熱膨張率については差は少ないのであまり関係ないでしょう．

カリプソ さんのレス (2007/01/22(Mon) 00:42)

いつもお世話になっています． 熱伝導率をウィキペディアで調べてみたところ，窒素，酸素，ヘリウムそれぞれ，0.02598W/mK, 0.02674W/mK，0.152W/mK となっており，大分差があることがわかりました． ありがとうございました．

toorisugari no Hiro さんのレス (2007/01/22(Mon) 20:01)

> 気化するときは気化熱を吸収するのに時間を要するので膨らむのが遅くなるのだと思います

そうですよね．でも気化熱だけだと時間の次元が出てこないので，気化熱と熱伝導率（と必要なら比熱，密度等）からmol/sのような量が出せると良いのですけど．．． 私にはわかりませんでした．

yama さんのレス (2007/01/22(Mon) 23:06)

その通りだと思います．熱を吸収するのに要する時間は熱伝導率に関係するでしょうね． しかし，気体の部分と液体の部分があって，風船の周囲には空気があるので，これらすべての熱伝導率が関係すると思います． しかも，気体や液体では対流による熱輸送もあるので，簡単な計算では求められないように思います．

zoro さんのレス (2007/01/23(Tue) 01:18)

以前書き込みをした後に，フォローを書いたのですが入力エラーになったまま忘れていました．

私は，オーダ・エスティメーションのやり方を書いてみます．概算をしたいときに有効かも知れません．

＝＝＝＝

>Heの音速とは何ですか？

一般に，気体分子運動のイメージから考えると，熱伝導とか濃度拡散は運搬する対象が「運動エネルギ」や「気体濃度」と異なるものの，大雑把にいって分子運動の速度の自乗の平均値 によって運ばれると考えます．

他方，エネルギ等分配の法則から

従って，凡その当りをつける場合，速さの概算値，

この段階で，平均速度〜音速が概算できると思います(勿論きちっとした式はありますが)．すなわち，上記の式から，気体の温度と分子量への依存性は大雑把に判りますね．

次に液体窒素の沸点は約70°Kで，常温は300°Kで，温度差，?T≒200°Kと大きい事が特徴ですね．

ある単位体積あたりの物理量Wが体積Vの内部から,表面Sにむけて単位時間に流入する量Rは

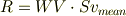
で与えられます．

そこで常温から風船を液体窒素に入れるときにはWとして分子数密度ρを取れば濃度の拡散速度がでると思います．簡単な気体の状態方程式,PV=nRTから；

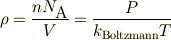
Wとして気体の内部エネルギに取れば，熱量の拡散速度がでると思います．その場合，分子の運動自由度fとすると

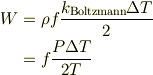
で概算できると思いますが，如何でしょう．ちなみにHeは単一原子気体なのでf=3,窒素や酸素は2原子分子ですから回転と振動の自由度がありf=5ぐらいで近似できるとおもいます．

緊急に概算したい時の便法ですが．