干渉や定常波におけるエネルギー

ｅKinetic さんの書込 (2007/01/19(Fri) 12:26)

ニュートンリングで，上から見たときに明環ならばその位置は下から見ると暗環になります．これをエネルギーの観点からみると，１００のエネルギーのうち反射が９５ならば，透過が５であるとして理解できます．

ヤングの干渉や回折格子の干渉で，強めあいや弱めあいにおけるエネルギーは，どのようになっているのでしょうか．弱めあっている部分から強めあっている方へエネルギーが回るのか（光子の数が少ないか多いかという観点からはこれが正解か），あるいは弱めあっている部分は，スクリーンにエネルギーが吸収されていると考えるのでしょうか．

定常波についても節や腹におけるエネルギーがどうなっているのかわかりません．節では定常波のエネルギーはおそらくゼロなのだと思いますが，互いに逆向きに進む２つの波のエネルギーが，節の部分でゼロになっても，その先に進んでいけるのかどうか，疑問になっています．またもし，節でゼロ，腹で最大なら，振動源が一定なエネルギーを送り出していても，定常波ではエネルギーが局在している（とびとびになっている）ことになりますが，それは特におかしいことではない（ありえる現象な）のでしょうか．

どうぞよろしくお願いいたします．

Re: 干渉や定常波におけるエネルギー

ｙama さんのレス (2007/01/19(Fri) 17:35)

後半の質問について書いておきます．電磁波の定常波の場合，電場波の節の位置と磁場波の節の位置は４分の１波長ずれています．そのため，電場の節の位置でも磁場は0ではないので，磁場のエネルギーがあることになります．そのエネルギー密度は時間的に変動しますが，ポインティングベクトルは0になるので，節を通過するエネルギーの流れはありません．

ばねを伝わる疎密波の場合と比較して考えると分かりやすいかもしれません．ばねの定常波では，節は動かないので，そこでの運動エネルギーは0です．しかしばねの疎密の変化があるので，時間的に変動する弾性エネルギーがあります．

Re: 干渉や定常波におけるエネルギー

yama さんのレス (2007/01/19(Fri) 23:15)

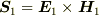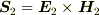前半についてですが，古典論の範囲で考えると，エネルギーの流れはポインティングベクトルで表すことができます．ポインティングベクトル $\bm{S}_1=\bm{E}_1\times\bm{H}_1$ と $\bm{S}_2=\bm{E}_2\times\bm{H}_2$ の２つの電磁波が重なったとき，合成波のポインティングベクトルは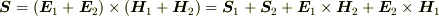， $\bm{S}=(\bm{E}_1+\bm{E}_2)\times(\bm{H}_1+\bm{H}_2)=\bm{S}_1+\bm{S}_2+\bm{E}_1\times\bm{H}_2+\bm{E}_2\times\bm{H}_1$ となります．つまり２つのポインティングベクトルを単純にベクトル加算したものにはなりません．このポインティングベクトルは時間的に変動しますが，平均的なエネルギーの流れとしては，波源から出たエネルギーが次第に特定の方向すなわち強め合う方向に集中していくものと思います．

量子論では，光子がエネルギーを運ぶわけですが，個々の光子の軌道というものは意味を持たないので，平均的なエネルギーの流れを考えれば，やはり古典論と同様の結果になると思います．

Re: 干渉や定常波におけるエネルギー

yama さんのレス (2007/01/19(Fri) 23:44)

>またもし，節でゼロ，腹で最大なら，振動源が一定なエネルギーを送り出していても，定常波ではエネルギーが局在している（とびとびになっている）ことになりますが，それは特におかしいことではない（ありえる現象な）のでしょうか．

おかしくはないと思います．たとえば，波源から壁に向かって進む波と，壁からの反射波が重なって，波源と壁の間に定常波ができている場合について考えてみましょう．このとき，波源から壁に向かうエネルギーの流れと，壁から波源に向かう（反射波の）エネルギーの流れが考えられますが，同じ大きさで逆向きなので，波源と壁の間の正味のエネルギーの流れは0です．また，反射波のエネルギーの流れとしては，波源から壁と反対向きに進むものもあります．結局，正味のエネルギーの流れを考えると，波源から送り出されるエネルギーは，定常波の部分には供給されず，壁と反対の方向に向かうことになります．

Re: 干渉や定常波におけるエネルギー

eKinetic さんのレス (2007/01/20(Sat) 14:03)

丁寧な説明をいただきながら，お礼が遅れてすみません．

>平均的なエネルギーの流れとしては，波源から出たエネルギーが次第に特定の方向すなわち強め合う方向に集中していくニュートンリングの場合は，ガラスに入射してからの干渉だが，ヤングの場合は，スクリーンに到達するまでが干渉の過程であって，到達したときにはすでにエネルギーの強弱ができている−ということで納得できました．

>電磁波の定常波の場合，電場波の節の位置と磁場波の節の位置は４分の１波長ずれています． >ポインティングベクトルは0になるので，節を通過するエネルギーの流れはありません．ポインティングベクトルが0になるのは，電場波の節と磁場波の節のどちらにおいても0，つまり１波長につき４ヶ所ある，ということでよいでしょうか．疎密波との比較はたいへんわかりやすかったです．ですが，節を通過するエネルギーの流れがないのなら，節と節の間の腹にはどのようにエネルギーが伝わっていくのか，疑問が残ったままでいます．波源が振動をやめれば，明らかに定常波がなくなるわけですから，節と節の間にも，節を通してエネルギーが伝わっていくようにみえます．弦の定常波やばねを伝わる疎密波の定常波において，動かないとされる節でも，節の部分の媒質の内部構造が（分子レベルで）動いてエネルギーを伝えていくのではないか，と私は考えていました．

No.13797については，納得できました．

yamaさん，ありがとうございました．

Re: 干渉や定常波におけるエネルギー

クロメルさんのレス (2007/01/20(Sat) 17:35)

ちょうどそのことに関する本（ディラックの"The Principles of QuantumMechanics"）を読んでいたので質問の前半に答えることができそうです．ヤングの干渉実験でエネルギーを考えるには，量子力学的な考え方をしなくてはなりません．二つの光子が干渉を起こし消えたり倍増したりするのではなく，光子は自分自身と干渉するそうです．つまり，光子は部分的に右のスリットを通り，部分的に左のスリットを通るということです．そうすることで，二つの波動関数（存在確率の波）が干渉を起こし，スクリーン上に濃淡をつくるというのです．波動関数の節の部分では，存在確率がゼロなので電子がぶつかることはありません．他の光子とは干渉せず，自分自身と干渉するんです．こうしてひとつの光子はスクリーン上にひとつの衝突を起こすのでエネルギーは保存されるそうです．波動関数同士が干渉を起こすなんて不思議な話ですよね．

Re: 干渉や定常波におけるエネルギー

yama さんのレス (2007/01/20(Sat) 18:42)

>ポインティングベクトルが0になるのは，電場波の節と磁場波の節のどちらにおいても0，つまり１波長につき４ヶ所ある，ということでよいでしょうか．

よいと思います．

>波源が振動をやめれば，明らかに定常波がなくなるわけですから，節と節の間にも，節を通してエネルギーが伝わっていくようにみえます．

必ずしもそうではありません．確かに No.13797 の例では，波源が振動をやめれば，波は壁と反対側に進んでいってしまって定常波がなくなりますが，波が外に出られないようにすれば定常波が存続します．たとえば，両端を固定した弦を適当に弾くと，固定端を節とする定常波ができ，弾いたあともしばらくは定常波が存続します．もちろん周囲の空気の振動（音）としてエネルギーが失われるので，振動はだんだん減衰していきますが，もしエネルギーが失われなければ，定常波はいつまでも存続するでしょう．この場合何かの波源からエネルギーが供給されているわけではありません．また，節を通過するエネルギーもありません．節を通じてエネルギーが供給されることによって振動が続くのではなく，エネルギーの出入りがないため，節と節の間のエネルギーが一定に保たれて振動が続くわけです．この場合の定常波を互いに逆向きに進む進行波の重ね合わせと見なせば，進行波が弦の両端で反射するので，外部に出ることなく閉じこめられていると考えることもできます．

なお，ヤングの実験を光の粒子性と両立させて説明するには量子論が必要ですが，粒子性を無視すれば古典論でも説明できます．

Re: 干渉や定常波におけるエネルギー

eKinetic さんのレス (2007/01/21(Sun) 14:56)

クロメルさん： >二つの波動関数（存在確率の波）が干渉を起こし，スクリーン上に濃淡をつくる... >波動関数同士が干渉を起こすなんて不思議な話ですよね．

古典論では，一方のスリットからの波（おそらく電場の振動）を 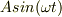$Asin(\omega t)$ ，他方からの波を 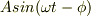$Asin(\omega t-\phi )$ として和を求め，結果の振幅を２乗して，光の明るさの強度分布を計算します．これが量子論の波動関数同士の干渉に対応するのかな，と推測しましたが，たぶん間違っているのでしょうね．

勉強しなければならない課題が多すぎて，このあと量子論までたどり着けるのかどうか... クロメルさん，ありがとうございました．

yamaさん：何度もすみません． >節を通じてエネルギーが供給されることによって振動が続くのではなく，エネルギーの出入りがないため，節と節の間のエネルギーが一定に保たれて振動が続くわけです．

エネルギーが失われない場合のこの部分の説明については，すごく納得できました．しかし，現実には減衰します．それを波源が，節の外からエネルギーを与え続ける事によって，定常波を継続させているような気がするのです．

私の定常波に対する基本的なイメージは，

http://www2.biglobe.ne.jp/~norimari/science/JavaEd/wave4.html

の Show Compon. にチェックを入れた状態です．

節が節であるためには，左右から波が次々とくる必要があり，そのことは，節を通してエネルギーが流入していることになるのではないかと思えるのです．

Re: 干渉や定常波におけるエネルギー

yama さんのレス (2007/01/21(Sun) 20:48)

>しかし，現実には減衰します．それを波源が，節の外からエネルギーを与え続ける事によって，定常波を継続させているような気がするのです．

確かに現実には何らかのエネルギーの散逸があるので振動は減衰します．その意味では，エネルギーを供給し続けないと振動がいつまでも持続することはありません．たとえば弦の一端に音叉をとりつけて音叉を電磁力で強制振動させれば，弦の定常波が持続するように見えます．しかし，この場合は定常波のように見えても真の定常波ではなく，節のように見える部分もわずかに振動します．従ってその部分をエネルギーが通過することができます．真の定常波では，節の部分は全く振動しないのでエネルギーは通過できません．

>節が節であるためには，左右から波が次々とくる必要があり，そのことは，節を通してエネルギーが流入していることになるのではないかと思えるのです．

両端を固定した弦の場合は，両端で反射した波が左右から次々ときて重なって定常波ができます．もちろん現実には両端での反射率は100％ではないし，それ以外のエネルギーの散逸もあるので，振動は減衰します．しかし，理想化した状態として，両端での反射率が100％で，それ以外のエネルギーの散逸もなければ，定常波はいつまでも存続します．この場合，外部からのエネルギーの流入はありません．定常波を互いに逆向きに進む波の重ね合わせと考えれば，互いに逆向きに同量のエネルギーが節を通過すると考えることもできますが，それは全体としてはエネルギーの通過はないということです．