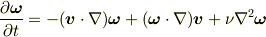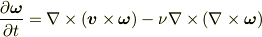粘性流体
粘性流体
テツ (大学3年) さんの書込 (2007/01/10(Wed) 21:45)
初めまして.大学で主に流体力学を勉強しているものです.
流体力学の質問です.
中心の周りをωで回転する円形の水の層で中心から流量Qの湧き出しがある場合の速度ベクトルvを求めるという問題です.
条件は流体は非圧縮粘性流体,円の外は吸い込み,深さは一様である,遠心力は考えなくてよいという条件です.
・ナヴィエ-ストークス方程式
・ 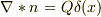 ・
・ 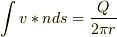
の三式を連立すればよいと思ったのですがうまく行かなくて困ってます. 何かうまい解き方などご教授下さい.よろしくお願いします.
Re: 粘性流体
りんご さんのレス (2007/01/10(Wed) 22:30)
初めまして.
流体力学はほとんど知らないのですが,
- どのような空間で論議するのでするのでしょうか.回転面だけの2次元空間とか,上下方向も考えて3次元なのか,はたまた2次元だが,同心円で考えて1次元だとか.
2)表式が通常の解析と違うようですが,普通に表せませんか?「*」は?
- 「n」は何ですか?
4)運動方程式も含めて,全ての式を書き下していただけませんか?
初めまして
テツ (大学3年) さんのレス (2007/01/11(Thu) 00:12)
りんごさん,わかりにくくてすみません.よく見るとめちゃくちゃでした.
深さは考えなくてよいということで,三次元ですが回転面(断面)での議論です.Z軸を回転軸として円柱座標で主に自分は計算しています.
|0f7f0c35b5d4f171f5f2f032b2f55d64|n|cbb184dd8e05c9709e5dcaedaa0495cf| は単位法線ベクトルです.
・  omega|0f186ed765be60fb0069d0a95a2fcadb|v|90c6eaa4f2e9bb42390227a72e94d263|omega|16d65940b8e8e5c2b4ebfc15df1e881b|omega|90c6eaa4f2e9bb42390227a72e94d263|v|b6e8bf55681898d5f35d43359647b486|omega|cbb184dd8e05c9709e5dcaedaa0495cf|
・ |b29cc13864fc6842044cd4ba4f45f26c|n|af580a61d6034f23eba4645f69964885|
・ |86e8ba480f59c01c43d143ec3c42092e|v|e6664c6afd575057a5746ab937318ee1|n|dffd42b6905df89a1d045026cb265f11|
omega|0f186ed765be60fb0069d0a95a2fcadb|v|90c6eaa4f2e9bb42390227a72e94d263|omega|16d65940b8e8e5c2b4ebfc15df1e881b|omega|90c6eaa4f2e9bb42390227a72e94d263|v|b6e8bf55681898d5f35d43359647b486|omega|cbb184dd8e05c9709e5dcaedaa0495cf|
・ |b29cc13864fc6842044cd4ba4f45f26c|n|af580a61d6034f23eba4645f69964885|
・ |86e8ba480f59c01c43d143ec3c42092e|v|e6664c6afd575057a5746ab937318ee1|n|dffd42b6905df89a1d045026cb265f11|
 は粘性率です.
は粘性率です.
Re: 初めまして
りんご さんのレス (2007/01/11(Thu) 01:33)
>深さは考えなくてよいということで,三次元ですが回転面(断面)での議論です.Z軸を回転軸として円柱座標で主に自分は計算しています.
という事は,Δz=1の単位厚さの液体を考えると思っても良く,また溶液と同期して回転する回転系でみても遠心力の項は無すると言う事ですね.
#自分のイメージでは,無限に長い直径がゼロの電流がつくる #磁場みたいに考えてみます.
円柱座標という事ですが,お使いの座標成分を明示していただけませんか.推定では, 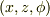 とか.
とか.
さて,第1式は,運動方程式(NS-Eq)の回転をとったものですか?従って,
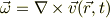
でしょうか?
次の式は速度場の発散が,その地点でのわき出しだけを表しているので;
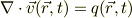
題意から,わき出し量は原点だけにあるので;
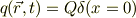
とすると,この場合の「単位法線ベクトル」は何を意味するのでしょうか?
さらに,第3式は,速度場の発散の積分形でしょうか?
まだ,さらに質問です.速度場や渦度を具体的に成分表示していただけますか?
質問ばかりで,ごめんなさい.なお,式をフォローするので一杯だったのですが,ひょっとして,時間に関して定常の解で良いのでしょうかね?
Re: 初めまして
テツ (大学3年) さんのレス (2007/01/11(Thu) 03:00)
ご質問,ありがとうございます.
時間に関して一定の時間まで(回転を始めて安定するまで?)の変化がわかるような式が導けたらベストなのですが,それをやるには少し足りないかもしれません.
円柱座標は 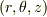 を採用しています.
|0f7f0c35b5d4f171f5f2f032b2f55d64|r|6472f20230b81c29ca9e27ba2dff3e88| とし,自分なりに調べた結果,静止座標系と回転座標系を考えて計算するのですが,正直混乱しています.
を採用しています.
|0f7f0c35b5d4f171f5f2f032b2f55d64|r|6472f20230b81c29ca9e27ba2dff3e88| とし,自分なりに調べた結果,静止座標系と回転座標系を考えて計算するのですが,正直混乱しています.
第1式は運動方程式を変形させたもので  はおっしゃる通り,
はおっしゃる通り,
 omega|39a1ea8c555bc288cff16c4aecfd88cd|v|cbb184dd8e05c9709e5dcaedaa0495cf|
です.したがって渦度の成分表示は
omega|39a1ea8c555bc288cff16c4aecfd88cd|v|cbb184dd8e05c9709e5dcaedaa0495cf|
です.したがって渦度の成分表示は
 omega|20d2c22257698df3bee30d388daaee91| の定ベクトルです.
第三式は発散の積分形のつもりです.計算する上で |0f7f0c35b5d4f171f5f2f032b2f55d64|n|cbb184dd8e05c9709e5dcaedaa0495cf| をおきました.この場合,回転座標系の単位ベクトルになるのでしょうか.
omega|20d2c22257698df3bee30d388daaee91| の定ベクトルです.
第三式は発散の積分形のつもりです.計算する上で |0f7f0c35b5d4f171f5f2f032b2f55d64|n|cbb184dd8e05c9709e5dcaedaa0495cf| をおきました.この場合,回転座標系の単位ベクトルになるのでしょうか.
速度場は |0f7f0c35b5d4f171f5f2f032b2f55d64|v|817b037d392597870e7ef646ee4a5525| のような形になると思います.答えになっていない部分が多くて申し訳ございません.
Re: 初めまして
りんご さんのレス (2007/01/11(Thu) 04:10)
>答えになっていない部分が多くて申し訳ございません.
これはお互い様ですので気楽にいきましょう.私も初めての問題な訳ですから,一緒に考えながら理解をしたいと思っています.むしろ,テツさんは私に対する問題説明者になっているのでしょうね.
今,風呂に入って頭がスキットしたので,コメントします.
>静止座標系と回転座標系を考えて計算する
恐らく,流体力学では「速度場」を扱っているので,我々は静止座標系のままでいいのだろうと思います.そもそもその為にラグランジェ微分というとんでもない怪物君の存在を許しているのですから.
で,速度場, 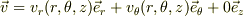 の係数のみが場の関数であり単位ベクトルは時間の偏微分の対象にならないのだろうと推測します(間違いでしたらご指摘ください→ご専門家の方々さま).なお,z方向の対称性から,これらの場の関数のz依存性は無視していいと思います.従って,以下では,zを省略します.
の係数のみが場の関数であり単位ベクトルは時間の偏微分の対象にならないのだろうと推測します(間違いでしたらご指摘ください→ご専門家の方々さま).なお,z方向の対称性から,これらの場の関数のz依存性は無視していいと思います.従って,以下では,zを省略します.
この座標系の回転を計算すれば,上記 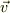 の成分の偏微分関数として与えられます.
の成分の偏微分関数として与えられます.
>第三式は発散の積分形のつもりです.
これは,半径rの円筒についてのベクトル場の面積分ですから,面の微小要素は 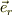 の方向を向き,
の方向を向き, 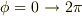 の範囲を積分すると考えればよいと思います.この積分では,
の範囲を積分すると考えればよいと思います.この積分では, 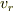 しか寄与しません.この成分は,あたかも線上の電荷が作り出す電場みたいに振る舞うようですね.
しか寄与しません.この成分は,あたかも線上の電荷が作り出す電場みたいに振る舞うようですね.
とすると,残りの 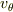 を運動方程式から求めるのが当面の課題です.
を運動方程式から求めるのが当面の課題です.
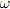 の時間依存性は,すこし検討が進んでから考えましょう.私は外側の壁が回転すると勘違いをしていましたが,中央のみが強制回転させられるのですよね.
の時間依存性は,すこし検討が進んでから考えましょう.私は外側の壁が回転すると勘違いをしていましたが,中央のみが強制回転させられるのですよね.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/11(Thu) 19:49)
えっと,問題が全然明瞭でないですが,このような問題でしょうか?
「
 軸に垂直で,間隔が単位長さの2枚の平行な平板に挟まれた「非」粘性非圧縮性流体の運動を考える.「
軸に垂直で,間隔が単位長さの2枚の平行な平板に挟まれた「非」粘性非圧縮性流体の運動を考える.「  軸」に流量が
軸」に流量が  である一様な線状のわき出しがあり,
である一様な線状のわき出しがあり,  方向に一様で軸対称定常な流れになっている.
これを
方向に一様で軸対称定常な流れになっている.
これを  軸まわりで角速度
軸まわりで角速度 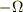 で回転する系から見たとき,
で回転する系から見たとき,  軸からの距離が
軸からの距離が  である位置における速度ベクトル
である位置における速度ベクトル 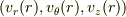 を求めよ.
」
これでは簡単すぎるかな?
を求めよ.
」
これでは簡単すぎるかな?
Re: 初めまして
テツ (大学3年) さんのレス (2007/01/11(Thu) 20:57)
りんごさん,toorisugari no Hiroさん,ありがとうございます. 問題の表記が自分よがりで申し訳ございませんでした. 概ねtoorisugari no Hiroさんのおっしゃるとおりです.
 軸に垂直で,間隔が単位長さ(非常に薄い?)の2枚の平行な円板にはさまれている粘性非圧縮流体(粘性流体です)の運動を考える.
軸に垂直で,間隔が単位長さ(非常に薄い?)の2枚の平行な円板にはさまれている粘性非圧縮流体(粘性流体です)の運動を考える.  軸に流量が
軸に流量が  である湧き出しがあり,
である湧き出しがあり,  方向に一様で軸対象定常な流れになっている.円盤は
方向に一様で軸対象定常な流れになっている.円盤は  軸まわりで角速度
軸まわりで角速度  で運動している.このときの速度ベクトル
で運動している.このときの速度ベクトル  を求めよ.
ただし遠心力は考えなくてよい.円盤の半径は
を求めよ.
ただし遠心力は考えなくてよい.円盤の半径は  とする.
とする.
という問題です.toorisugari no Hiroさん,ご指摘ありがとうございました.
りんごさん,問題が不鮮明な部分が多々あり,その上でのアドバイス,大変ありがたく思います.当方電磁気の知識はあまりありませんが,アプローチのひとつとしてちょっと調べて考えてみます. 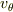 がこの問題のキーポイントですね.
がこの問題のキーポイントですね.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/11(Thu) 21:14)
> 「軸に垂直で,間隔が単位長さ(非常に薄い?)の2枚の平行な円板にはさまれている粘性非圧縮流体(粘性流体です)の運動を考える.z軸に流量がQである湧き出しがあり,z方向に一様で軸対象定常な流れになっている.円盤はz軸まわりで角速度omegaで運動している.このときの速度ベクトルvを求めよ.ただし遠心力は考えなくてよい.円盤の半径はaとする.」
えっと,この問題はおかしいです.粘性流体ならz方向に一様はありえません.(境界付近では円盤に対して流体が静止していることになるので,剛体回転してる事になりますが,これではわき出しと矛盾します.)
「  軸に垂直で,間隔が単位長さの2枚の平行な円板にはさまれている動粘性率が
軸に垂直で,間隔が単位長さの2枚の平行な円板にはさまれている動粘性率が  の粘性非圧縮流体の運動を考える.
の粘性非圧縮流体の運動を考える.  軸に流量が
軸に流量が  である湧き出しがあり,軸対称定常な流れになっている.軸から十分に離れたところ(
である湧き出しがあり,軸対称定常な流れになっている.軸から十分に離れたところ( 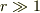 )では流れは
)では流れは  軸に垂直になると考え,このときの速度ベクトル
軸に垂直になると考え,このときの速度ベクトル  を求めよ.」
を求めよ.」
の解答をすでにご存じなら上の問題(  一様性ははずす)も解けるかもしれませんが,下の問題もかなり難しい(解けるかどうかもわかりません)ので,3回生レベルではないと思います.
一様性ははずす)も解けるかもしれませんが,下の問題もかなり難しい(解けるかどうかもわかりません)ので,3回生レベルではないと思います.
Re: 初めまして
テツ (大学3年) さんのレス (2007/01/11(Thu) 21:30)
toorisugari no Hiroさんご指摘ありがとうございます.
下の問題です.湧き出し(  軸)から十分に離れたところと考えた方がよいのでしょうか?円の外は吸い込みと考えてよいようです.
軸)から十分に離れたところと考えた方がよいのでしょうか?円の外は吸い込みと考えてよいようです.
上記3式を連立させて計算と考えたのですが,これでは無理なんでしょうか.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/11(Thu) 21:36)
> 下の問題です.湧き出し(z軸)から十分に離れたところと考えた方がよいのでしょうか?円の外は吸い込みと考えてよいようです.
だって,速度場は  方向に非一様であるために,中心に近いところでは
方向に非一様であるために,中心に近いところでは  方向(
方向( 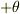 方向)の速度成分も考えなければいけません.純然たる3次元問題なんて簡単に解けません.
方向)の速度成分も考えなければいけません.純然たる3次元問題なんて簡単に解けません.
ただし,  方向に平均を取った速度を考えるのなら下の問題は3回生でも解けます.しかし,上の問題(
方向に平均を取った速度を考えるのなら下の問題は3回生でも解けます.しかし,上の問題(  一様性は仮定しない)はそれでも解けるかどうかわかりません.解けるのなら,たぶん,私が最初に出した問題と本質的に同じになるはずです.(中心軸に近いところではズレがありますが...)
一様性は仮定しない)はそれでも解けるかどうかわかりません.解けるのなら,たぶん,私が最初に出した問題と本質的に同じになるはずです.(中心軸に近いところではズレがありますが...)
Re: 初めまして
りんご さんのレス (2007/01/11(Thu) 21:42)
境界条件がここまでシビア(上下円盤,半径aの外壁)ともなると,境界層もチキンと解析に入れて,なおかつ一種の対流も起こさないといけないようですね.
これは,素人が下手な論議をすると混乱の基ですので,私はスペクテイタとして拝見したいと思います.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/11(Thu) 21:48)
> 上記3式を連立させて計算と考えたのですが,これでは無理なんでしょうか.
いまのままでは,労力の無駄だと思います.正しい問題をもう一度先生に聞かれることをおすすめします.
Re: 初めまして
テツ (大学3年) さんのレス (2007/01/11(Thu) 21:48)
>速度場は方向に非一様であるために,中心に近いところでは方向の速度成分も考えなければいけません.純然たる3次元問題なんて簡単に解けません.
 方向の速度を考えていませんでした.確かにこのままでは自分では手に追いそうなレベルではないです.
方向の速度を考えていませんでした.確かにこのままでは自分では手に追いそうなレベルではないです.
 軸上に湧き出しの点源があり,
軸上に湧き出しの点源があり,  方向には速度が無い
方向には速度が無い
と修正お願いします.
りんごさん
円盤の半径は  で外壁はないです.
で外壁はないです.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/11(Thu) 21:59)
> 境界条件がここまでシビア(上下円盤,半径aの外壁)ともなると,境界層もチキンと解析に入れて,なおかつ一種の対流も起こさないといけないようですね.
たぶん,以前,ティーカップの話題でものぼったエックマン境界層とかを(中心軸に近いところでは)考えなければいけないのかもしれませんね.(十分遠方になると普通の平板流れに近くなると思いますが...)
Re: 初めまして
りんご さんのレス (2007/01/11(Thu) 22:35)
テツさん,
>z軸上に湧き出しの点源があり,z方向には速度が無い >円盤の半径はaで外壁はないです.
これは,大きな水槽の中に同心の2円盤が水没していて,中心軸(z)の周りを,ある時刻から一定速度で回転を初めて,かつ,2円盤の軸中心の中央(座標原点)に湧き出しの点源がある;
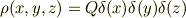
という事ですか?
円盤と挟まれた流体の間は境界層ですますとして,円盤の外側の水はどのような境界条件を付与するのでしょうか?
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/11(Thu) 22:42)
先生に聞き直すのをおすすめします.
> z軸上に湧き出しの点源があり,z方向には速度が無い
これでも簡単ではないですよ.z方向の非一様性は速度の大きさが変化するだけでなく,速度の方向も,zに対して(  方向に)変化することを意味してるのですから.(何か,さらに仮定をいれれば,解けるかもしれませんが,それより先生に相談してください.)
方向に)変化することを意味してるのですから.(何か,さらに仮定をいれれば,解けるかもしれませんが,それより先生に相談してください.)
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/11(Thu) 22:45)
> 円盤と挟まれた流体の間は境界層ですますとして,円盤の外側の水はどのような境界条件を付与するのでしょうか?
板を無限に大きいとすれば余計なことを考えなくてもいいと思います.
Re: 初めまして
りんご さんのレス (2007/01/11(Thu) 22:51)
今少し前に投稿してから,急に気になりだしました.
もし,良かったら問題をそのまま書き下すとどうなるかなとおもいました.
toorisugari no Hiroさんもそうだろうと推察しますが,この問題は物理の学生さんに出す問題としては,難しすぎるように感じました.で,私としては,ちょっと納得いかないように思います.
問題が整理できたら,ぜひともまた書き込んでください.今回のスレッドのおかげで,渦度の式が少し身近になったようです.2次元の場合を,複素関数論と組み合わせて,遊んでみようと思えるようになりました.こんなチャンスをくださり,有り難うございました.
Re: 初めまして
テツ (大学3年) さんのレス (2007/01/11(Thu) 23:03)
Z軸が非常に薄い円柱の容器があり,円の中心(Z軸)に湧き出しがあります.円の外側は吸い込み(あふれるというニュアンスでしょうか)の条件で円柱をZ軸まわりで角速度  で円柱を回転させたらどうなるか
で円柱を回転させたらどうなるか
とういうイメージをしています.toorisugari no Hiroのおっしゃられた通り,今考えている円柱の底辺から湧き出しということになると,3次元の問題になり,自分では手に負えない問題となってしまうので円柱の表面の点源から湧き出ると考えてます.なので原点は特異点のような考えでした.流体の隆起などはまだそこまで教わっていないので考えなくてよいと思っていたのですが,この条件では考えなくてはいけないのでしょうか・・.出題者が情けなくてすみません.
toorisugari no Hiroさん,助言ありがとうございます.境界層などといったこれから教わるであろうことに触れることができました.このまま悩んでもらちがあかなそうなので,一度先生に聞いてきます.
りんごさんもありがとうございました.おかげで条件を見つめなおす機会ができました.一度頭の中を整理しなおしてみます. お二方,どうもありがとうございました.
Re: 初めまして
りんご さんのレス (2007/01/12(Fri) 02:52)
電磁気からの類推+α
同心円筒は,電場でも磁場でもあり得る設定ですね.ただこれらでは,円筒はまず静止したままですが.
さて,2重の同心円筒を考え,内径をa,bとし,円筒の中心はz軸に一致しているとします.その長さをLとし,その中点が z=0に一致しているとします.
Δz=1の長さについて,円筒aの表面積(2πaΔz)からQΔzのわき出しがあるとし,円筒bの内側表面ではQΔzの吸い込みがあるとします.このイメージは同軸のコンデンサのイメージ,2次元の電場の感じに似ていますね.
次に,円筒bをある時刻から一定の角速度で回転するとします.当然その回転に引き連れられて,外から中心に向かいながら接戦方向の速度場が形成されますね.このイメージは電磁気には直接の類似は在りませんが,電流分布を同径方向の関数として付与して行くときの磁場みたいなイメージに近いとおもいます.
なお,これらに於いて,a<b<<Lといった幾何学的条件を付与すれば,z方向の速度は無視しできるような気がします.
Re: 初めまして
yama さんのレス (2007/01/12(Fri) 13:48)
りんごさんのイメージで円筒aの半径を限りなく小さくしていけば,z軸から湧き出すと考えてよいのではないでしょうか. つまり,点源からではなく,線源から湧き出すということです. 結局,りんごさんが初めに書かれた「無限に長い直径がゼロの電流がつくる磁場」のようなイメージになりそうですね.
Re: 初めまして
りんご さんのレス (2007/01/12(Fri) 22:04)
どうも流体力学というと,何となく無限大とか無限小という記述に抵抗をかんじます.
でも,yamaさんの割り切り方を拝見していると,無限大を認めてしまえば,外側の円筒を外してしまうのもありかと思いました.
ただ,逆に内側の円筒の径を極限まで小さくすると 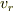 が発散するようで,この解釈が気になるところです.
が発散するようで,この解釈が気になるところです.
以上の問題点を一先ず於いておくと,運動方程式は意外に簡単になり「拡散の方程式+アルファ」という感じになりそうですが, 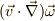 の処理がまだ良くわかりません.
の処理がまだ良くわかりません.
#なお,解には, 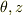 への依存性がないことを仮定しました.
への依存性がないことを仮定しました.
具体的な解を得るところは,テツさんにお任せした方が早いかと思います(笑).
なお,一般に,「ベクトルとナブラの内積」の円筒座標系での正しい表現をご存知でしたら教えてくださいませんか?意外と,勾配,発散,回転までは書いてあっても,これまで書いてない...,今まで自分も,それで満足していた一人ですが,これで流体の計算を始めている実感を得たように感じます.
Re: 初めまして
りんご さんのレス (2007/01/12(Fri) 22:56)
本能的に「ナブラの外積」には恐怖心が働くのですが...,状況によっては素直な挙動をすることを期待して,検討させていただきます.:)
すこし計算しました.対称性が高い場合は回転をしても,項目が増えないのがいいですね.しかし,電磁気などと違って,出てくる項の数が多いので,数学ソフトでも使わない事には,検算だけでも気が滅入ります.
今頃気がつきましたが,  には,
には, 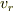 が入っていない!うまい事,速度場の発散と渦場が方程式上も事前に分離しているかのようですね.対称性万歳.
が入っていない!うまい事,速度場の発散と渦場が方程式上も事前に分離しているかのようですね.対称性万歳.
Re: 初めまして
yama さんのレス (2007/01/12(Fri) 23:53)
「ベクトルとナブラの内積」は,ベクトル 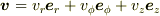 と
と 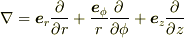 の内積なので,次のようになると思います.
の内積なので,次のようになると思います.
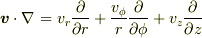 流体力学の本にのっている円筒座標系での方程式においてもこのように表されているようです.
流体力学の本にのっている円筒座標系での方程式においてもこのように表されているようです.
Re: 初めまして
りんご さんのレス (2007/01/13(Sat) 02:03)
yamaさん,
こういう基本が判らなくなったのは,老害の一つかもしれません.
先のtoorisugari no Hiroさんの3重積方式とクロスチェックしてみます.
Re: 初めまして
zoro さんのレス (2007/01/13(Sat) 11:28)
toorisugari no Hiroさん,
>「座標変換するなら」
これって, (x,y,z)座標で計算しておいて,微分方程式が得られたら,(x,y)対称性を考慮して,x=0でのyの挙動を考えるとかいった技法ですか?
慣れない計算をするためには,なるべく多くの計算をしてクロスチェックをしたいですよね.
Re: 初めまして
りんご さんのレス (2007/01/15(Mon) 03:24)
結局,円筒座標でのヴェクタ解析の復習に時間を費やしましたが(泣),渦度場の運動方程式としては,
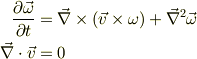
ただし,円筒からの涌出・円筒の回転に流体が静止の境界条件は省略.
速度場として
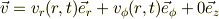
を仮定すると,渦度場,  はz成分しか持てなくて,
はz成分しか持てなくて,
![\vec \omega &= \omega(r,t)\vec e_{z}\\\omega(r,t) &= \frac{1}{r}\frac{\partial [r v_{\phi}(r,t)]}{\partial r}](http://hooktail.maxwell.jp/bbslog/0a5c05e8d37675399665733918ce6019.png)
具体的に解こうとすると,非線形項(コリオリ力みたいに見えますね);
![\vec \nabla \times (\vec v \times \vec \omega ) = \frac{1}{r}\frac{\partial}{\partial r}[r\omega(v_{\phi}-v_{r})]\vec e_z](http://hooktail.maxwell.jp/bbslog/ba05f3f2510f9563b048b0154878fad5.png)
をどこまで取り込むかが鍵になりそうですね.
以上の添削をお願い致します.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/15(Mon) 16:58)
支配方程式は
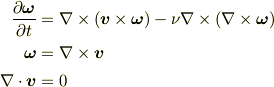
ですね.
今ここで 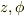 依存性は無視できるとし,さらに
依存性は無視できるとし,さらに 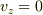 とすると
とすると
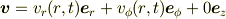
となります.
ここで,
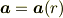
に対して
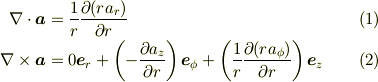
という公式を使うと,
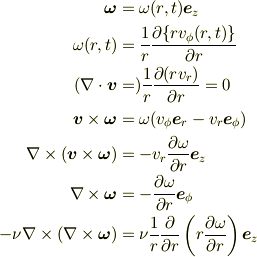
ですから,方程式は
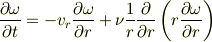
となりますね.
あとこれに,
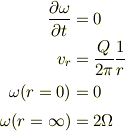
と言う条件を加えれば解けないかな?
#でも,本当は  依存性は入れた方がよいと思う.
依存性は入れた方がよいと思う.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/15(Mon) 17:44)
> ですから,方程式は >
> となりますね.
> あとこれに, >
> と言う条件を加えれば解けないかな?
どうも上の解は存在しなそうですね.( 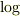 の二次多項式.)
定常解ではダメと言うことは....面倒くさそう...
の二次多項式.)
定常解ではダメと言うことは....面倒くさそう...
Re: 初めまして
りんご さんのレス (2007/01/15(Mon) 19:13)
toorisugari no Hiroさん,
詳しい計算過程のご教示,有り難うございます.まだ不慣れな為に,符号が判らなくなったり,基底を間違えたりしています.とくにいま教科書にしている神部さんの流体力学の円筒座標は 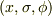 で,今使っている座標でいえば,
で,今使っている座標でいえば, 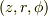 で,一時は大混乱になりました(笑).
で,一時は大混乱になりました(笑).
さて,今ひとつ判らないのは, 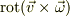 がかなりシンプルになっているところです.式の変形をお教えくださいますか?
がかなりシンプルになっているところです.式の変形をお教えくださいますか?
>> あとこれに, >
> と言う条件を加えれば解けないかな?
境界条件の付け方ですが,動径方向の速度 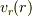 が円筒(半径a)の表面からの涌出で決まる事から,このさい運動方程式では与えられた関数としてしまおうと思います.
が円筒(半径a)の表面からの涌出で決まる事から,このさい運動方程式では与えられた関数としてしまおうと思います.
また,回転運動の付与は,上記の円筒(半径a)を強制的に回転し,その表面に粘性流体が付着すると考えたいところです;
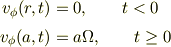
この接線方向の速度は,イメージでは,静止した水飴に棒を突っ込んで,t=0から回転させると,だんだんに内側の回転が外側に伝わっていくように推察しています.
ですから当面は,時間の依存性をなんとかキープしたいと思います.
なお,z依存性の件ですが,電磁気学でも「解放端」の処理はいつも内在している訳ですよね.特に,現実問題とすぐに向き合う場合には重要でしょう.しかし,物理の問題を解くときに,その問題点を知った上で,問題を簡略化,理想化する訓練も大事だと思います.その意味で,
・無限大近似 →+ーz方向の対称性→z方向依存性の無視可能の認識
といった直感力を育てる事が必要に思います.もちろん,「解放端」問題は,中級の流体力学や電磁気,解析力学で論じていただきたく思います.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/15(Mon) 20:44)
> さて,今ひとつ判らないのは, 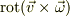 がかなりシンプルになっているところです.式の変形をお教えくださいますか?
がかなりシンプルになっているところです.式の変形をお教えくださいますか?
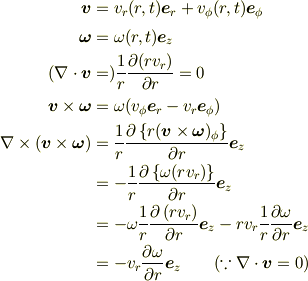
です.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/15(Mon) 21:04)
結局  依存性をいれなければ,
「
依存性をいれなければ,
「
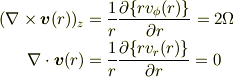
となる, 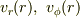 をもとめなさい.(
をもとめなさい.( 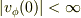 )」
という問題以上のことはできないのではないでしょうか.時間依存性を入れても意味ないような気がします.
)」
という問題以上のことはできないのではないでしょうか.時間依存性を入れても意味ないような気がします.
Re: 初めまして
りんご さんのレス (2007/01/15(Mon) 21:15)
toorisugari no Hiroさん,
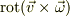 の件,判りました,お恥ずかしいです.やはり一度公式と図は自分で作らないて駄目そうですね.
の件,判りました,お恥ずかしいです.やはり一度公式と図は自分で作らないて駄目そうですね.
御蔭さまで,渦度場の運動方程式は一揃いできたので,少し考えてみます.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/16(Tue) 20:50)
zoroさん 見逃してしまい,返事し損なってました._o_
>>「座標変換するなら」 > これって, (x,y,z)座標で計算しておいて,微分方程式が得られたら,(x,y)対称性を考慮して,x=0でのyの挙動を考えるとかいった技法ですか?
座標変換するときはベクトル解析的に素性のよい形(rot,grad,divおよび,純粋なベクトルの内積・外積)で表現した方が間違いがないからです.
今回のは幸いにも,スカラー渦度方程式で他の方法で解いても結果は同じですが,一般には付加項がつくことがあるので,用心した方がいいです. (たとえば加速度項
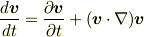
は座標変換した成分表示で慣性力項(遠心力など)が現れるのですが,そのまま,例えば, 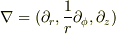 により,
により,
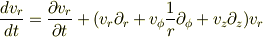
とすると,慣性力項が現れませんのでおかしいことになります.)
( 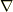 を共変微分と考えれば間違いはないのですが....)
を共変微分と考えれば間違いはないのですが....)
Re: 初めまして
zoro さんのレス (2007/01/16(Tue) 21:46)
toorisugari no Hiroさん,
とても詳しいご解説有難うございました.渦の場を具体的に論議されていて,とても興味深く拝見しています.
ひょっとして,動径方向だけだから,デカルト座標のままと同じかと思ってしまいました.そんな巧い話はないですよね.
>∇を共変微分で考えれば間違いはないのですが....
この方法は知らないのですが,簡単にわかる様なものですか? もし一言で解説が出来なければ,ご無理は申しません.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/16(Tue) 22:00)
>> 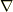 を共変微分で考えれば間違いはないのですが....
> この方法は知らないのですが,簡単にわかる様なものですか?
を共変微分で考えれば間違いはないのですが....
> この方法は知らないのですが,簡単にわかる様なものですか?
ニュートンの運動方程式を軸座標表示すると慣性力の項があらわれますよね.
それは 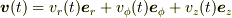 を時間微分するとき基底の時間微分
を時間微分するとき基底の時間微分
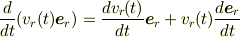
を考えなければいけないためですよね.
同様に 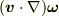 についても基底の空間微分を考えなければいけないと言うことです.それを含めたものが共変微分ですよね.
についても基底の空間微分を考えなければいけないと言うことです.それを含めたものが共変微分ですよね.
ただこれは面倒なので,幾何学的にきれいな形にして,回避すると言うが定石だと思います.
Re: 初めまして
zoro さんのレス (2007/01/16(Tue) 22:22)
なるほど,通常の「古典力学にでてくる粒子の運動」を考える時の「極座標」とか「円筒座標」とかに出てくる「基底」は,運動粒子に固定されている為に方向が時間依存性をもちますね.
しかし,通常の「流体力学に出てくる微小体積素にある流体部分の運動」を考える時には,微小体積素の運動は「速度場」によって支配されていて,「基底」は速度場のそとに静止しているように解釈したくなります.
実は,今回の論議の中でもチラホラと論議があり,この解釈を厳密に理解できたら嬉しいと思いました.急ぎませんが,この点につて時間の許すなかで解説いただけると有り難いです.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/16(Tue) 22:47)
> 「基底」は,運動粒子に固定されている為に方向が時間依存性をもちますね. > 「基底」は速度場のそとに静止しているように解釈したくなります.
えっと,基底は空間の各点に対して定義されているので,粒子が動いたときのベクトルの成分の変化をみる(時間微分)事も,異なる点におけるベクトルの成分を比較する(空間微分)事も,基底の変化を考慮に入れないとダメと言う意味では同じだと思うのですが...
Re: 初めまして
zoro さんのレス (2007/01/16(Tue) 23:32)
つい興味に負けて,素人質問をしてしまいましたが,素人論議を続けさせていただきます.破綻したら御免なさい.
簡単の為に,2次元の極座標で,原点からの距離r,x軸からの半時計方向にφとします.
古典粒子:
ある時刻tに見出した粒子と共に運動する視点を取る.
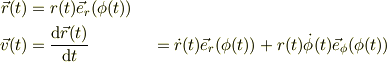
速度場の微小体積素:
橋の上から,ある時刻tに,流体のどこの体積素を観察するかを決める = 「tと, rとφと」を決める.
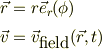
加速度になると,恐怖の移動項がでてきて....
勿論,流体系を容器もろとも回転させるとか,地球の自転を考える時は,流体系のフレームそのものの運動が与えられるので,それはコリオリ・フォースと類似の処理になるわけですよね.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/17(Wed) 00:01)
ごめんなさい.まだ質問の意図がつかめません.もう少し説明してもらえませんか?
# 粒子描像と場の描像を混同されている気がします.
Re: 初めまして
zoro さんのレス (2007/01/17(Wed) 00:42)
>まだ質問の意図がつかめません.もう少し説明してもらえませんか?
再度検討してみます.
逆に,ご確認したいのは,
>基底の空間微分を考えなければいけない
ですが,おそらく 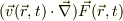 と言う場合,裸の微分演算子がヴェクタFに作用しているので,基底も角度の偏微分を受けるので,忘れないことと理解しましたが,宜しいでしょうか.
と言う場合,裸の微分演算子がヴェクタFに作用しているので,基底も角度の偏微分を受けるので,忘れないことと理解しましたが,宜しいでしょうか.
今頃気が付きましたが,「 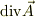 」と「∇の定義と単純にヴェクタAと内積した」とでは違うのですね.
」と「∇の定義と単純にヴェクタAと内積した」とでは違うのですね.
恐らく問題点の解釈が伸展始めた様ですが,もうしばらく検討してみたいと思います.
以上までのご教示に感謝します.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/17(Wed) 15:43)
> 「基底」は,運動粒子に固定されている為に方向が時間依存性をもちますね.
>
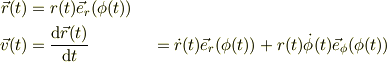
ここを誤解されているのかもしれません. 基底は運動粒子に固定されていません.粒子と基底は無関係です(今,moving frameは考えないでください.:-))
また,位置は本来ベクトルではありません.点です.点と点を結んで初めてベクトルが作られます.
ベクトルは接空間の元であり,本来の空間の元ではないと考えた方がいいと思います.(幸か不幸か我々の世界はユークリッド空間なので,接空間で作ったベクトルを位置(ベクトル!?)にまで「乱用」できてしまいますが...)
ですから,基底は位置を微分した速度に対して適用する概念であり,位置に適用する概念ではありません.
Re: 初めまして
zoro さんのレス (2007/01/17(Wed) 17:10)
>基底は運動粒子に固定されていません.粒子と基底は無関係です(moving frameは考えないでください.)
としたら,位置ヴェクタ,速度ヴェクタをどの様に表現し,どの様に解釈すれば良いかを具体的にお教えくださいますか?
これに関連して,私は,円筒座標系や極座標系で運動を記述するということは,本質的に非慣性系で運動を記述することと理解してきました.そうでないと,少なくとも私は,遠心力やコリオリの力を容易に理解できなくなります.
力学の初歩の疑問で申し訳ありませんが,素人向けにレビューいただけると幸いです.でも,流体での加速度運動との対比の上で,重要な点と思います.
>また,位置は本来ベクトルではありません.点です.点と点を結んで初めてベクトルが作られます.
数学ではどのように考えるのか知りませんが,少なくとも古典物理学の範疇では,ある慣性系を考えて,そこに座標原点をとり,その原点から考察する運動物体の点を連結する矢印として,位置ベクタを認識すると思います.
余程のことが無い限り,古典物理の扱う空間はデカルト座標で記述できるユークリッド空間であって,空間は一様でゆがみの無いものと思っています.また「ベクトルは接空間の元」といった高度の概念を引用されても,なんとも理解できません.もし宜しければ,数学的素養のない事を前提にご解説いただけると幸いです.
もっとも,あまりにも手間が掛かりすぎるとお考えでしたら,参考文献をお教えいただければと思います.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/17(Wed) 18:20)
えっと直前の質問はしばらく考えさせてください.
> 今頃気が付きましたが,「 |aa755a0fbb74f1e0a85301adea38f56f| 」と「 |8319f01cae0e5752ba2e719544659959| の定義と単純にヴェクタAと内積した」とでは違うのですね.
そうです.軸座標系などでは,divを 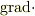 と考えない方がよいですね.
なぜなら基底の発散も考慮しなければいけないからです.
と考えない方がよいですね.
なぜなら基底の発散も考慮しなければいけないからです.
(以下蛇足.ちょっと難解かも)
なお,正規直交基底をすてて自然基底でかんがえれば,「 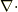 と考え」てよいです.
と考え」てよいです.
以下では 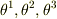 で表される曲線座標系において,基底として
で表される曲線座標系において,基底として 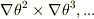 (管ベクトルの基底)をつかっています.
(管ベクトルの基底)をつかっています.

(1)が味噌です.なお,最終式ではスカラー三重積の性質を使っています.
また, 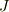 は
は 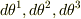 から作られる平行6面体の体積要素で,
から作られる平行6面体の体積要素で, 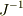 は「密度の基底」です.
は「密度の基底」です.
なお,ここで,
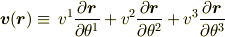
とするなら( 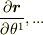 が(接ベクトルの)基底)
が(接ベクトルの)基底)
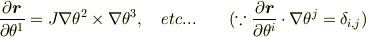
なので 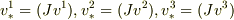 ,つまり,
,つまり,
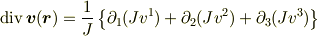
が得られます.
デカルト座標系では, 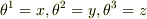 より
より
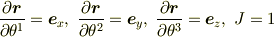
軸座標系では, 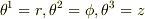 より
より
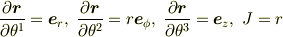
を考慮すれば通常の成分表示
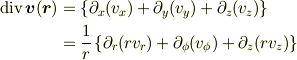
が得られます.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/17(Wed) 20:25)
> としたら,位置ヴェクタ,速度ヴェクタをどの様に表現し,どの様に解釈すれば良いかを具体的にお教えくださいますか?
>> 位置は本来ベクトルではありません.点です.点と点を結んで初めてベクトルが作られます. > 数学ではどのように考えるのか知りませんが,少なくとも古典物理学の範疇では,ある慣性系を考えて,そこに座標原点をとり,その原点から考察する運動物体の点を連結する矢印として,位置ベクタを認識すると思います.
位置ベクトルは厳密にはベクトルではありません.
点 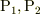 を表す位置ベクトル
を表す位置ベクトル 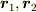 を考えるとしましょう.ベクトルには加算とスカラー倍が定義されます.加算
を考えるとしましょう.ベクトルには加算とスカラー倍が定義されます.加算 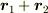 を形式的には計算できますが,意味を持ちません.(「点
を形式的には計算できますが,意味を持ちません.(「点 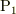 と点
と点 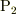 を加えたもの」に何の意味がありますか?)
でも,差には意味があります.そしてこれがベクトル(
を加えたもの」に何の意味がありますか?)
でも,差には意味があります.そしてこれがベクトル( 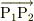 )です.(あと,中点等の,直線
)です.(あと,中点等の,直線 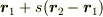 上の点は意味がありますが,これは蛇足です.)
上の点は意味がありますが,これは蛇足です.)
物理的に考えても同様です.粒子は「観測者」によらず存在しているはずです.つまり原点をどこにとるかは「粒子がある位置にいる」こととは関係ないはずです.位置ベクトルは原点を必要とします.これは物理的に考えても不純です.
(だからといって,位置ベクトルの使用を禁止しているわけではありません.念のため.)
どうせ不純なら,原点だけ与えるのでなく,空間メッシュ(格子)=曲線座標系も与えるべきだと思います. つまり,位置は
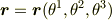
と書くのがよいですし,成分表示など,これ以上書くものではありません.
(ま,現実には「暗黙のデカルト座標系」で成分表示しないと関数を記述できませんが,曲線座標系の基底で位置ベクトルの成分表示する訳ではないですよね.)
(なお,点を 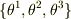 と表すことはできますが,これは位置ベクトルの成分表示ではないことに注意すべきです.)
と表すことはできますが,これは位置ベクトルの成分表示ではないことに注意すべきです.)
でも速度は
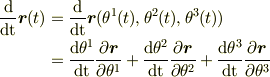
となるので,自然にベクトル成分表示ができます.( 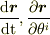 は位置の差のスカラー倍(=ベクトル)であることに注意)
は位置の差のスカラー倍(=ベクトル)であることに注意)
自然基底( 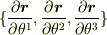 )では
)では
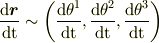
(これはベクトルの成分表示ですが,上の 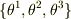 を時間微分したものではありません.)
を時間微分したものではありません.)
曲線直交座標系における正規直交基底(
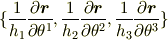
)では(ただし, 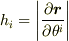 )
)
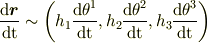
とできます.
なお,基底は速度から定義されると考えるのではなく,微分
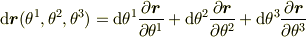
で定義されるものです.そして 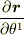 は,
は, 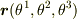 に対して
に対して 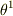 だけを変化させてできる,曲線の接線に平行ですから「接ベクトルの基底」と呼びます.
だけを変化させてできる,曲線の接線に平行ですから「接ベクトルの基底」と呼びます.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/17(Wed) 22:12)
書き込みラッシュになってすいません.> みなさま
> これに関連して,私は,円筒座標系や極座標系で運動を記述するということは,本質的に非慣性系で運動を記述することと理解してきました.そうでないと,少なくとも私は,遠心力やコリオリの力を容易に理解できなくなります.
慣性力と「曲線座標系表示における時間微分の付加項」とは物理的には同値ではありません.曲線座標系をとっても非慣性系にならないので,付加項は慣性力ではありません.ただ,私も先の記事で「慣性力項」というミスリーディングな言い方をしてるので,何ですが...
結論から言えば,成分表示が悪いのです.物理的実体はベクトルそのものであって,成分のような「数字の組」ではありません.速度ベクトルについては時間微分も「さらっ」と問題なくかけます. しかし,成分で考えるときには「基底の時間微分」の寄与を含めなければいけず,単純な「成分の時間微分」にはなりません.
この付与項を拡大解釈的に「慣性力項」とよんでますが,これは非慣性系の慣性力とは「狭い意味で」関係ありません.単に成分で見てるから見かけの付与項ができたためです.実体である加速度ベクトルは定義のままの 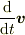 ですから.
ですから.
今,うまく表現できませんが,真の慣性力は座標系の取り方自体が時刻に依存していることから発生するのだと思います. (あるいは位置ベクトルの基準である原点が時刻に依存していると言い換えてもいいです.あ,でもこれだとコリオリ力を説明できませんね.;-))
真の慣性力とは,位置ベクトルの2階時間微分 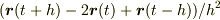 を採るときに,比べる3つの位置ベクトルが視点が動くせいで正しい組になっていないので,位置ベクトルの2階時間微分についてしまう付加項
を採るときに,比べる3つの位置ベクトルが視点が動くせいで正しい組になっていないので,位置ベクトルの2階時間微分についてしまう付加項 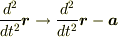 である,と言う解釈が正しいかな?
である,と言う解釈が正しいかな?
Re: 初めまして
zoro さんのレス (2007/01/17(Wed) 23:32)
No.13751の基底のご解説は難しいので,下記のご解説を読んでいます.
No.13752に於いて;
>位置ベクトルは厳密にはベクトルではありません.
>点 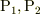 を表す位置ベクトル
を表す位置ベクトル 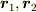 を考えるとしましょう.ベクトルには加算とスカラー倍が定義されます.加算
を考えるとしましょう.ベクトルには加算とスカラー倍が定義されます.加算 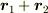 を形式的には計算できますが,意味を持ちません.(「点
を形式的には計算できますが,意味を持ちません.(「点 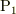 と点
と点 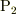 を加えたもの」に何の意味がありますか?)
を加えたもの」に何の意味がありますか?)
剛体の重心ヴェクタは「位置ヴェクタの重み付き総和ヴェクトルを全体重みで規格化したヴェクタ」と思いますが,それが物理的に意味が無いのなら,力学を計算できなくなってしまうような.
私は,細かな計算はフォローできても,基底の定義が無いままに論議が進行できるのが,高校生の頃からの不安でした.大学のベクトル解析に期待したのですがわからず,高木さんの解析概論は頭に入らず,その後,基底に関する疑問(それに付随して,面積た体積の認識)を封印して長い時間がたちました.
で核心に近付いたと思えるのは, ーーー引用ーーー 位置は
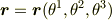
以上書きようがありません.点を 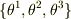 と表すことはできますが,これは位置ベクトルの成分表示ではありませんね.
ーーー引用ーーー
と表すことはできますが,これは位置ベクトルの成分表示ではありませんね.
ーーー引用ーーー
この記述を,私は全く理解できないのです.自分の目には,我々が存在する空間を指し示す為に,3つのパラメータが居ることは判ります;
例えば,3つの別々の物差しを先ず,一つに束ねて,其々が同一であることを確認した後に,あるダンボール箱の一つの隅を原点として,其々の稜に沿って物差しを固定して,空間の1点を指し示す事は理解できます.
しかし,この「物差しの示す値」, 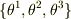 ,だけで,空間の指定は出来ません.ダンボールという幾何学的構築物があってこその物差し値が意味あるとしか思えません.
,だけで,空間の指定は出来ません.ダンボールという幾何学的構築物があってこその物差し値が意味あるとしか思えません.
もし,「物差しの示す値」からのみ演繹的にダンボールの役割を説明できるのでしょうか? もし,それが可能ならとても嬉しく思います.
No.13754に於いて
ほとんど,私の理解の向こう側にあるようです.私は「幾らヴェクタ記号だけを拝見しただけでは,その物理的な解釈が出来る」とは思えません.
====
もともと,テツ(大学3年)さんが, 2007/01/11(Thu) 03:00 No.13650のページで
>自分なりに調べた結果,静止座標系と回転座標系を考えて計算するのですが,正直混乱しています.
と発言されていて,私もその点が知りたかったのです.
当面は,冒頭にお示しした具体例を元に,自分なりに勉強したいと思います.
皆様,とんだ横滑りの質問をして済みませんでした. m(_._)m
Re: 初めまして
MXK さんのレス (2007/01/18(Thu) 00:05)
toorisugari no Hiroさん
note (1)の 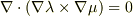 は座標のメッシュがつくる管の性質ですね.
は座標のメッシュがつくる管の性質ですね.
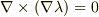 を引き継いでいるのですね.
を引き継いでいるのですね.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/18(Thu) 00:19)
> No.13751の基底のご解説は難しいので,下記のご解説を読んでいます.
あ,これは良い解説ですね.参考にします.ざっと読みましたが,そう違うことは言ってないので,このページで理解されれば良いと思います.
> 剛体の重心ヴェクタは「位置ヴェクタの重み付き総和ヴェクトルを全体重みで規格化したヴェクタ」と思いますが,それが物理的に意味が無いのなら,力学を計算できなくなってしまうような.
鋭い返しですね.:-)
重心の位置ベクトル 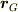 の定義は
の定義は
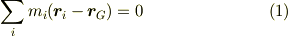
です.これにより,
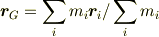
- となるだけで,和を採ることの正当性(意味)は(1)の段階(変位ベクトルの和)で保証されています.(冗長な記述は消しました.)
> しかし,この「物差しの示す値」,{theta^1,theta^2,theta^3},だけで,空間の指定は出来ません.ダンボールという幾何学的構築物があってこその物差し値が意味あるとしか思えません.
えっと,私はメッシュ(格子)を導入すると書きました. 空間に網目模様を書き,原点を決め,網目の面を構成する曲面の方程式を決めることが座標系を設定する事になります.(軸座標系なら,中心軸からの同心円(管)の「群」,中心軸からいろいろな方向へ放射する面の「群」,等高面の「群」によって格子ができますね.)
メッシュ(格子)を書くと網目模様になりますが,その網目を構成している(3次元だから)曲面は 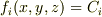 で与えられます.(軸座標系なら,
で与えられます.(軸座標系なら, 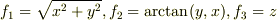 です).三つの曲面
です).三つの曲面 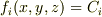 の交点は
の交点は
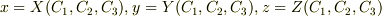 となりますが(軸座標系なら,
となりますが(軸座標系なら, 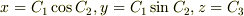 です),これが曲線座標系表示に他なりません.
です),これが曲線座標系表示に他なりません.
このとき格子の面の間隔が物差しの幅ですが,ダンボールは格子そのものです. 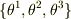 とは3本の物差しを用意するだけでなく,おのおのの点で物差しをどの角度に当てるかもすでに指定してあります.
とは3本の物差しを用意するだけでなく,おのおのの点で物差しをどの角度に当てるかもすでに指定してあります.
メッシュを構成した時に物差しと分度器は含まれています.(計量がはいっています.)
ちなみに3本の物差しは同じである必要はありません.(場所によって伸び縮みしても良いです.)
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/18(Thu) 00:44)
MXKさん
> note (1)の |d4dc77d4d7daf5b9464b7e0ed6d91e93| は座標のメッシュがつくる管の性質ですね. > |7295de3befe24d5b71cac6249ba6abbc| を引き継いでいるのですね.
そうです.メッシュを構成するふたつの曲面 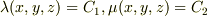 の交線は
の交線は 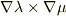 に平行です.この交線を束にしたものが束ベクトルあるいは管ベクトルであり,座標系の定義により交線には始点終点はない(管が消滅しない)のでdivergence freeになります.
に平行です.この交線を束にしたものが束ベクトルあるいは管ベクトルであり,座標系の定義により交線には始点終点はない(管が消滅しない)のでdivergence freeになります.
って,釈迦に説法....
Re: 初めまして
zoro さんのレス (2007/01/18(Thu) 02:30)
toorisugari no Hiroさんの「2007/01/18(Thu) 00:19 No.13762」 についてコメントします.
重心,正確に言えば質量中心のヴェクタは物理的実在だと解釈します.たとえ,その導出過程に運動量とか速度が使われたからと言っても,質量中心のヴェクタ自身に物理的意味が無いというのは変ですね.
例えば,宇宙に孤立した物体の質量分布が既知ならば「その物体に1つだけの外力を加えて加速するも,回転を生じないように力を加えるためには重心に向かって力を加えること」は高校生でもご存知でしょう.
先ほどご紹介した秋田工業高等専門学校の「Yamamoto's Laboratory」サイトの接ヴェクタの導出は読ませて戴きました.デカルト座標から出発して,他の直交座標系に導く説明は具体的で,よく判りました.
#このサイトは明快に説明して在るので,高校生でも微分の素養があれば,途中までは理解できるような気がします.
結局,たの直交座標系との幾何学的接点は,位置ベクトルの全微分において,ある一つの座標の変化だけを許して,他の2つの座標を一定に保持した時に出来る微分ヴェクタをもってその接ベクタと考えると言う点に帰着し,その規格化のために計量因子が出ることが判りましたし,遂に,自分でも計算しました(笑).
#この位置ヴェクタの微分をもう少し纏めて分析すると,幾つもの解釈が出そうですね. #数学の強い方々は,直ぐに抽象的な幾何学的把握が出来るのでしょうが,多くの物理の学生はそれが出来ないのだろうと思います.(自己弁護) #でも,数学のセンスのない物理の学生に対する講義ノートが欲しいなぁ,ですよ.
とすると,少なくとも,直交座標系(変数のセット;円筒座標系:r,φ,z)に限定する限り位置ヴェクタの微分ヴェクタの関数関係自身から基底を作り出せる,言い換えれば,直交座標系を決めれば基底もきまると言うことと考えることが出来ました.
一度,座標系と基底が決まれば,位置ヴェクタは,質量中心のヴェクタも含めて,それらの物理的実在を否定する論拠は見当たらないと感じます.これらに付いては,もう少し勉強してから判らなければ別途質問します.
当面は,上記サイトに紹介のあった
ジョージ・アルフケン. ベクトル・テンソルと行列. 基礎物理学 1. 講談社, 1993.
を拝見して,勉強したいとおもいます.
とても示唆的なご解説有難うございました.今回の割り込み質問はこれで終了させていただきます.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/18(Thu) 02:47)
重心ベクトルについては以前の記事を修正しました(簡潔にしました).
位置ベクトルは正確にはベクトルではない(完全に否定しているわけではありませんよ.)の議論については「ベクトル空間」と「アファイン空間」(アフィン空間)というキーワードで調べられると良いです. 文献としてアーノルド「古典力学の数学的方法」岩波書店(絶版)を図書館などで見つけられたら読まれることをおすすめします.
Re: 初めまして
zoro さんのレス (2007/01/18(Thu) 11:13)
toorisugari no Hiroさん,
> 重心ベクトルについては以前の記事を修正しました(簡潔にしました).
ご配慮有難うございます.位置ヴェクタは,原点が固定された座標という意味で特殊なヴェクタだという単純な観点に立っていました.しかしこの重心の計算操作を考えると位置ベクトルの質量重み付き総和では限定的に,原点をずらしていますね.しかし和をとったヴェクタの原点は,何時も座標原点です.これは電場とか力を現すヴェクタの加法とすこし違うと思います.
#なお,位置ヴェクタに限らず,力のヴェクタだって,気楽に原点を変えるとモーメントがおかしくなりますね. #それこそ,物理に出てくるヴェクタの数学的本性の本格的だが物理屋の視点に乗っ取った解説が望まれるところです.
他方,ユークリッド空間に於けるデカルト座標表示の位置ヴェクタの全微分 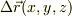 から出発して,他の直交座標系,例えば
から出発して,他の直交座標系,例えば 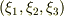 に変換する時に,2座標値を固定して,残りの1座標の変化を考えてその接ヴェクタ,敢えて明言すればその方向の基底を決めることが出来る.まさにこの能力こそが「位置ヴェクタのみが幾何学的要因を内在している」と思えます.
に変換する時に,2座標値を固定して,残りの1座標の変化を考えてその接ヴェクタ,敢えて明言すればその方向の基底を決めることが出来る.まさにこの能力こそが「位置ヴェクタのみが幾何学的要因を内在している」と思えます.
それ故に,デカルト座標以外の角度を成分に持つ座標では,その基底は必然的に局所的に成ります.従って,粒子運動の軌道を表現する時には必然的に,その粒子の居る位置での局所的基底となり,あたかも粒子に座標が張り付くのだろうと思います.
話を戻しますと,基底をだす計算過程は,二つの座標を一定にたもった場合の等座標値面の計算と見ることも出来ると思います.これに付いては重力場,電場などで散々計算をしている等ポテンシャル面と似た解析が可能なわけですね.逆に,これらの知識を座標に戻して考えると見通しが良くなるよ,というのが「No.13751」でお示しになった事だろうと推察できるようになりました.ついては,ご紹介の ・アーノルド「古典力学の数学的方法」岩波書店(絶版) を拝見してみようと思います.
最後になりますが,自分は,基底が物理的な長さの尺度と無関係なものであるのにも関わらす,数的単位,無次元というべきか,を持つことが不安でした.が,No.13756でご紹介した秋田工業高等専門学校の「Yamamoto's Laboratory」サイトの接ヴェクタのお話から,基底は明白に「無次元」であり,その基底セットを他の各種物理量のヴェクタが共有するのだと思えるようになりました.
このように物理的ヴェクタがその物理量に対応する次元をもち,基底は無次元であることを明記されていたのは,自分の知る限り 「数理科学SGCライブラリ-39 マクスウェル方程式」北野 正雄・著,サイエンス社,2005. だけです.しかし,この本のp10の「2.2.3 物理次元とベクトル」の項にヴェクタの内積に絡めた説明がありますが,基底の解説が不明確なままにされているので,逆に混乱を招いていると感じます.
ということで,長年に渡る疑問が解けそうなので,当面,ご紹介の本を中心に勉強したいと思います.では,失礼します.
Re: 初めまして
MXK さんのレス (2007/01/18(Thu) 11:31)
位置ベクトルは適用範囲が限定されていますね.曲線座標を使う場合やや苦しくなり,空間そのものが曲がっている場合には全くだめになりますね.(平坦な高次の空間に埋め込まれているとすれば,使えなくはありませんが.) 球面上の図形の重心(たとえば日本の重心)などを考えると,単純な式ではダメなことが理解しやすいかも知れません.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/18(Thu) 18:05)
> なお,位置ヴェクタに限らず,力のヴェクタだって,気楽に原点を変えるとモーメントがおかしくなりますね.
作用点と原点は違う概念です.「束縛ベクトルか自由ベクトルか」と「点かベクトルか」は別問題です.
位置ベクトルは純粋なベクトルではない(アフィン空間の元である)という問題,基底は位置に付随しているのか粒子に付随しているのかという議論については,もう,控えます.
ただ,先に示したアーノルドの本に好きな言葉があるので,それを「編集して」のせます.まず,解説
「(1)アフィン空間 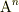 は座標系の原点が固定されていないことだけが
は座標系の原点が固定されていないことだけが  次元実線形空間
次元実線形空間 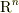 と異なる.
(中略)
(2)世界は4次元アフィン空間である.(脚注)
(以下略)
」
とあり,脚注を読むと
と異なる.
(中略)
(2)世界は4次元アフィン空間である.(脚注)
(以下略)
」
とあり,脚注を読むと
「脚注:昔は,世界はアフィン構造でなく,線形空間の構造(天動説+天地創造)をもつと考えられていた.」
と書いてありました.アーノルドのユーモアのセンス,好きです.
自然基底については"Geometrical Vectors"がおすすめです.先にdivの一般座標系での導出をしましたが,あれをほとんど式や公式を使わず絵だけで完璧に説明しています.ここでも何回か紹介してるので検索をかけてください.
> 基底は無次元であることを明記されていたのは
正規直交基底なら,無次元です.でも,一般の自然基底は無次元ではありません.
確かに,単位ベクトルの次元の問題,有次元のベクトル量をどう図示するか,それと単位ベクトルの関係の問題は,実は,結構難しい問題ですよね.
Re: 初めまして
zoro さんのレス (2007/01/18(Thu) 20:10)
>アーノルドの本に好きな言葉があるので,それを「編集して」のせます.
この本は面白そうなので,図書館にいって手配してきました.都の図書館からの借用なので来週になります.座標変換は短そうなので,フル・コピーして勉強させていただきます.
>自然基底については"Geometrical Vectors"がおすすめです.
昨年, toorisugari no Hiroさんのご紹介があった時に入手したのですが....基底の論議がないままに話が進行するのに耐え切れなくて放棄しました.しかし,再度のお勧めに従って,最近得意になってきた「パラパラめくり法」で拝見したところ,第6章の"Coordinates and Components"を眺めていると,今回のご論議に近そうな部分が散見されました.
そこで,気をよくして初めに戻ると,基底に寄らないヴェクタの説明,恐らくtoorisugari no Hiroさんが今回も何度もご主張されている感じがこれかな?,と思えるようになりました.
アーノルドさんの本が借用できるまで,§6→§1→§2→...,といった読書をトライしたいと思います.こんな面白い経験ができて,とても感謝です.
追伸: >作用点と原点は違う概念です.「束縛ベクトルか自由ベクトルか」と「点かベクトルか」は別問題です.
私は,物理の問題の中で,このような観点での疑問に遭遇していません.今後の勉強で問題意識が発生した時に,ご相談したいと思います.
Re: 初めまして
toorisugari no Hiro さんのレス (2007/01/22(Mon) 16:10)
> このように物理的ヴェクタがその物理量に対応する次元をもち,基底は無次元であることを明記されていたのは,自分の知る限り 「数理科学SGCライブラリ-39 マクスウェル方程式」北野 正雄・著,サイエンス社,2005. だけです.
この本を読んでみました.非常に良い本ですね.感動しました.
ベクトル空間で物理的次元を考えている本は初めてでしたし,ほかにも,「初等的」故に他の本では触れていない(本当は初等的でない基本的な)事まで,書いてあって驚きでした. (例えば,内積(メトリック)とスカラー積(ドット積)を区別していたり,電場をどういう風に観測するかという考察から,テンソルを決定したりとか....) 肝心の電磁気学の方はさほどの切れ味を感じませんでしたが(今までの教科書を覆すというより上級者向けのTipsという感じ),ベクトルの初歩についてこれだけの内容を書いた和書は初めてでした.ベクトルの初歩,ベクトル・テンソル解析,δ関数,電磁気学の教科書の一つのreferenceになる良書です.
良い本を教えてくださり,ありがとうございます. (りんごさんが,最初にこのサイトに紹介されたのですね.改めてお礼を言います.)
粘性流体とベクトル解析と電磁気学と
zoro さんのレス (2007/01/22(Mon) 19:48)
タイトルを明示的にして見ました(笑).
toorisugari no Hiroさん,
"Geometrical Vectors"と言い,これらの本は「新規性の高い解釈」を問う本であり,教科書のレベルに到達しているものとは思えません.むしろ,我々が,彼等の言わんとしている本質を咀嚼して,若い世代に解説できると素晴らしいと思います.
#長くて,遠い道のりだと思いますが,一歩を踏み出すしかない.
>肝心の電磁気学の方はさほどの切れ味を感じませんでしたが,ベクトルの初歩についてこれだけの内容を書いた和書は初めてでした.
また偶然に見た本ですが,
「新しい計算電磁気学 [基礎と数理]」 五十嵐一/亀有昭久/加川幸雄/西口磯春/A.ボサビ[共著] 培風館,2003-12, ISBN:4-563-06731-8.
目的論的性格が強い本ですが,「その計算手法を開拓する為に,理論的枠組みにすら立ち入って考察した」という意味では,「物理の電磁気学」に接する者として刺激てきな本であり,敬意を表します.
こう考えてみると,流体力学・電磁気学といった古典的場の理論体系を「エレガントでしかも見通しの善い新たな統一的な器(解析表現)」に入れてみたいものですね.
Re: 粘性流体とベクトル解析と電磁気学と
toorisugari no Hiro さんのレス (2007/01/22(Mon) 20:16)
> タイトルを明示的にして見ました
ありがとうございます.気になってはいたんですが,タイミングが...
> むしろ,我々が,彼等の言わんとしている本質を咀嚼して,若い世代に解説できると素晴らしいと思います. > #長くて,遠い道のりだと思いますが,一歩を踏み出すしかない.
ま,我らにどれだけの力があるか問題ですが,少なくとも,「良い本は購入する」「良い本は紹介する」という,誰でもできる,そして一番大事な貢献をすることが大事ですよね.
> 「新しい計算電磁気学 [基礎と数理]」
おお.これも読んでみますね.
> こう考えてみると,流体力学・電磁気学といった古典的場の理論体系を「エレガントでしかも見通しの善い新たな統一的な器(解析表現)」に入れてみたいものですね.
完全にエレガントな形式にしたものは「多様体」と言う形に完成してますね. ただ,物理の匂いがしない.....
物理の匂いがする(直感的な理解から導いた)「エレガントでしかも見通しの善い新たな統一的な器(解析表現)」,あるいは多様体論の物理的表現,ができないかなと思っています.
そのためには,電磁気学と流体力学(と相対論)をもっと勉強しなければ...(sigh)
Re: 粘性流体とベクトル解析と電磁気学と
zoro さんのレス (2007/01/22(Mon) 22:12)
toorisugari no Hiroさん,
>完全にエレガントな形式にしたものは「多様体」と言う形に完成してますね. >ただ,物理の匂いがしない..... > >物理の匂いがする(直感的な理解から導いた)「エレガントでしかも見通しの善い新たな統一的な器(解析表現)」, >あるいは多様体論の物理的表現,ができないかなと思っています. > >そのためには,電磁気学と流体力学(と相対論)をもっと勉強しなければ...(sigh)
なるほど,言い得て妙とは,この事だと思いました.私も,このスレッドでの質問,渦度場の計算の下調べをする為に,所謂ベクトル解析の解説サイトを拝見していると,数学的には正しそうでも,実際に手計算する時に見やすく使える公式がなかったり,単位直交ヴェクタの図示がなかったりという実際的な問題点から始まって微分演算子,積分公式などの解説を拝見していると,数学と物理にはかくも大きなギャップがあるのを再認識させられています.
『オイラー〜マクスウェル〜アインシュタインを結ぶ「物理の匂いがする多様体論的解析法」』を目指してチョコチョコとトライしましょう.ドン・キ・ホーテズかもしれませんが(笑).
Re: 粘性流体とベクトル解析と電磁気学と
zoro さんのレス (2007/01/23(Tue) 14:52)
>完全にエレガントな形式にしたものは「多様体」と言う形に完成してますね.
私は先ず,古典物理学の場を考える時に,物理的空間と数学的空間との分離識別を明快にすることが大切だと思います.
まだ朦朧としていますが,「計測できる物理的空間」には,その背景に「実数だけで記述される数学的空間」が必要で,この両者のもつ意味が明確になると宜しそうだと感じます.
物理屋教育では,上記の明瞭なイメージを基に,「計測できる物理的空間」に専念すればよいのではなかろうかと,想像しています.