静電ポテンシャルについて
静電ポテンシャルについて
けん(大学1年) さんの書込 (2007/01/10(Wed) 19:06)
電磁気学の質問です.
E=(2xz,2yz,x^2+y^2-2z^2)
dr=(dx,dy,dz)
φ=-∫(原点からr=(x,y,z)まで)E・dr =-((x^2)z+(y^2)z+((x^2)z+(y^2)z-(2/3)z^3))
としたのですが,答えが φ=-((x^2)z+(y^2)z-(2/3)z^3)
となっています.勾配ををとると確かに自分の出したものは間違いだと分かるのですが, φ=∫(原点からr=(x,y,z)まで)E・dr としてはいけないのですか?
Re: 静電ポテンシャルについて
サボテン さんのレス (2007/01/10(Wed) 20:30)
φ=∫(無限遠からr=(x,y,z)まで)E・drで合っています(−符号がついたか どうかが分かりませんが.記憶が曖昧で・・・すみません)
間違っているのは積分過程です.
Re: 静電ポテンシャルについて
りんご さんのレス (2007/01/10(Wed) 20:31)
すこし話がそれますが,私も,何かのときに積分の初期値をどうとれば良いか忘れる事が在ります.
また,積分の初期値は,原理的には,無限遠方である要請はどこにもありません.ただ多くの場合,遠方で電場が消失する事が多いので無限点を初期値に取ります.でも原子の電場のように,原子核の電場が電子の電荷分布によって遮蔽されるようなばあい,適当な半径より電場が消失するとして考えることもできますね.
で,本論に戻ります.私の場合,次のような感じで思い出します;
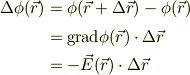
そこで,自分の好きな点, 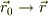 までの経路積分を考えれば,
までの経路積分を考えれば,
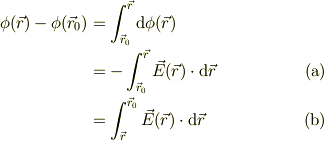
式(a)は普通の定義ですが,式(b)は電極間の電位差を求める時,出発点の電位から始まって到着点までの経路積分をだすとすれば,考える時に間違えにくくなります.
私は,ほとんどの場合,ポテンシャルの中心から,ジェット・コースタで落下しながら積分する感じが好きなので,自分的にはほとんど式 (b) で計算しますが,人に説明する時には式(a)に戻して置きます.
他方,解ですが,積分をもう一度冷静に見直す事をお勧めします.
Re: 静電ポテンシャルについて
ミュフ猫 さんのレス (2007/01/10(Wed) 21:12)
けん(大学1年)さんへ
スカラー場φの解が存在するならば,ベクトル場Eは保存場ですから, 積分経路は自由に選べます. この場合,原点を基準にした方がいい様に思います. なぜならば,原点における電場は明らかに0だからです. 無限遠を基準にするのはまずいと思います. なぜならば,方向によって電位が異なってくると思われるからです. 問題を見てませんから,良くわかりませんが, 解答を見る限り,原点が基準になっているようです. なお,積分計算においては,具体的にどういう経路で計算するのか, 明確にした上で,行うことが重要に思います. そうすれば,定数の扱いを間違わずに済むと思います.
呼び捨てになってました.ご容赦ください.m(_ _)m あせった.(^_^;)
Re: 静電ポテンシャルについて
yama さんのレス (2007/01/10(Wed) 22:23)
電場の成分の値が無限遠で発散するので無限遠を基準にはできないでしょう. それより問題なのは電場の回転が0でないことで,これではポテンシャルが定まりません.
Re: 静電ポテンシャルについて
ミュフ猫 さんのレス (2007/01/10(Wed) 22:31)
yamaさんへ
×E=(2xz,yz,x^2+y^2-2z^2)→○E=(2xz,2yz,x^2+y^2-2z^2) × φ=-(x^2)z+(y^2)z-(2/3)z^3→○φ=-(x^2)z-(y^2)z+(2/3)z^3
ということじゃないのでしょうか.w
Re: 静電ポテンシャルについて
りんご さんのレス (2007/01/10(Wed) 22:42)
なるほど, 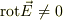 なんてあり?そういえば,一部に対称性が欠けているような.
なんてあり?そういえば,一部に対称性が欠けているような.
しかし,回答者に設問の誤りを指摘させるような問題はアンフェアだと思います.この問いが公の資料ならば,訂正を要請する必要がありますね.
ただ,試験を受ける身としては,設問がおかしそうならば; ・回転を計算して,それを示しながら, ・「保存場でないようです」がどうしましょう? と質問すれば,テストは合格するでしょうね.
Re: 静電ポテンシャルについて
けん(大学1年) さんのレス (2007/01/18(Thu) 16:49)
レスありがとうございます.電場の式が間違っていました.申し訳ありません.
原点を基準にして積分してみたのですが,
E=(2xz,2yz,x^2+y^2-2z^2)
dr=(dx,dy,dz)
φ=-∫(原点からr=(x,y,z)まで)E・dr =-∫(原点からr=(x,y,z)まで)(2xz,2yz,x^2+y^2-2z^2)・(dx,dy,dz) ここで, ∫2xzdx=(x^2)z ∫2yzdy=(y^2)z ∫(x^2+y^2-2z^2)dz=(x^2)z+(y^2)z-(2/3)z^3 であることより, φ=-((x^2)z+(y^2)z+((x^2)z+(y^2)z-(2/3)z^3)) という計算をしました.この積分が間違っているのでしょうか?
Re: 静電ポテンシャルについて
ミュフ猫 さんのレス (2007/01/18(Thu) 19:33)
けんさんへ
ベクトルの線積分なので,具体的に経路を決めることが必要に思います. 例えば, (0,0,0)→(x,0,0)→(x,y,0)→(x,y,z) と,このように選んだ場合,けんさんの計算方法が間違いであることに 気づくと思います.
Re: 静電ポテンシャルについて
けん(大学1年) さんのレス (2007/01/20(Sat) 18:39)
経路を具体的に決めると正しい答えを出せるのですが,上記の自分の計算法のどこがおかしいのか分からないのです.
Re: 静電ポテンシャルについて
クロメル さんのレス (2007/01/20(Sat) 21:10)
∫2xzdx=(x^2)zは,zが変化しないように積分をしているので, x成分については,(0,0,0)→(x,0,0)までの経路で積分して,y成分については,(0,0,0)→(0,y,0)まで積分している.そういうめちゃくちゃなことをしているっていうのはわかりますか?
Re: 静電ポテンシャルについて
りんご さんのレス (2007/01/20(Sat) 22:44)
やや混乱されていると思うので,他の経路で説明してみます.
経路を原点(0,0,0)からz軸に沿って(0,0,z)まで積分することだけを考えます.
この積分は丁寧に書くと;
![\int_{(x'=0,y'=0,z'=0)}^{(x'=0,y'=0,z'=z)}\vec E(\vec r')\mathrm{d} \vec r' &=\int_{z'=0}^{z'=z}\left[ E_{z}(x',y',z')\right]_{(x'=0,y'=0)}\mathrm{d} z' \\&= \int_{z'=0}^{z'=z}\left[ x'^{2}+y'^2-2z'^{2}\right]_{(x'=0,y'=0)}\mathrm{d} z' \\&= \int_{0}^{z}(-2z'^{2})\mathrm{d} z'](http://hooktail.maxwell.jp/bbslog/9657f82f7b6efb7e626c4386d0ba12fd.png)
ですよね.
面倒でも,積分中のパラメータを陽に書き出してみれば,計算ミスの元凶が見つけ易くなるでしょう.
Re: 静電ポテンシャルについて
けん(大学1年) さんのレス (2007/01/30(Tue) 17:46)
レスありがとうございます.計算ミスの原因は分かりました.ありがとうございます. 経路を指定せずに一般的に求めることはできるんですか?
Re: 静電ポテンシャルについて
りんご さんのレス (2007/01/30(Tue) 18:35)
No.13637やNo.13639をよく見て勉強してください.
これらのコメントに共通するのは,保存場の線積分を任意の連続回路を一周するとゼロになる性質,ストークスの公式に基づきます.
これが利用できれば
>経路を指定せずに一般的に求めることはできるんですか?
といった手の掛かる計算をするより,場面に応じて使いやすい座標系で,簡単な経路をとる方が間違いが少なく,検算も楽ですよね.
我々は,数学の問題を解いているのではなく,物理現象を記述する為の方程式系を解析して,その物理的な意味を理解しようとしている事が大切だろうと思います.
Re: 静電ポテンシャルについて
けん(大学1年) さんのレス (2007/01/30(Tue) 23:31)
それもそうですね.
でも,ストークスの定理が成り立っていることをこの例において確かめたかったので経路を指定せずに一般的に求めようとしたんですが,それは大変ですか?
Re: 静電ポテンシャルについて
ミュフ猫 さんのレス (2007/01/30(Tue) 23:39)
けんさんへ
>ストークスの定理が成り立っていることをこの例において確かめたかった >ので経路を指定せずに一般的に求めようとしたんですが,それは大変ですか?
それなら, rot(E↑(x,y,z))=0 を計算で証明すればいいと思います. これは,電場が保存場のときに成り立つ方程式です.
Re: 静電ポテンシャルについて
けん(大学1年) さんのレス (2007/01/30(Tue) 23:49)
回転が0であることからの証明もあるんですね.忘れていました.すみません.
でも,どうしても経路を指定せずに一般的に求めたいのですが,そのような計算方法はあるのですか?
Re: 静電ポテンシャルについて
りんご さんのレス (2007/01/31(Wed) 00:04)
>でも,ストークスの定理が成り立っていることをこの例において確かめたかったので経路を指定せずに一般的に求めようとしたんですが,それは大変ですか?
これはこれで面白いと思います.偏微分方程式の特性曲線を出すような要領で,2点間を連絡する曲線をパラメータ 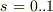 により,適当な初等関数(自分で積分しやすく,1価関数なら何でも良いはずですね)をつかって
により,適当な初等関数(自分で積分しやすく,1価関数なら何でも良いはずですね)をつかって
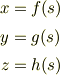
で与えれば,sについての積分で求められませんか?
確かに,一つの法則を色々な手法で計算する事は,イメージを確実にする為に大事だと思います.私も1年生の秋頃,球殻状に分布した電荷,ないしは質量が「その球殻内部に場を作らない」ことを証明する計算で,四苦八苦したことが在ります(笑).なんども計算をやり直しているうちにノート一冊と,数学事典を購入するはめになったと思います.
是非ともトライすると一生の記念になることを請け合います.
Re: 静電ポテンシャルについて
けん(大学1年) さんのレス (2007/01/31(Wed) 00:35)
偏微分方程式の特性曲線というのが何か分からないので,それを習ってからやろうと思います.どうもありがとうございました.
Re: 静電ポテンシャルについて
toorisugari no Hiro さんのレス (2007/01/31(Wed) 00:40)
> どうしても経路を指定せずに一般的に求めたいのですが,そのような計算方法はあるのですか?
このような感じでしょうか?
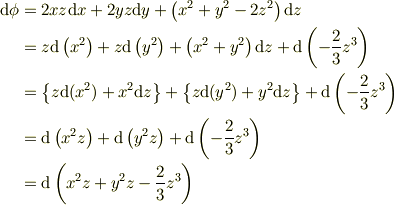
あえてやるほどきれいな解き方ではないですね.
Re: 静電ポテンシャルについて
けん(大学1年) さんのレス (2007/01/31(Wed) 00:45)
ありがとうございます.今度からは経路を指定して計算することにします.
Re: 静電ポテンシャルについて
りんご さんのレス (2007/01/31(Wed) 11:58)
ちょっと余計なお世話かもしれませんが.
No.14016の方法は,最終的には3つの積分を一挙に足し合わせるものです.
その意味では,No.14019は,直交している系では,注意深く計算して,全微分に持ち込めれば良いという意味で,スマートな解だとおもいます.なぜ,この方法が正しいのかを味わったら,この方法も自分の道具箱に入れるといいと思います.
けんさんの疑問の立て方は,とても素晴らしいです.この調子で,どんどん進んでください.しかし,回答者へは,今少し早い応答があると良いですね.恐らく,多くの方が心配してご覧になっていたように思います.
「若いときに習得した知恵は一生もの」の様です,おおいに研鑽に励んでくたさいね.
Re: 静電ポテンシャルについて
toorisugari no Hiro さんのレス (2007/01/31(Wed) 14:24)
もっとスタンダードな方法を述べ忘れてましたね. 本質的には全微分を求める方法と同じですが,機械的にできます.
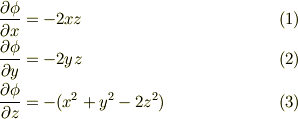
を(偏微分であることを考慮して)不定積分すればいいのです. (1)より
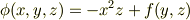
(  :未定の関数)
これを(2)に代入して
:未定の関数)
これを(2)に代入して
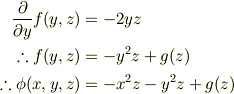
(  :未定の関数)
これを(3)に代入して
:未定の関数)
これを(3)に代入して
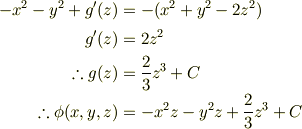
( 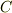 :未定の定数)
通常の,経路を指定した線積分と違い,この方法では
:未定の定数)
通常の,経路を指定した線積分と違い,この方法では 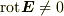 のとき,最後の常微分方程式が解けない形(ex.
のとき,最後の常微分方程式が解けない形(ex. 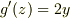 :
:  は独立変数)になるので,解は出ません.
は独立変数)になるので,解は出ません.
Re: 静電ポテンシャルについて
けん(大学1年) さんのレス (2007/01/31(Wed) 19:01)
りんごさん,ありがとうございます.疑問はよく出てくるんですが,あまり自分で解決できません.考えても分からなかったり,調べても分からないのです.将来は研究者になりたいのですが,今のように,自分で解決できない状態だと,研究者には向いてないでしょうか?
toorisugari no Hiroさん,ありがとうございます.理解が深まりました.
Re: 静電ポテンシャルについて
りんご さんのレス (2007/01/31(Wed) 20:23)
>疑問はよく出てくるんですが,あまり自分で解決できません.考えても分からなかったり,調べても分からないのです.
私は,教育者でないので本当の所は判りません.でも,物理を勉強する上では「疑問を持てる」事はとても大事だとおもいます.頭が良すぎて「右から左に理解できる人」は数学とか,別の分野が向いているかも知れませんね.
他方,「疑問の処置」ですが,色々な方法が在ると思いますが,お勧めは;
(1)とにかくノートにとる.媒体は何でもよし.見返る準備だけはする(何十年後にしか見ないかも知れませんが).
ただノートといえども,「起承転結」は付けましょう.図も簡単で良いから書きましょう.「アスキー・アート」程度でも結構,表現力が在るようです.面倒ならノートの半分側に絵を付ける訓練をすると良いかも.
年を取るにつれて,物理の底力は,「作文」と「絵」ではないかと思っています.と書いた手前,例題を作って見ました(笑);
<pre>《物理の世界に欠かせない材料》
・専門的学力「怖がらずに前進できる意志力」「多角的思考」
・基礎的学力「(物理)数学」「物理」「英語による自己表現」
・物理的洞察力「疑問を持てる心」←自我の内側自我の外側→「対話」
・基本能力「作文」ーーーーー「絵」
・人間力「好きな趣味」「体力:水泳はお勧め」 </pre>
(2)解決は無理に急がない.これからの講義や,本などの勉強で,思いがけずに解けるようになるかもしれない.自分で見つけた疑問を,じっくり煮詰めながら解決を探る練習は,一種の知的ゲームと思えば楽しいですね.
(3)(2)と矛盾するようですが,ものすごく疑問が煮詰まって苦しくなるときは,自分であまり悩まないのも一方だと思います.友人とか,掲示板とか,第三者に自分のアイデア(疑問もアイデアだと思います)を示して,それに対する他人の応答を理解・観察するのは,通常の講義で得られない「何か」が在ると感じます.
>将来は研究者になりたいのですが,今のように,自分で解決できない状態だと,研究者には向いてないでしょうか?
こんな事が気楽に判定が付くなら,大学なんて無用になりますね.ある個人について,いくら詳細に検討してもその能力を決める事は出来ないと思います.
時代背景とか思考形態とのマッチング,運・不運などもありますし.自分の生涯ですから,自分でリスクをしょって冒険するも,しないも,その人の決断によると思います.
あるとき,恩師のお一人が,「運命の神様には前髪しかない.良い前髪が来たら掴み取る用意をしておきなさい」と言われました.
大学1年生は,まさに準備中の日々ですよね.
Re: 静電ポテンシャルについて
けん(大学1年) さんのレス (2007/02/02(Fri) 12:35)
りんごさん,ありがとうございます.すごく参考になります.印刷までしてしまいました(笑) これからは,疑問をノートにとることをしてみようと思います.