k さんの書込 (2007/01/09(Tue) 20:19)

大学でレポート課題が出たのですが，わからないので質問させてください．． 静止している調和振動子(固有振動数をω0とする)に，ある時刻からF0sinωtで表せる外力が作用し始めたとき，振動子の運動を(1)初期，(2)十分時間が経ってからについて求めよ．特に，(1)の場合について，ωがω0に近づいた場合の解の様子を求めよ．

という問題なのですが，(1)と(2)の違いがよくわかりません．どなたか知恵を貸していただけないでしょうか．．

CO さんのレス (2007/01/09(Tue) 21:12)

こんばんは．

とりあえず運動方程式を書き下し，解いてみてはどうでしょう． その解が 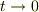と 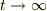の極限でそれぞれどう振る舞うかを見れば良いと思います．

そして 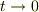の漸近解が 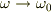でどういった振る舞いをするのかを見ると良いのではないでしょうか．

k さんのレス (2007/01/12(Fri) 05:32)

返信が遅くなって申し訳ありません．微分方程式を解くのにかなり時間がかかってしまって…．． x(t)=…という形で一応答えを出したのですが，t→0,t→∞でどう振舞うのかがいまいちわかりません．（x(t)を書きたいのですがLaTeXの表示がどうもうまくいかなくて…すいません．）

CO さんのレス (2007/01/12(Fri) 08:12)

> x(t)を書きたいのですがLaTeXの表示がどうもうまくいかなくて…

latex の扱いに慣れていないようであれば，普通にテキストで書いてくださっても構いません． 解を示してみてください． :)