2体問題について
2体問題について
ゆう さんの書込 (2007/01/08(Mon) 02:11)
こんばんは,大学一年生のゆうといいます. 長文なのですが,2体問題について教えてください. 問1〜6まで解いてみました.この答えで合っているのか自信がなくて・・・チェックをお願いできないでしょうか? また,この問題は物体1,2では同じ質量になっています.これが違う場合などでも問3は同様に解けるのでしょうか? よろしくお願いいたします.
【問題】
自然長 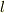 ,バネ定数
,バネ定数  の軽いバネの両端に質量
の軽いバネの両端に質量  の二つの小さな物体1と2をつなぎ,バネを自然長より
の二つの小さな物体1と2をつなぎ,バネを自然長より  だけ伸ばして水平な台の上に置いた.
時刻
だけ伸ばして水平な台の上に置いた.
時刻  で静かに手を話すと二つの物体は振動を始めた.手から離した後の運動について考える.
で静かに手を話すと二つの物体は振動を始めた.手から離した後の運動について考える.
 軸をバネの伸び方向にとり,時刻
軸をバネの伸び方向にとり,時刻  で物体1と2の位置は
で物体1と2の位置は 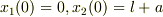 とする.
とする.
-------------------->  |−−○〜〜〜〜〜○
------
|−−○〜〜〜〜〜○
------ 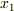 ------
------ 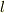 --
-- 
問1.2つの物体の位置が 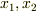 のとき,物体1に働く力
のとき,物体1に働く力 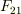 と物体2に働く力
と物体2に働く力 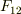 を答えよ.
解
を答えよ.
解
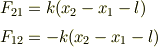
それぞれを式(1),(2)とする.
問2.物体1と2の運動方程式を求めよ. 解 式(1),(2)より
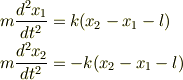
それぞれを式(3),(4)とする.
問3.質量中心 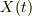 の運動方程式を求めよ.
解
の運動方程式を求めよ.
解
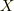 は質量中心なので,合計の質量を
は質量中心なので,合計の質量を 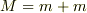 とする.
とする.
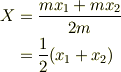
これを式(5)とする.
式(5)で運動方程式の左辺を立ててみると
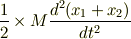
となり,質量中心 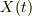 の運動方程式は
の運動方程式は 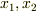 を足して
を足して 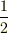 すればよい.
つまり
すればよい.
つまり
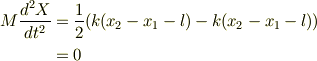
となる.これを式(6)とする.
問4.質量中心の位置を時間の関数として求めよ. 解 式(6)を2回積分する.
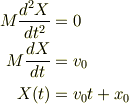
となり,題意より  の場合
の場合 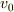 は0,
は0, 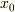 は
は 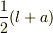 となる.
よって
となる.
よって
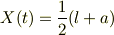
となる.これを式(7)とする.
問5.相対座標 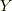 (物体1から2)の運動方程式を求めよ.
解
相対座標は
(物体1から2)の運動方程式を求めよ.
解
相対座標は  したものなので式(4)-式(3)をしたものである.
したものなので式(4)-式(3)をしたものである.
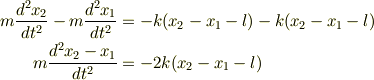
ここで 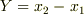 とすると.
とすると.
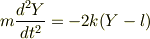
となる.これを式(8)とする.
問6.相対座標を時間の関数として求めよ.
解
式(8)へ 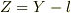 ,
, 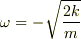 とし代入した.
とし代入した.
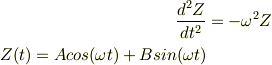
となる.これを式(9)とする.
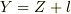 を式(9)へ代入
を式(9)へ代入
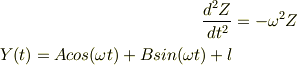
AとBを求める,  の場合,
の場合, 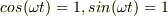 ,
,  なので
なので
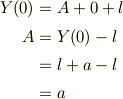
となる.
Bは 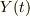 を一度微分し初速度から求める.
を一度微分し初速度から求める.
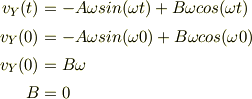
となり, 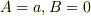 となる.
となる.
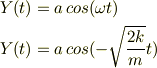
Re: 2体問題について
yama さんのレス (2007/01/08(Mon) 10:34)
Y=Z+l なので +l が必要です.また cos の引数についている - は除くことができます.というよりも初めから 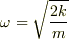 としたほうがよかったでしょう.結局
としたほうがよかったでしょう.結局
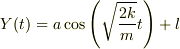 となりますね.
t=0 のとき sin(ωt)=1 となっているのは単純な書き間違いでしょうね.細かくは見ていませんが,ざっと見たところでは他に誤りはなさそうです.
となりますね.
t=0 のとき sin(ωt)=1 となっているのは単純な書き間違いでしょうね.細かくは見ていませんが,ざっと見たところでは他に誤りはなさそうです.
質量が等しくない場合も同様に解けます.一般に,このような2体問題は,相対座標と換算質量を用いることによって1体問題に帰着させて解くことができます.
Re: 2体問題について
ゆう さんのレス (2007/01/08(Mon) 13:26)
こんにちは. お返事ありがとうございます.
そうですね, 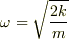 とした方が良いですね.
t=0のときsin(ωt)=0ですね.^_^;
最終的には
とした方が良いですね.
t=0のときsin(ωt)=0ですね.^_^;
最終的には
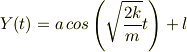
でした. ありがとうございます.
また,追加の質問なのですが,問5で物体1,2の質量が 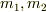 の場合
の場合
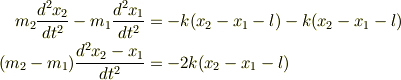
となるのでしょうか?
PS. このTeXでは数式に番号を付けられないのでしょうか? TeXの中で以下のように記入してもエラーになるようです. begin{eqnarray} Y(t) &= a , cosleft(sqrt{frac{2k}{m}} tright) + l end{eqnarray
Re: 2体問題について
yama さんのレス (2007/01/08(Mon) 14:35)
計算が間違っているようです.
2つの物体の質量が異なる場合は
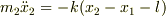 に
に 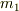 を掛けたものから
を掛けたものから
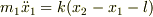 に
に 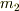 を掛けたものを差し引きます.
を掛けたものを差し引きます.
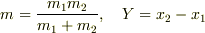 と置くことによって次の運動方程式が得られます.
と置くことによって次の運動方程式が得られます.
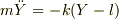
Re: 2体問題について
ゆう さんのレス (2007/01/11(Thu) 01:31)
こんばんは.
yamaさん,COさんご回答ありがとうございます. 休みの日にゆっくり見させて頂きます.
難しい問題じゃないと思うのですが,なかなか解くことができず,どこか根本的に理解不足なのかなぁと思っています. 時間をかけながらやっていきます. ありがとうございました.
