電磁気学

たむろさんの書込 (2007/01/07(Sun) 14:24)

こんにちは，はじめまして．物理はほとんど独学でやって，それでもまだ苦手で，今も大学で大変な思いをしておりますorz

早速ですが，電磁気の課題でよくわからない問題があるので，質問させてください．

(1)断面の半径がaの無限長円柱導体に電流Iが一様に流れている．透磁率をμとして，導体内部に対する単位長さあたりの自己インダクタンスを磁気エネルギーを用いて求めよ． (2)V[m^3]を占める自由空間体積の中にあるコイルを使ってB[T]の磁束密度の磁界が作られたときの磁気エネルギーを求めよ．

(1)は，自分で以下のように解いたのですが，どうもしっくりこない気がします．半径のrが残ってるのが，おかしいですよね？

アンペアの法則により導体内部の半径rの点における磁界の強さHは H=rI/2πa^2 であるので，これを単位長さあたりの磁気エネルギーWm=μH^2S/2（Sは断面積）を代入し， Wm=LI^2/2と比較して，L=μr^2/2πa^2

(2)は，問題文の「V[m^3]を占める自由空間体積の中にあるコイル…」というところで？？？となってしまっています．

ご教授いただけると幸いです．

初めまして．

(1)このような問題にであったのは初めてなので，参考程度に読んでください．

導体内部の磁場はそれであっているとおもいます．問題は導線内部の空間を通過する磁束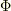， $\Phi$ をどう出すかですよね．

私は，中心に沿って，電線に仮想の断面を考えて，そこを貫く磁束密度の積分をしたら良いとおもいます．

<pre> 断面図

外径電線中心外径

|               |
|               |
|               |
|               |
|               |
|               |
|               |

r=-ar=0 r=a + -------------> ここだけ積分する．

</pre>

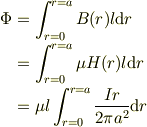
$\Phi &= \int_{r=0}^{r=a}B(r)l\mathrm{d}r\\&= \int_{r=0}^{r=a}\mu H(r)l\mathrm{d}r\\&= \mu l \int_{r=0}^{r=a} \frac{Ir}{2\pi a^2} \mathrm{d}r$

といった感じで求まりませんか？

ありがとうございます．

(1)で，なぜ鎖交磁束を求めるのか，それもよくわからないですorz すいません (2)はエネルギー密度B^2/2μに体積をかけて，求めました．

2つともなんとか回答が作れました．りんごさんどうもありがとうございました

良かったですね．

もし余裕があれば，他の方の為にも，回答をお書きになると，良い経験になるとおもいますよ．