ウィル さんの書込 (2007/01/04(Thu) 13:55)

はじめまして．数学に関して前々から疑問に思うことがあるので，質問させてただきます．

ある参考書で，

π/2<θ<πの範囲でsinθ+cosθ=(√3)/2のとき，sinθcosθの値を求めよ

という問題が載っていたのですが，次のように解答していました．

sinθ+cosθ=(√3)/2の両辺を2乗して， sin^2θ+2sinθcosθ+cos^2θ=3/4 sin^2θ+cos^2θ=1から sinθcosθ=-1/8

この解答の一行目の二乗しているところに関してなのですが，二乗してるってことは同値関係が成り立っていませんよね？だから，解答の最後に「逆にsinθcosθ=-1/8のとき…」と書かないといけないと思うのですが，どうでしょうか？お願いします．（ちなみに，数学は?Ｂまで学習しています．）

りんご さんのレス (2007/01/04(Thu) 15:27)

初めまして．

私は数学に弱いですが参考意見を書きます．

>π/2<θ<π

ですから，問題としている角度は第２象限ですから，正弦は正で，余弦は負ですから，正弦と余弦の積は負である事は間違いないですね．

>sinθ+cosθ=(√3)/2

この等式を，片々乗じても問題ありませんから，お書きになった回答は問題ないと思いますが．

もし問題が「sinθ+cosθ=-(√3)/2」だったら，どうなんでしょうね．やはり，厳格に数学的な回答を頂きたいです．識者の皆様へ．

ミュフ猫 さんのレス (2007/01/04(Thu) 15:39)

>ウィルさんはじめまして． >もう，ほとんど大学受験の掲示板と化しているようですが．ｗ >「○○のとき，××の値を求めよ．」 >「○○ならば，××の値を求めよ．」 >「○○ならば，××となることを示せ．」 >これらの表現を用いた設問は，条件命題形式のもので， >○○という基本命題が，××という基本命題の十分条件であることを意味します． >従って，この場合は，二つの命題が互いに必要十分条件であるとは限りませんし， >また，それを示す（つまり，同値関係にあることを証明する）必要もありません．

>すいません．大きな勘違いでした． >「○○のとき，××の値を求めよ．」 >「○○ならば，××の値を求めよ．」 >これらは同値関係が必要ですね．

すみません．やっぱり同値関係は必要ないように思えてきました．ｗ もう，訳がわからない．(ToT)

ｙama さんのレス (2007/01/04(Thu) 16:17)

「逆にsinθcosθ=-1/8のとき…」として推論を進めると sinθ+cosθ=(√3)/2またはsinθ+cosθ=-(√3)/2 となるので sinθ+cosθ=(√3)/2 と sinθcosθ=-1/8 は同値でないことがわかります． しかし，ミュフ猫さんが書かれているように，問題は，これらが同値であることを示すわけではないので，逆を考える必要はありません．

? π/2<θ<πの範囲でsinθ+cosθ=(√3)/2のとき，sinθcosθの値を求めよ ? π/2<θ<πの範囲でsinθ+cosθ=-(√3)/2のとき，sinθcosθの値を求めよ

このどちらの問題も，答は sinθcosθ=-1/8 でよいと思います．

りんご さんのレス (2007/01/04(Thu) 17:59)

素人意見もう一度です．

倍角の公式を考えると求める値，sinθcosθ＝sin(2θ)/2 ですね．そして，2θの範囲は，当たり前ですが， ・π<2θ<2π

と第３象限から第4象限になります．従って，この範囲の正弦の値は全て負ですね． ・-1 <= sin(2θ) <=0

他方，

ここで，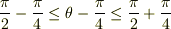

結局，題意「sinθ+cosθ=(√3)/2」によって与えられる解は，θがy軸からすこし反時計方向を向いたもので，「sinθ+cosθ=-(√3)/2」によって与えられる解は，θがy軸からすこし時計方向を向いたものでしょう．

ウィル さんのレス (2007/01/04(Thu) 22:42)

お返事ありがとうございます． 皆さんのご意見のおかげで，同値関係を意識する必要はないことがなんとなくわかりました． １つの問題を根本なところまで考えるのはもちろん必要なことだと思うのですが，追求することをやめて，「これはこうなるから，こうなんだ！」キッパリ諦めるというか納得するということも大切なのでしょう． 皆さん，ありがとうございました．