カリプソ さんの書込 (2007/01/03(Wed) 16:12)

明けましておめでとうございます．昨年はお世話になりました．ありがとうございました．そして今年も宜しくお願い致します． 早速なのですが，大学でレポートが課され，わからないので質問させてください．

xy座標上で，(a,0), (-a,0), (0,a), (0,-a)にそれぞれ-qの電荷．(0,0)に+qの電荷がある．-q電荷に働くクーロン力は引力か斥力が求めなさい．

これはクーロン力の公式を使って，力の合成をすれば引力ですよね？

それで，(a,0)にある-qの電荷をx軸上で動かして引力から斥力に変わる座標を求めなさい．

という課題なのですが，どうしたらよいでしょうか．着目しているマイナス電荷のｘ座標をｘとしてクーロン力を関数としてらわして，正負の符号を調べようと思ったのですが１０次方程式になり行き詰ってしまいました．

そこで，直観的に考え，x<-aであれば斥力，-a<x<a, a<xでは引力ではないかと予想し，（多分そうだと思うのですが・・・）a<xにおいて，微分して単調増加を示そうかと思ったのですがこれもうまくいきませんでした．

新年早々ではありますが，宜しくお願いします．

yama さんのレス (2007/01/03(Wed) 23:31)

引力から斥力に変わる点では，力が 0 になるので，符号を調べなくても解けると思います． しかし計算はかなり面倒なものになりそうですね． もしかすると高次の項が消えて簡単な式になるのかもしれませんが・・・．

>直観的に考え，x<-aであれば斥力，-a<x<a, a<xでは引力ではないかと予想

この予想は当たっていないように思えます．

カリプソ さんのレス (2007/01/04(Thu) 17:44)

yamaさん返信ありがとうございます． ＞しかし計算はかなり面倒なものになりそうですね． もしかすると高次の項が消えて簡単な式になるのかもしれませんが・・・． 試してみますね．

カリプソ さんのレス (2007/01/06(Sat) 01:09)

>直観的に考え，x<-aであれば斥力，-a<x<a, a<xでは引力ではないかと予想

この予想は当たっていないように思えます．

とのことですが，解の範囲としては-a<x<0だけでしょうか？ それともa<xにもあるのでしょうか？

yama さんのレス (2007/01/06(Sat) 09:33)

ｘ軸の正の向きに十分遠く離れると斥力になることは分かると思います． 従って a<x の範囲に引力から斥力に変わる点があるはずです．

カリプソ さんのレス (2007/01/08(Mon) 22:30)

計算が上手くいかず，funvtion viewというそふとでグラフを描いてみたのですがa<xの範囲では負の値から単調減少しており解がありませんでした． 入力の仕方が悪いのかもしれませんがどうなんでしょうか．

CO さんのレス (2007/01/08(Mon) 23:10)

横から失礼いたします．

> 計算が上手くいかず，

計算を進める前の，一番最初の立式はどのようになりましたか？ そこが間違っていては元も子もないので，確認しておくべきだと思います．

yama さんのレス (2007/01/08(Mon) 23:21)

原点に +q の電荷があり，その近くに -q の電荷が３個あるわけですが，十分遠くから見るとこれらの電荷の位置の違いは無視できます．この場合，近似的に原点に -2q の電荷があると見なせます．その結果，十分遠くにある -q の電荷には斥力がはたらくことになります． x=a では引力なので，電荷を遠ざけていくとどこかで引力から斥力に変わるはずです． グラフを描いても解がなかったのは，入力した式が正しくなかったためではないでしょうか．

カリプソ さんのレス (2007/01/09(Tue) 00:52)

ご返答ありがとうございます．自分で立てた式を書いてみました．

x軸となす角をθと置くと，cosθ=x/(a^2+x^2) なので，クーロン力の合成のｘ成分f(x)=kq^2{2x/(x^2+a^2) +1/(x+a)^2 -1/x^2} となりました．それで，通分し，kq^2で割ったものの分子：g(x)は g(x)=2x^3(x+a)^2 -a(2x+a)(x^2+a^2)^3/2 となりました．ｘ→∞とすればg(x)は正だと思うのでどこかで負→正となるｘが存在するとは私も思うのですが．．．

グラフは，確かに入力ミスだったのですが，やり直してみると，単調増加はしているのですが0に収束するようなグラフになってしまいました．

ミュフ猫 さんのレス (2007/01/09(Tue) 01:23)

カリプソさんはじめまして

>f(x)=kq^2{2x/(x^2+a^2) +1/(x+a)^2 -1/x^2}

これがちょっと違うと思います． cosθ=x/√(a^2+x^2) ですから， f(x)=(kq^2)*{2x/(x^2+a^2)^(3/2) +1/(x+a)^2 -1/x^2} となるのではないでしょうか？

カリプソ さんのレス (2007/01/09(Tue) 02:02)

ミュウ猫さん，ご指摘ありがとうございます．そうでした．写し間違えました． g(x)の方は大丈夫だと思います．

ミュフ猫 さんのレス (2007/01/09(Tue) 02:20)

f(a)/(kq^2) =2a/(a^2+a^2)^(3/2) +1/(a+a)^2 -1/a^2 =2a/2√2a^3 +1/4a^2 -1/a^2 =1/√2a^2 +1/4a^2 -1/a^2 =(1/√2 +1/4 -1)/a^2 =(2√2 +1 -4)/4a^2 < 0

よって，点(a,0)では，引力（x軸の負方向の静電気力）ですよね？ じゃあ，a<xの範囲のどこかに負→正となるｘが存在するんじゃないでしょうか？

カリプソ さんのレス (2007/01/09(Tue) 03:09)

はい． ＞ｘ→∞とすればg(x)は正だと思うのでどこかで負→正となるｘが存在するとは私も思うのですが．．．

と前述はしましたが，g(x)＝０が解けないでいます．

ｙama さんのレス (2007/01/09(Tue) 08:58)

近似値でよければ，逐次近似法で求められると思います．

zoro さんのレス (2007/01/09(Tue) 12:53)

カリプソさん，始めまして．

最初に，問題を拝見したとき，x方向の力を出してみました．そして，その式で，座標xをaで割った式x'=x/aに変形しました．こうすれば，どんなaでも，しきにはaがなくなりますから検算が楽です．

具体的に計算するには，皆さんが仰っているのと同じで，原点近くと遠方の振る舞いからx'=1..2程度で力がゼロらしいと見て，エクセルで計算すると，1.03の近くで符号が反転するのが見られました．

＃この数値は，検算していないので，超参考値ですが．

この関数はスムーズな感じなので，手動でも1/1000のオーダなら，ステップを解の前後で1/10ごとに挙げれば答えが見つかるように思います．

勿論，ニュートン法などの逐次近似をするのもよいですが，「表計算＊人間ドライブ」も慣れておくと重宝しますね．

なんとなく さんのレス (2007/01/09(Tue) 13:23)

こんにちは，なんとなくです．

x=aでの引力が小さいので，斥力もa付近とみて，x=a(1+ξ）と置いて，ξの２次以上を無視すれば，概算でξ=(3-2√2)/(7-√2)=0.0307・・が得られました．zoroさんの結果とも整合するようですし，どうも1.033付近に解があるようですが，解析解は難しそうですね．そもそも解析解はあるのでしょうか？

カリプソ さんのレス (2007/01/13(Sat) 18:33)

yamaさん，１CO＠物理のかぎプロジェクトさん，ミュフ猫さん，zoroさん，なんとなくさん，返信ありがとうございます．

ふと，思ったのですが，解にはaという文字は関係してこないのでしょうか？

それと，ｘ＞a以外の範囲についても計算できないでいるのですが，ご教授いただけないでしょうか．

zoro さんのレス (2007/01/13(Sat) 19:06)

>解にはaという文字は関係してこないのでしょうか？

「aの何倍」みたいな言い方を出来ませんか．もしくは，「a=1」としてしまっても良いかもしれません．要は，計算が見やすく，簡単になればいいだけです．

問題を忘れかかっていますが，x軸に居る限り，電場はx軸だけの成分しか持ちませんね．

>ｘ＞a以外の範囲についても計算できないでいるのですが

ということは，計算している「電場はx軸の成分」を書き出してごらんになるとどうですか？ もし式に誤謬があれば，数値計算も正しくできませんよね．

たとえば，+qの電荷が(x,0)の場所にあって，

1. (-a,0)にある+qの電荷とつくる力F1
2. (0,0)にある-qの電荷とつくる力F2
3. (0,a)と (0,-a)にある+qの電荷と作るF3

これを書きますと共通して括れる量を括りだしてしまえば，いいと思います．

カリプソ さんのレス (2007/01/13(Sat) 21:58)

>「aの何倍」みたいな言い方を出来ませんか．もしくは，「a=1」としてしまっても良いかもしれません．要は，計算が見やすく，簡単になればいいだけです．

a=1とすると，funvtion viewというソフトでグラフを描くとx=1.03付近で負→正にいれかわりました．ということは皆さんa=1として計算しているということでしょうか？

a<x以外の範囲についても式はたてたのですが，＝０が解けないでいます．エクセルを使いこなせていないもので．．．

カリプソ さんのレス (2007/01/13(Sat) 22:05)

a=1とすると，funvtion viewというソフトでグラフを描くとx=1.03付近で負→正にいれかわりました．ということは皆さんa=1として計算しているということでしょうか？

と先程投稿しましたが，なんとなくさんのようにx=a(1+ξ）として考えているのですよね．．失礼しました．

zoro さんのレス (2007/01/13(Sat) 22:30)

> =a(1+ξ）として考えているのですよね．

これは正確に言えば，違うと思います．「x → x'*a とaを括りだす」と考え易いと思います．勿論，他の方々がどのように解かれてかは知りませんが．

何れにしろ，具体的に式を書き出せば，自ずとどうすれば善いかが明確になるとおもいますが．

> a<x以外の範囲についても式はたてたのですが，＝０が解けないでいます． 

この質問の意味が判りません．「ｘ＝０」の近傍は，-qの電荷に漸近するので発散するわけですよね．

「力＝０」の解の事ならば，ニュートン法などの解をだすサブルーチンを作る必要があるでしょう．それが嫌なら，近似の一段ごとの関数を書くか．何れにしろエクセルでは汎用の解法ルーチンを書くのは余程の準備がないと無理だと思います．

カリプソ さんのレス (2007/01/14(Sun) 00:17)

>「力＝０」の解の事ならば，ニュートン法などの解をだすサブルーチンを作る必要があるでしょう．それが嫌なら，近似の一段ごとの関数を書くか．何れにしろエクセルでは汎用の解法ルーチンを書くのは余程の準備がないと無理だと思います． 質問に不備があり申し訳ありません．力＝0のことです．ニュートン法等の近似計算を知らないのであります．

zoro さんのレス (2007/01/14(Sun) 01:45)

近似計算は，必要に応じて色々に求められると思います．

かりにある関数の解 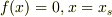を求めるとします．

この前後で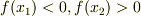， なら，少なくとも一つの解があるはずですね．

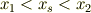
ここから段々と範囲を狭めていくのだって，立派な方法だとおもいますよ．挟み込み法とでもいえるかもしれませんね．

次の方法は，ニュートン法と言ったと思いますが，その関数の微分を使います．次の式を下の説明図 Aと比較すれば，何だこんな事かです：

これを整理して；

この式の右辺は 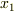での関数とその導関数の値だけです．従って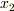， は1回目の逐次近似です．したがって，上の式(a)は逐次近似式であると考えられます．当然，逐次近似の次数は有限で切るわけで，近似解を得るという意味では，挟み込み法と大差ありませんし，微分が小さいと発散の危険性もあります．

ただ，プログラム作りの面でみれば，条件が強い分，条件別けを気楽にできるので，直ぐに書くには善いです．しかし，一般的に関数形を与えて解くような汎用ルーチンまで書こうとすると，一気に難しくなります．

<pre> 説明図 A ↑

｜ ｜ ｜ ｜ * f(x) ｜ * ｜ * ｜ * ｜ x1 xs * x2

−−＋−−−−−−−−+−−−+−−−+−−−−−−−−−−→x

｜ I * ／ ｜ I * ／ ｜ I * ／ ｜ I * ／ 傾き [df(x)/dx]x1 ｜ I * ／ ｜ I*／ ｜* f(x1) ｜ ／ ｜ * ／ ｜ ／ ｜

</pre>

なんとなく さんのレス (2007/01/14(Sun) 14:57)

>カリプソさん，なんとなくです． なかなか苦労されているようですが，問題を定性的に捉えておいででしょうか．答えはx軸上に2点あり，一点は(a,0)よりx軸正方向へ少し進んだところ，一点は(-a,0)と原点の中間より少し原点よりであると思います．おそらく解析的な解は求められないでしょう．定性的な解の検討は，私は以下のように考えました． (1) x=aで引力，x>>aで斥力（これはyamaさんに指摘されています）なので，x>aでひとつ解がある．しかもx=aの引力は（相対的に）値が小さいので，a付近に力の反転箇所がある． (2) 0<x<aでは，y軸上の2電荷-qによる斥力のx軸上の合計は原点に近寄るほど小さい．原点の+q電荷と(-a,0)の電荷-qによる力の差し引きは，逆2乗則により，原点に近寄るほど，引力の方がより大きく影響する．総合して，0<x<aでは引力は大きくなるばかりで斥力には変化しない． (3) -a<x<0では，(2)と逆に原点付近では引力が強く，(-a,0)に向かって，y軸上の電荷も(-a,0)の電荷も斥力が増大し，とくに-0.5aではx軸上の原点および(-a,0)の力が拮抗するため，y軸上の電荷による斥力の分，合計して斥力となっている．したがって，-0.5a<x<0の範囲，-0.5a付近に引力から斥力への反転解がある． (4) x<=-aでは(3)の考察により斥力となる． 答えの見当をつけて，zoroさんの書かれたニュートン・ラフソン法による計算を行う必要があります．というのは，ニュートン法は初期値が問題となるからです．検討を付けたあたりの数値から始めないと，別な解に落ちたり，収束しません．適切であれば10回程度のループで10^-6位の精度は得られます． それと，aの扱いはあまり気にしなくていいと思います．取り合えず１で置いても，後で定数倍だと思えばいいでしょう．

カリプソ さんのレス (2007/01/17(Wed) 23:56)

zoroさん，なんとなくさん，ありがとうございます． 皆さんから教えていただいたお陰で，なんとかまとめて提出することができました．これからまた質問することもあると思いますが，その時はまたよろしくお願いいたします．