斜面上の物体を引く力
斜面上の物体を引く力
seal さんの書込 (2006/12/27(Wed) 17:07)
はじめまして.高1のsealと申します. わからない問題があるので,教えていただきたいと思います.
【問題】 傾角αの斜面に質量mの物体を置いて,物体を糸で引く.引く力を最小にするには,どの向きに糸を引けばよいか.(斜面と物体の間の静止摩擦係数をμとする.)
/___糸 /θ 斜面\ ____
【考察】 図(見にくくてすいません)のように,糸を引く向きと斜面に平行な向きとのなす角をθにして,物体が動き出す直前の釣合の関係から,引く力fを求めてみました.すると,
f={(μcosα-sinα)mg}/(cosθ+μsinθ)
となりました.ここからどうすればいいかわかりません.そもそもfの値があってるかどうかもわかりません. よろしくおねがいします
Re: 斜面上の物体を引く力
CO さんのレス (2006/12/27(Wed) 21:25)
seal さん,こんばんは.
 の分子の
の分子の 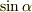 の符号が私のやったのと違いますが,他は一致しました.
機械的にやるならば微分してもできますが,高1 とのことなので別な方法を考えてみましょう.
の符号が私のやったのと違いますが,他は一致しました.
機械的にやるならば微分してもできますが,高1 とのことなので別な方法を考えてみましょう.
三角関数の合成はもう習いましたでしょうか? 三角関数の合成を行うと,
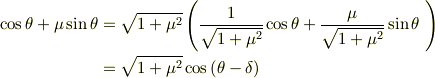
とかけます.ここで  は
は 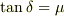 となるような
となるような  です.
です.
分母の値が大きければ大きいほど,  としては小さくなるので,
としては小さくなるので, 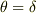 のところで
のところで  はもっとも小さくなるのではないでしょうか.
高1の問題としては難しいかもしれませんね.もっと簡単な方法があるのかもしれません.
はもっとも小さくなるのではないでしょうか.
高1の問題としては難しいかもしれませんね.もっと簡単な方法があるのかもしれません.
Re: 斜面上の物体を引く力
CO さんのレス (2006/12/27(Wed) 21:42)
あ,私は図を次のように書きました. 問題としてはどちらを意図しているんでしょうね. とりあえず,上の情報をもとにもう一度考えてみてください.
<pre> f ↑ θ| | |// / / </pre>
Re: 斜面上の物体を引く力
seal さんのレス (2006/12/28(Thu) 12:18)
coさん,返信ありがとうございます.
三角関数の合成はもう習いましたが,それを使うとは思いもよりませんでした.
問題に添えられていた図は,coさんの図のようではなく,糸で下側に引っ張られるような図になっていました.
fの値は,もう一度慎重に計算してみたいと思います.
ちなみに,微分を使ってもできると書かれていましたが,それはどのようにすればいいのでしょうか.一応,数?の微分までは知っています.この範囲で解けるのなら教えていただきたいと思うのですが・・・.
Re: 斜面上の物体を引く力
CO さんのレス (2006/12/28(Thu) 13:16)
> 問題に添えられていた図は,coさんの図のようではなく,糸で下側に引っ張られるような図になっていました.
なるほど,そちらでやったら seal さんの  と一致しました.
と一致しました.
> 微分を使ってもできると書かれていましたが,それはどのようにすればいいのでしょうか.
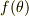 を
を  で微分してやり,増減表を書けば良いです.
で微分してやり,増減表を書けば良いです.
とりあえず一階微分を計算してみると
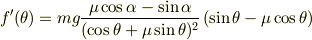
となります. 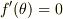 となる
となる  を求めると,
を求めると,
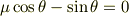
となります.これを満たす  が
が 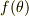 を最小(または最大)にします.
計算してみるとすぐにわかりますが,
を最小(または最大)にします.
計算してみるとすぐにわかりますが, 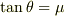 となるような
となるような  ということで,三角関数の合成から求めた結果と一致します.
ということで,三角関数の合成から求めた結果と一致します.
色々と細かい条件を省きました.正確な計算は seal さんがやってみてください. :)
Re: 斜面上の物体を引く力
seal さんのレス (2006/12/28(Thu) 16:47)
ありがとうございます.早速やってみます.
Re: 斜面上の物体を引く力
seal さんのレス (2006/12/30(Sat) 20:31)
f={(μcosα-sinα)mg}/(cosθ+μsinθ)を微分したら (df/dθ)=-(μcosα-sinα)mg(μcosθ-sinθ)/(cosθ+μsinθ)^2 となって,coさんと異なったんですけど…(マイナスの有無) どこかで間違ったのでしょうか?
Re: 斜面上の物体を引く力
seal さんのレス (2006/12/30(Sat) 21:30)
あと,増減表の書き方もよくわかりません.(θの範囲はどうすればよいのかとか.) おねがいします.
Re: 斜面上の物体を引く力
seal さんのレス (2006/12/31(Sun) 01:33)
そうでしたか. 増減表はあきらめて,第二次導関数を考えてみました.
g=f/{(μcosα-sinα)mg}=(cosθ+μsinθ)として,gをθで微分すると
dg/dθ=(sinθ-μcosθ)/(cosθ+μsinθ)^2
もう一回θで微分すると
d^2g/dθ^2={1/(cosθ+μsinθ)}+{2(μcosθ-sinθ)^2/(cosθ+μsinθ)^3}
よって,fをθで二回微分したものは
d^2f/dθ^2=(μcosα-sinα)mg[{1/(cosθ+μsinθ)}+{2(μcosθ-sinθ)^2/(cosθ+μsinθ)^3}]
これに,θ=tanインバースμを代入すると,
1/(μ^2+1)cos(tanインバースμ)
となって,これが正になることを示せればいいと思うのですが,わかりません おねがいします