電磁波

よこやり，すみません．yamaさんの説明は的確で正しいのですが，Jackさんは高校生ですよね．老婆心ながら，もしかするともっと基本的なところから説明が必要なのではないかと見受けられます．目に見えない，それも時空間的に変化する現象を文書で説明するのは難しいですが，どうしても個人のイメージに頼らざるを得ません．誰も実際の全体像を見た者はいないわけですし，そもそも見えませんからね．

物質（場）の形をちゃんと知りたいと思う心は大事です．私のイメージも完璧である筈が無く，それどころか間違っているかも知れませんが，書いてみますので，もし参考になれば嬉しいです．

まず，電（場）磁（場）を，「場」というときの物理的な意味は空間のある点で物理的観測が為される「実体」があることと考えたらよいでしょう．「実体」は目に見えることも見えないこともあり，間接的にしか観測できないこともあります．例えば，電場は電荷をそこ（の点）付近に置くと力を受けるような「場」(yamaさんが一度説明されましたね），磁場は磁石（厳密には磁荷は無いので）を置くと力を受けるわけです．「付近」と書いたのは，1点でのみ存在する「場」は考えないからです．通常の物理量は「場」も含めて時空間的に滑らかに連続していると思って（当面）差し支えないでしょう．力は方向と大きさがあるので「ベクトル」であることが分かります．これを「ベクトル場」と言います．

さて，電磁波を生じるもっとも簡単な素描はどのようなものでしょう．伸縮自在な小さな棒（重さや太さは無視できるとする）の両端に「＋」「−」の電荷が一つずつ着いているとします．棒は最初は長さがありますが，時間経過につれてどんどん短くなり，終には長さ０，そしてまた伸び始め，そのときは「＋−」の極が反転しているものとします．これを高速で繰り返す（振動すると言います）と，何が起きるでしょうか．高校でも学習するとおり，電荷「＋」から放射状に出た電気力線はあらゆる方向に出て，真上は無限遠に伸びますが，他はいつしか「−」極に吸い込まれるように入っていきます．このとき，電場はちょうど剥いたみかんの房のように或いは縦半分に切ったりんごのように芯を棒とした対称な楕円に似た線が幾層にも連なっている筈です．しかし，短くなると，中心付近の電気力線は開いた（閉じるとは一本の連続した線でつながること）部分が小さくなり，棒の長さ０で閉じた状態になります．なぜなら次の瞬間できる電気力線はそれまでと逆向きだから，場が連続しないからです．このとき，Jackさんの言われるような押し出しが生じると思えば良いでしょう．さて，このような簡単なモデルですが，電場はほぼ全方向に電気力線を結んでおり，０になるところが無いことが分かります．また，たとえ一様に振動していても，電気力線の形は刻々変化し，強さ（振幅）は棒の長さによるのでこれも振動していることが分かります．磁場は電場の振動によって誘導的に生じますが，電場が複雑な形なので磁場も同じです．もし棒の振動が正弦的であれば，棒＝０中心付近では加速度は最大となり上下につぶれた電気力線は指向性を持つことになります．ここで言う指向性は特定の向きに特に強く放射されるという意味で，その他の方向に全く放射されないわけではありません．この描像でなぜ全方向に電磁場があるか（特に真上，真下），遠方では上下に電磁場が（ほとんど）無いかイメージできますでしょうか．ここで，電（磁）場の強さは電気力線の密度に比例することを思いだせば，その強弱が将に波となって空間を伝播して行くのでしょう．長々，失礼しました．

Re: 電磁波

Jack さんのレス (2006/12/28(Thu) 04:58)

なんとなくさん詳しい説明ありがとうございます．

「棒＝０中心付近では加速度は最大となり」の「加速度」とは電気力線のことですか？

それと（ http://nkiso.u-tokai.ac.jp/phys/matsuura/lecture/general/presentation/Emwave/Emwave.files/frame.htm ）の14にある図では，波の山と谷の頂点は，磁場と電場それぞれどこになるのでしょうか？

Re: 電磁波

なんとなくさんのレス (2006/12/28(Thu) 10:22)

>Jackさん，こんにちは．

電気力線は実際の物理量ではなく，電場の状態を仮想的に表したものです．したがって電気力線が速度を持つとか加速度を持つという言い方は変です．私の描いたモデルでは電荷を動かして（振動させて）いますが，電荷の変化という意味での加速度です．つまり，棒中心では電荷の＋−が逆転する大きな変化があります．電場や磁場の強さは前記のように，そこに置いた電荷（磁荷）にかかる力の大きさで計られますが，電気力線で表すときは線の間隔が密なほど強く（山か谷），疎なほど弱いと約束することはご存知と思います．その図では明確ではありませんが，電場も磁場も粗密な力線の繰り返しであろうと思います．（しかし，電磁波が粗密波というのではなく，あくまでも振幅=強度が周期的であるということです）そして電場が最大なら磁場は最小，電場が最小なら磁場が最大というようにお互いのエネルギーを交換し合いながら，「あざなえる縄のごとく」進行していく，というイメージです．この最小がちょうど棒の中心のように変化が最大になる点で，電場と磁場が互いに誘導される最大の点であると思います．これは，電場から磁場が，磁場から電場が誘導されるとき，誘導される場の強さは，もとの場の強さのみではなく，その（時間）変化の大きさによるためです．

Re: 電磁波

ｙama さんのレス (2006/12/28(Thu) 14:39)

なんとなくさん，丁寧な説明ありがとうございます．しかし，ちょっと気になる点もあります．

>電場が最大なら磁場は最小，電場が最小なら磁場が最大というようにお互いのエネルギーを交換し合いながら，「あざなえる縄のごとく」進行していく，というイメージです．

私もそんなイメージを持っていたのですが，よく考えてみると違うようです．アンテナの近くは別として，アンテナから遠くはなれて平面波と見なせる場合は

http://upload.wikimedia.org/wikipedia/commons/3/30/Light-wave.png

の図のように，電場と磁場の最大・最小は一致しています．

>これは，電場から磁場が，磁場から電場が誘導されるとき，誘導される場の強さは，もとの場の強さのみではなく，その（時間）変化の大きさによるためです．

場の（時間）変化の大きさによって決まるのは，誘導される場の強さそのものではなく，誘導される場の回転です．たとえば磁場が正弦波として伝わっているとき，磁場が 0 のところで磁場の変化が最大になります．従って磁場が 0 のところで誘導電場の回転が最大になるわけですが，そのとき電場自体は 0 になっています．

Re: 電磁波

なんとなくさんのレス (2006/12/28(Thu) 21:46)

>yamaさん

こんにちは！コメント有難うございます．仰るとおりだと思います．電磁場の電場と磁場の振幅としての位相は私の説明ではπ/2ずれる印象を与えることには気付いていましたが，そのような図はあまり無いですからね．正直，言い過ぎなのですが，では本当のところはというと，私にも分かりません．確かにMAXWELL方程式から言っても時間変化は互いの回転に結びついているわけですから，実は最大になるのは回転であって，それをイメージすることは難しい．一方微分方程式の初期条件から考えれば，電場の発生時に磁場はなく，位相差が０であると結論づけるつよい根拠も思いつかないが，電磁波は発生した瞬間に光速度でなければならず，その世界は我々の静止系から時間軸に沿った観測は不可能であると思える．この辺り突き詰めれば最新の場の理論にも繋がりそうですが，間違っているかもしれないと思ったのも，この深さを感じたからなのです．

>Jackさん

というわけで，Jackさんの疑問はもっともだと思い，心惹かれて非力にも関わらず考えを聞いて頂いた訳です．これを明確に説明して下さる方がいれば嬉しいし，なければ，Jackさん，研究して解明してください(^^;)．

Re: 電磁波

Jack さんのレス (2006/12/29(Fri) 08:49)

お二人とも説明ありがとうございます．

>電荷の変化という意味での加速度

「加速度」は電荷の加速度のことだったんですね．

>その図では明確ではありませんが，電場も磁場も粗密な力線の繰り返しであろうと思います．

あの図では明確ではないんですか．分かりました．

他のあまり詳しい所は理解できませんでしたが^^；すみませんm(_ _)m

それから（ http://upload.wikimedia.org/wikipedia/commons/3/30/Light-wave.png ）この図は僕の学校の物理の先生も，電場が最小では磁場が最大のように半分ずれるはず，と言っていました．

Re: 電磁波

yama さんのレス (2006/12/29(Fri) 11:17)

電場と磁場の最大・最小の位置は一致していて，半分ずれることはありません．このことは，マクスウェル方程式に基づいて示すことができます．従ってその図は正しい・・・・と言いたいところですがよく見るとちょっと違っているようです．電場の向きが図の通りだとすると，磁場の向きは図とは反対になると思います．

Re: 電磁波

zoro さんのレス (2006/12/29(Fri) 12:14)

横から失礼します．

電磁気で起こる波は，電場と磁場が組み合わせて起こる波です．日常で見る波とは違い二重の波なので，直感的にイメージするのは難しいです．あまりに無理なイメージ作りに進まれないことをご推奨します．

私自身も，高校生の頃に，化学結合の仕組みが不思議で，先生に聞きに行きました．答えが得られるどころか，そんな馬鹿げた疑問を持つ前に，チャンと勉強しろと，おこられました．

>僕の学校の物理の先生も，電場が最小では磁場が最大のように半分ずれるはず，と言っていました．

このコメントは，半分正解で，半分不正解です．ｙamaさんが No.13386でコメントされているのが正しい理解だと思います．でもその解説でお若い方が理解できるかというと，それは不可能だと思います．そこで，私の個人的な考え方を書いて見ます．おそらく，若いときに拝見した，ファインマンさんのレクチャー・ノーツの電磁気学か，砂川さんの理論電磁気学がヒントになっているはずですが，両書とも手元にないので，参考意見程度にお読みください．

さて，電場と磁場は，真空中では；

・電場の回転 ∝ -磁場の時間変化 (ファラデイの電磁誘導) ・磁場の回転 ∝ +電場の時間変化 (アンペールの法則＋マクスウェルの変位電流)

真空中でしたら，・電場の発散=0 ・磁場の発散=0 も付帯するので，横波になります．

となります．この「回転」というのはベクトル解析の知識がないと理解し難いのですが...．

＃そういう意味では複雑ですが，水面に立つ波の解析も，＃流体力学をフルに用いて計算する時には，＃高校や教養の物理での波の話のようにスラスラとは出ません．

しかし，今のようにz軸の方向に進む波に限定すると式が簡単になります．本来は電場や磁場は3次元のベヴェクタですが，横波の為に，z方向の成分は取れず，電場と磁場も直交します．簡単の為に，電場はx軸，磁場はy軸を向くと考えることが出来ます．すると電場や磁場の成分を，波の関数f(kz-ωt)で表せます．この波の関数f(kz-ωt)は位置の関数(z)と同時に時間の関数(t)によって電場と磁場が協調して進むのだと思います．丁度，海で周期的な波の波頭が進んでいる風景を電場なり磁場と重ねあわせてイメージするとよいかも知れません．

上に表した波の関数f(kz-ωt)には面白い性質があります．zの偏微分とtの偏微分が比例することです．以下の説明は，数学的に厳密ではありませんし，高校の先生に助けてもらってください．

天下り的に変数グザイを定義します．

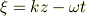
$\xi = kz- \omega t$

この全微分を考えると；

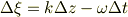
$\Delta \xi = k\Delta z- \omega\Delta t$

ここで波の関数 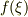$f(\xi)$ を考えると，変数グザイが一定ならば，波(の関数)も一定です．そこで波の一定となる条件は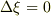， $\Delta \xi=0$ と考えられますから，

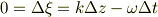
$0=\Delta \xi = k\Delta z- \omega\Delta t$

は，波の進む速さを出していると考えられます;

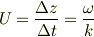
$U= \frac{\Delta z}{\Delta t} = \frac{\omega}{k}$

こんどは，波の関数自体の全微分を考えます；

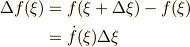
$\Delta f(\xi) &= f(\xi + \Delta \xi) -f(\xi) \\&= \dot f(\xi) \Delta \xi$

ここで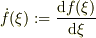， $\dot f(\xi) := \frac{\mathrm{d} f(\xi)}{\mathrm{d} \xi}$ です．

要は，波の関数は 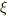$\xi$ を通してだけ変化するから，各偏微分は；

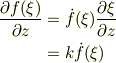
$\frac{\partial f(\xi)}{\partial z} &=\dot f(\xi)\frac{\partial \xi}{\partial z} \\&=k\dot f(\xi)$

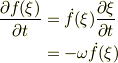
$\frac{\partial f(\xi)}{\partial t} &=\dot f(\xi)\frac{\partial \xi}{\partial t} \\&=-\omega \dot f(\xi)$

従って，

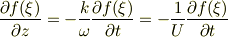
$\frac{\partial f(\xi)}{\partial z}=-\frac{k}{\omega}\frac{\partial f(\xi)}{\partial t} = -\frac{1}{U}\frac{\partial f(\xi)}{\partial t}$

と成ります．

＃もったいぶって波の速さをUとしましたが，＃光も電磁波の一部なので，U→c と書くと... .

驚くべきことに，回転(今のばあいzの偏微分)と時間変化(tの偏微分)とは相互に，比例関係を示してしまいます．途中端折っていますが，電場，磁場の方向成分について子のような関係があるので，最終的に電場ベクタと磁場ベクタは直交して，すなわち直線偏光を示しながら，+z方向，これも電場ベクタと磁場ベクタとの外積方向に進むということが出来ます(説明は略)．

以上が荒ぽく平面波の挙動を私なりに書き下してみたものです．正確ではありませんが，雰囲気がわかればと思いました．

アンテナ周辺の話を書いたのですが，図形表示を入れると，段落が乱れるので，別記します．

＝＝＝＝＝

これらの現象を，ｙamaさんは No.13386で簡潔に述べられているので, 引用させていただきます：

ーーーー引用開始

ーーーー引用終了

あるレベルに達すると，言葉による再整理は，現象の把握に役立つと思います．しかし，逆に初心者の方に言葉だけで説明し切るのは，誤解を受けたり，同道周りをする危険性があると思います．

むしろある種の関連性元に，数学モデルを交える方が良い場合が多いようにも思われます．もちろん，私は教育の経験が無いので，無責任な発言の可能性もあるので，ご注意願います．

Re: 電磁波

zoro さんのレス (2006/12/29(Fri) 12:47)

【図が入ると乱れるようなので，手動で改行を入れています．】

アンテナ周辺の挙動は，とても難しく，簡単なイメージは破綻すると思います．もう少し，電磁気や計算手法を学ばれてからトライすることをお勧めします．

でも，ある種のイメージを作るだけなら簡単な方法があると思います．「マクスウェルの変位電流」を有限面積の並行コンデンサに適応して考えることです．

丁度，ある時刻まで電荷が無い所に，電圧をかけて電荷がコンデンサに流入していく過程を考えます．電荷が流入する以上，コンデンサの中間部にも電流が流れると考えたいですよね．

それが<b>変位電流</b>と考えていいと思います．

<pre> 図1 幅の狭いコンデンサの側面図・電流の注入 | ↓I(t)=dQ(t) / dt +Q(t) | 電極A --------------------------- ↓ 電場なし ↓ 電場＋変位電流 ↓ ---------------------------電極A' -Q(t) |

</pre>

次に，そのコンデンサを並行から段々と広げていきます． <pre> 図2 その下の電極を不均一に広げた．

電流の注入⇒アンテナの給電線・ |↓I(t)=dQ(t)/dt +Q(t) | 電極A ---------------------------

電場が外に出てくる！変位電流も外に出てくる！ _--------電極A'' _------- ｜ _----- </pre>

そして，最後には,天地が逆になってしまいまいましたが，ダイポール型アンテナのできあがり．

<pre> 図3 極限として両電極を直線状に配置した．

アンテナの給電線

|
|
|
|
|
|

電極A--------------------------- ---------------------------電極A'''

</pre>

電流の電線内部での分布も時間の関数にして考えていく必要があります．でも，そこまでしないとアンテナの機構を正しく扱えませんが，そんなこと知らなくてもラジオ，テレビそして携帯電話もつかえる時代ですよね．

もし必要ならば，電磁波の解析プログラムも一杯あると思います． (携帯電話や電子レンジの開発で多用されていると推察します．

けれど本質的な理解は，マクスウェル方程式群と，波動解の幾何学的理解で十分なような気がします． <pre>

というように考えると如何でしょうか？

【ヘルプ】

編集画面では，可笑しな事をしてないはずですが，どうしても横長になります．修正法をご存知でしたら，教示くださいませんか？

Re: 電磁波

yama さんのレス (2006/12/29(Fri) 23:18)

No.13386 は，なんとなくさんに宛てて書いたものなので，高校生に分かるような書き方はしませんでした．きちんと説明するためには，ベクトル解析とかマクスウェル方程式などの説明も必要になると思いますが，高校段階ではそれはちょっと難しいと思いました．従って，当面は結論だけ受け入れてもらって，詳しいことは大学などで学んでもらえばいいと思ったわけです．しかし，もちろん高校生に分かるように説明できればそのほうがいいと思いますので，zoro さんの説明によって理解されることを期待します．

Re: 電磁波

zoro さんのレス (2006/12/30(Sat) 00:38)

yamaさん，

>従って，当面は結論だけ受け入れてもらって，詳しいことは大学などで学んでもらえばいいと思ったわけです．

最初の質問の頃は，私もそう思いました．しかし，その後の Jackさんの質問のあり方を拝見していると，とても強い疑問が繰り返し出てくるように感じました．このような状態であれば，高校生さんとして説明するよりは，未知の分野を探求する仲間の一人として遇し，自分なりの考えをぶつけていくのも可能かと思いました．

＃マクスウェルの方程式群を示し，＃波動解としての進行速度と角振動数と概念を説明する事にして見ました．＃それには陰関数の微分の説明を要しました．

これを機に，物理の基本をじっくりと身につけるには，数学の基本も必要だし，それがわかると，逆に波動現象を共通の現象として捕らえることが出来る事を知って欲しいです．

こんな説明は自分の頭の中にしか無く，通常の高校教育から逸脱しているだろうと思います．是非とも，高校の先生と論議できる環境の様ですので，批判的にご討議いただければ幸いです．

「電磁気現象は摩訶不思議ではなく，マクスウェル方程式群を数学的な裏づけの基に段階を追って行けば，誰でもが同じ結論を得られるのだ」という点を若き学徒の皆さんに認識いただきたいと思います．と同時に，より善い解釈があれば，是非ともお教えくださると嬉しいです．

Re: 電磁波

Jack さんのレス (2006/12/30(Sat) 10:34)

はじめにアンテナの図を載せましたが，アンテナから出ている電磁波でなくともいいのですが，どちらにせよ今の知識ではきちんと理解出来なさそうなので，勉強してから改めて読ませて頂きます．

丁寧な説明してくださっているのに理解できなくてすみません．

それからyamaさんzoroさん，しつこい質問に答えて頂いてありがとうございました．

Re: 電磁波

zoro さんのレス (2006/12/30(Sat) 17:47)

Jackさん，

今は，基礎，特に数学や英語をガッチリ固めながら，かつ，自分なりの疑問を膨らませて行くと，ダイナミックな勉強になると思いますし，第一，面白いですよね．

＃ただ，専門馬鹿には注意してくださいね．＃それなりに，わが国の文化・歴史について把握して置くとよいでしょう．

>丁寧な説明してくださっているのに理解できなくてすみません．

こちらこそ，説明力が足りずに御免なさい．今回の経験を踏まえて，数学的な説明を段階を踏まえて，判り易く波動の関数の性質を表現するをトライしたいなと，思います．それに波の関数も

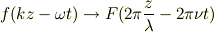
$f(kz-\omega t) \to F(2\pi \frac{z}{\lambda}-2\pi \nu t)$

とか，さらに「f, Fを余弦関数，正弦関数に書いてしまった方が判り易かったか」と反省しています．

私は，若い頃，「数学は道具だ」と思い，正面きって勉強しなかった(できなかった)為に，ズバリと表現ができません．中期的な展望で，取り組みたいと思います．

お互い，歳も環境も違いますが，大いに全力を尽くしたいですね．

Re: 電磁波

yama さんのレス (2006/12/30(Sat) 18:21)

少しずつ段階的に理解していくことが大切だと思います．その過程で疑問点が出てきたらまた質問してください．

Re: 電磁波

Jack さんのレス (2007/01/04(Thu) 01:19)

はい．アドバイスありがとうございます．

英語はかなり苦手ですが（笑）

返信遅れてすみませんでした．

[home] [掲示板] [ページの先頭]