えり さんの書込 (2006/12/22(Fri) 17:32)

こんにちは．問題を解いていてわからなかったので質問させていただきました．

「2s[m]離して張った十分長い２本の平行導線がｚ軸に平行に固定されていて，これに?[A]の同じ大きさの定常電流がｚ軸の正の向きに流れている．導線の太さおよび地磁気の影響は無視できるものとし，真空の透磁率をμとして，次の問いに答えよ．ただし解答はs,?,y,μを用いて記せ．

点Ｍ(s,0,0)と点Ｎ(-s,0,0)を通る2本の導線の電流が点Ｐ(0,y,0)につくる磁束密度の成分Ｂx,Ｂy,Ｂz［T］を求めよ．」

という問題で，y,z成分がOになるのがどうしてなのかわかりません．教えて下さい．

zoro さんのレス (2006/12/22(Fri) 18:03)

ズボラな説明をして見ます：

無限の長さの導線がつくる磁束密度は，ｚ方向の対称性から導線の方向の成分を持ちません．従って，z方向の成分は初めからゼロとしていいですね．

＃と書きましたが，ビオ・サバールの法則で，電流に垂直な成分しかない，というほうが素直だと思います．

また，無限の長さの導線がつくる磁束密度は考える点から導線に垂線を下ろした時の半径の円上では，全て同じ大きさを持ち,その方向は円の接線方向方向です．そこで，今の場合，+z方向から，z=0での断面,xy平面で作図すれば，其々の導線が作る磁束密度のベクトル和は，...．

toorisugari no Hiro さんのレス (2006/12/22(Fri) 20:21)

えりさん: 「 z軸上の無限に長い直線の上に一様な電荷が分布しているとき， (1) 電場 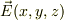はzに依存しない( 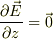)ことを示せ． (2) 電場 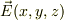のz成分は0であることを示せ． 」 という問題はわかりますか?(積分とか使わないで，絵で理解できれば十分です．)

えり さんのレス (2006/12/23(Sat) 00:12)

>zoro様

>無限の長さの導線がつくる磁束密度は，ｚ方向の対称性から導線の方向の成分を持ちません．

そうでしたよねっ．うっかりしてました…

>今の場合，+z方向から，z=0での断面,xy平面で作図すれば，其々の導線が作る磁束密度のベクトル和は，...．

>その方向は円の接線方向方向です

あ，そうするとy成分も0になりますね！！どうもありがとうございました！よく覚えておきます(>_<)

>toorisugari no Hiro様

えーと，電荷がz軸上に沿って一様に分布していたら，z軸方向には電気力線が出て行かないから，z方向の成分が0で，z軸に依存しないという考えではだめでしょうか…