背理法
背理法
はる さんの書込 (2006/12/21(Thu) 15:36)
はじめまして,高校三年生です. 数学での質問なのですが,先日背理法の勉強をしていたとき, 背理法と対偶証明法は少し違う,との記述があったのですが, 具体的にどこが違うのかどなたか教えて頂けないでしょうか?
Re: 背理法
zoro さんのレス (2006/12/21(Thu) 16:33)
はるさん,はじめまして.
yahooで「背理法 対偶証明法」というサイトがありました.
・ http://www.geisya.or.jp/~mwm48961/koukou/cond004.htm
ご存知でしたら御免なさい.
====
このサイトは高校の教育レベルを知る上でも中々興味深いものがあるようです.
Re: 背理法
はる さんのレス (2006/12/21(Thu) 21:56)
zoroさん,そのサイトに行ってみました. 先に,背理法は証明したいことの余事象は正しくない事を示してから・・・の流れのようですが, 結局対偶証明法と同じのような気がしてしまうのですが・・・ 私の頭が至らないようですね(笑)
Re: 背理法
zoro さんのレス (2006/12/21(Thu) 22:16)
このサイトは,最近の高校生さんたちがどのような数学を学ばれているか解って面白かったです.
私は物理も落ちこぼれていますが,数学はもっと落ちこぼれナノで,このサイトを見ても「背理法 vs 対偶証明法」の違いが解りませんでした.
どうしても判りたい問題があるなら,それを書いてしまえば,どなたかが答えて下さるだろうと思いますが....
Re: 背理法
はる さんのレス (2006/12/22(Fri) 14:48)
いえ,特にわからない問題がある,というわけでもなく, なんとなく気になっていたのです. 今度予備校で聞いてみようと思います.ありがとうございました.
Re: 背理法
yama さんのレス (2006/12/22(Fri) 15:26)
対偶証明法とはその命題の対偶を証明することです.命題とその対偶は同値なので,対偶が証明されればもとの命題が証明されたことになります. それに対して,背理法は,命題を否定すれば矛盾が生じることを示すものです.
例えば, 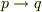 という命題を証明するとします.
という命題を証明するとします.
対偶証明法では, 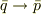 を証明します.そのためには
を証明します.そのためには 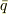 を仮定して
を仮定して 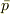 を導くことになります.
を導くことになります.
背理法では 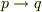 の否定を仮定して矛盾を導きます.
の否定を仮定して矛盾を導きます. 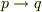 の否定は 「
の否定は 「 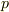 かつ
かつ 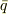 」 なので,
」 なので, 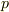 と
と 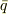 の両方を仮定して矛盾を導くわけです.矛盾というのは,具体的には
の両方を仮定して矛盾を導くわけです.矛盾というのは,具体的には  とか
とか  のような仮定に反する命題,あるいは公理に反するような命題が導かれることです.
のような仮定に反する命題,あるいは公理に反するような命題が導かれることです.
つまり,次のようにまとめられます.
対偶証明法 :  だけを仮定して
だけを仮定して 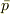 を導く.
背理法 :
を導く.
背理法 : 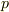 と
と 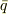 の両方を仮定して矛盾を導く.
の両方を仮定して矛盾を導く.
しかし,場合によっては背理法の一部として対偶証明法が用いられることがあります.
というのは,背理法の仮定のうち 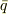 だけを用いて
だけを用いて 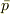 を導くことができれば,これはもう1つの仮定の
を導くことができれば,これはもう1つの仮定の 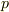 に反することになるので矛盾が生じたことになります.この場合,「
に反することになるので矛盾が生じたことになります.この場合,「 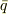 だけを用いて
だけを用いて 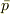 を導く」というのは対偶を証明することになります.
を導く」というのは対偶を証明することになります.