mie さんの書込 (2006/12/17(Sun) 00:22)

磁束密度を求めるもんだいで

半径aの円形断面を持つ無限に長い導線（円筒形）を考え電流Iの定常電流が円筒形の軸の方向に一様にながれている．

?導線「内外」の磁束密度を求めよ．

半径aの円形断面を持つ無限に長い導線（円筒形）を考え，その表面に面電流密度J（向きは円筒形の軸方向）流れている．

?この「周り」に生じる磁束密度を求めよ．

この「内外」と「周り」の違いがよくわかりません．「周り」は「外」とかんがえてよろしいのでしょうか？？

zoro さんのレス (2006/12/17(Sun) 01:00)

mieさん，始めまして．

(1)の問題は，円形断面の中が詰まっていて普通の導線で，電流は円の断面を均一に流れる，だから（円筒形）では無いのでは？

(2)の問題では，表面だけに電流が流れる，だから円筒形なのでは？

なんとなく さんのレス (2006/12/17(Sun) 09:36)

横やり失礼します．

>zoroさん 「円筒」は中身が詰まっている，円柱の場合もこう呼ぶことがあります．

mieさん，初めまして． (1) の問題は，zoroさんの言われるように，断面を平均的に流れる電流により 作られる磁場で，円筒内部と外部では違う式になります． (2) の問題は厚さの無い円管に電流が流れるイメージなのですが，この問題では 外部（周り）の磁場しか問うていないのだと思います． それと，(1)では電流，(2)では面電流密度ですから，自ずと解答に差がでます．

mie さんのレス (2006/12/17(Sun) 09:49)

zoroさん申し送れましたが，こちらこそはじめまして．

早速の返信ありがとうございます．

zoroさんの考えを参考させてもらいます！

?導線の周りに半径ｒの同心円を考え，平曲線Cを考える（向きは右ねじの法則を利用）?はCに沿った積分

無限に長い導線なのでアンペールの法則を利用する

?B・ｄC＝B?ｄC＝B・２πｒ＝μ₀I

∴B＝μ₀I/２πｒ

?全電流をI＝πa²Jと考える．?同様に問題をとくと

B＝μ₀πa²J /２πｒ

↑のようなとき方でいいのでしょうか？

mie さんのレス (2006/12/17(Sun) 09:54)

あれ・・・・文字化けしてる・・・．&#8320は「ちっさい０」，&sup2は「二乗」ですね・・・．

なんとなくさんはじめまして！返信ありがとうございます．

ということは上の式まちがっているかもしれないですね・・もう一度かんがえてみます！

mie さんのレス (2006/12/17(Sun) 11:19)

全角英数字はベクトルと考えてください．

?対称性から，磁束密度Ｂは導線に垂直な平面内にあって，磁束密度は導線の中心軸周りに同心円をえがくので，中心軸のまわりrの円周cについて，アンペールの法則をてきようすると

円周が導線内にあるとき（r＜a）

?Ｂ・dＣ＝2πrB＝μI(r/a)2←r/aの２乗，μはμゼロ

∴B＝μrI/2π(a)2←aの２乗，μはμゼロ

円周が外側にあるとき（r＞a）

同様にアンペールの法則をもちいて

B=μI/2πr ←μはμゼロ

ということですね！

なんとなく さんのレス (2006/12/17(Sun) 11:57)

それで，いいんじゃないでしょうか． r<aのとき，r〜aの残りの部分からの寄与は対称性からキャンセルすることになりますが，少し計算は面倒です．もし，そこまで求められているなら，厳密にはキャンセレーションを証明しなければならないでしょうが，問題ではそこまでしないでしょう．

zoro さんのレス (2006/12/18(Mon) 14:50)

mieさん，

>2006/12/17(Sun) 11:19 No.13275

で，回答を得られたと思った居ました．

ただ，表式の「下付きの添え字」で苦労されていたのに今気が付きましたので，コメントします．

μ ₀

これは下記のように書きます．(S → s）とすれば，上のようになります． μ<Sub>0</Sub>

ついでに， x ^-2

x<Sup>-2</Sup>

です．

もしLaTeXをお使いになれるなら，

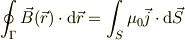
上の式も，下の原稿で，T → t とするだけで書くことができます．

<Tex> oint_{Gamma} vec B(vec r)cdot mathrm{d} vec r = int_{S} mu_{0} vec j cdot mathrm{d} vec S </Tex>

以上，記法の話だけでした．