プランク放射法則による太陽黒点の温度

h-yama さんの書込 (2006/12/16(Sat) 08:12)

高校の地学教師です．太陽のCCD画像を使った教材を考案しています．

特定波長で撮像した太陽のＣＣＤ画像で，静穏部と黒点暗部の輻射強度Ｒ0,Rの比較から，静穏部の温度T0を元に，黒点暗部Tを求める教材を作りたいと思っています．プランクの放射法則を使えばよいということはわかるのですが，各部で成り立つ， R(λ)=37418/{λ^5(exp(14388/λT)-1)} の式を使って，R0,RとT0，Tの関係式を作りたいのですが，行き詰まっています．お教え願えませんか．よろしくお願いします．

Re: プランク放射法則による太陽黒点の温度

yama さんのレス (2006/12/16(Sat) 17:46)

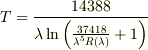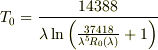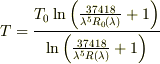
R(λ)=37418/{λ^5(exp(14388/λT)-1)} より $T=\frac{14388}{\lambda\ln\left(\frac{37418}{\lambda^5R(\lambda)}+1\right)}$ となり，同様に $T_0=\frac{14388}{\lambda\ln\left(\frac{37418}{\lambda^5R_0(\lambda)}+1\right)}$ となるのでＴは次のように表されると思います． $T=\frac{T_0\ln\left(\frac{37418}{\lambda^5R_0(\lambda)}+1\right)}{\ln\left(\frac{37418}{\lambda^5R(\lambda)}+1\right)}$

Re: プランク放射法則による太陽黒点の温度

h-yama さんのレス (2006/12/16(Sat) 20:32)

yamaさま早速の回答ありがとうございまさす．一度試してみます．また，ご指導よろしくお願いします．

Re: プランク放射法則による太陽黒点の温度

yama さんのレス (2006/12/16(Sat) 23:40)

よく考えてみると，上記の式はあまり役に立ちそうにありません．というのは，R(λ)を求めるには，CCDの特性や大気による光の吸収も考慮しなければならないのですが，特に後者を正確に見積もるのは難しいからです．

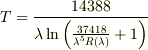
しかし，R(λ) と R0(λ) の比はCCDのデータから簡単に求められると思います．その比の実測値を α とすると，R(λ)=αR0(λ) となります．また，R0(λ) は温度 T0 を用いて次のように表されます． R0(λ)=37418/{λ^5(exp(14388/λT0)-1)} 従って，R(λ)=αR0(λ)=37418α/{λ^5(exp(14388/λT0)-1)} となります．この R(λ) を用いれば，温度 T は次の式で表されます． $T=\frac{14388}{\lambda\ln\left(\frac{37418}{\lambda^5R(\lambda)}+1\right)}$

Re: プランク放射法則による太陽黒点の温度

h-yama さんのレス (2006/12/20(Wed) 23:06)

ｙａｍａさま，ありがとうございます．

確かに，前回の式ですとCCD画像のR(λ) と R0(λ) の比と太陽の静穏領域のR0(λ)の値が必要になってきますね．ところで，R(λ)=37418/{λ^5(exp(14388/λT)-1)}の式で，波長λの単位はｍで良いのでしょうか？今，使っているデータではλ＝656.8*10^-9 ｍでαの値が0.2038です．定数の37418や14388はプランク分布式の2hc^2と hc/kの定数部分だと思うのですが．

Re: プランク放射法則による太陽黒点の温度

yama さんのレス (2006/12/21(Thu) 00:18)

14388 がhc/kの定数部分だとすると，波長の単位はmではなくて μm になると思います．しかし，37418 がよくわかりません．2hc^2 ではこの数字にはなりません． 2πhc^2 かもしれません．

Re: プランク放射法則による太陽黒点の温度

h-yama さんのレス (2006/12/21(Thu) 20:21)

ややこしくて申し訳ありません． α＝0.20378，T0＝5800，λ＝0.6538μｍで計算しみました．計算を間違えていなければ，T=1.678E+03となって，オーダーは合って来ました．ただ，黒点暗部のTは4000〜5000Kくらいですから，だいぶ小さく出います．定数部の37418ですが，元のプランク分布式は B(λ,T) = (２hc^2／λ^5)×｛１／（exp(ｈｃ／λｋT)−１)｝です．

Re: プランク放射法則による太陽黒点の温度

zoro さんのレス (2006/12/21(Thu) 20:51)

横から失礼します．

理化学辞典，第3版，プランクの放射法則よると，絶対温度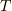で放射平衡にある黒体から放出される放射のうち波長が 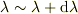$\lambda \sim \lambda + \mathrm{d}\lambda$ にある放射エネルギ密度を 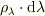$\rho_{\lambda}\cdot \mathrm{d}\lambda$ とすると；

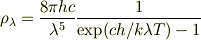
$\rho_{\lambda} =\frac{8\pi hc}{\lambda^{5}}\frac{1}{\exp (ch / k \lambda T) -1}$

とありました．ご参考まで．

追伸：

急に心配になり，いくつか見てみると，結構食い違いがあるようですね．

http://en.wikipedia.org/wiki/Planck%27s_law_of_black_body_radiation

とは一致しました．物理の話を多数決で判断するのはいけないとは思いますが(笑)．

Re: プランク放射法則による太陽黒点の温度

h-yama さんのレス (2006/12/21(Thu) 21:47)

ZOROさんコメントありがとうございます．

先ほどの計算（No.13315）は少し間違っていました．やり直したところ，T=4.240E+03という値が出て来ました．この値だとほぼ良い値かと思います．なお，定数部の37418ですが，計算の中で約分されしまいます．λ^5も同様に約分されます．もう少し丁寧にチェックしてみます．

Re: プランク放射法則による太陽黒点の温度

zoro さんのレス (2006/12/21(Thu) 22:10)

>定数部の37418ですが，計算の中で約分されしまいます．λ^5も同様に約分されます．

やはりそうですか．てっきり，独立した2波長のデータをつき合わせるのだろうと思っていました．

面白そうなテーマだと思うので，巧くいったらウェブ・サイトに乗せられると良いですね．

Re: プランク放射法則による太陽黒点の温度

yama さんのレス (2006/12/21(Thu) 23:58)

プランクの放射式は普通zoroさんが書かれた式で表され，係数は8πhcですね．ただしこれは黒体放射で満たされた空洞内のエネルギー密度です．今問題にしているのは放射されるエネルギーの流れの密度なので，単位時間に単位立体角に放射されるエネルギーの流れの密度を求めるとすると，体積密度に c/4π を掛けることになり，その結果係数は 2hc^2 になると思います．しかし 37418 という値はこの π倍になっているようです．その理由はよくわかりません．いずれにしても，約分されるのでこの値自体は今の場合問題にならないでしょう．

λ^5 も約分されますが，式中にはなお λ が残るので，異なる波長についても観測して比較してみるとおもしろいと思います．

Re: プランク放射法則による太陽黒点の温度

zoro さんのレス (2006/12/22(Fri) 16:27)

yamaさん，

>今問題にしているのは放射されるエネルギーの流れの密度なので，単位時間に単位立体角に放射されるエネルギーの流れの密度を求めるとすると，体積密度に c/4π を掛けることになり

なるほど，エネルギ流失速度と体積密度との差でしたか．太陽の場合，放射立体角は半空間に限定されるので， c/2πの方が良いような気がしますが．

むしろ，以前にお書きになった； >R(λ)を求めるには，CCDの特性や大気による光の吸収も考慮しなければならないのですが

を追求する必要があるかなと思っています；

大気の問題は，十分に晴れて，雲による影響が排除されていれば，大気による吸収効果は予測可能な気がします．
残りは, 検出側の波長特性，バンド幅などを含めた受像側の問題になろうかと推察します．

＝＝＝＝

h-yamaさん，

上のように考え出すと，どの様にデータを収集されているかに興味が湧いてきました．望遠レンズに強い波長制限をするフィルタを付けて太陽を撮影されるのでしょうか？また，VTRなどで取るとすると，どの様に追跡するとか．

もし宜しければ，解説くださると嬉しいです．

Re: プランク放射法則による太陽黒点の温度

yama さんのレス (2006/12/22(Fri) 22:54)

確かにいろいろ検討を要する問題はありますね．ところで，波長は No.13310 では λ＝656.8*10^-9 ｍ，No.13315 では λ＝0.6538μｍとなっていますが，どちらが正しいのでしょうか．もし前者だとしたら， Hα に近いので，水素の吸収線の影響でプランクの式からのずれが生じるのではないでしょうか．

Re: プランク放射法則による太陽黒点の温度

h-yama さんのレス (2006/12/22(Fri) 23:26)

yamaさまzoroさま

いろいろありがとうございました．おかげさまでようやく，まともな値が出てきました．観測設備が揃っておらず，自分での観測はできていません．また，普通の望遠鏡では，筒内の散乱光でなかなかまともな値が出てきません．もともと，天文学の専門観測画像を使って，高校生のための実習教材を作るのが目的です．本来なら高校の地学の教科書にも出てくる，Eの４乗則を使って黒点暗部の温度を求めたかったのですが，とりあえず手に入るFITS画像でNASAの太陽観測衛星SOHOの画像と国内天文台の太陽望遠鏡DSTの同日の同じ黒点のFITS画像を使うことなりました．これらの画像は特定の波長を使った単色画像なのでプランク分布式を使う必要が出てきたわけです．２日分の画像からDST4.1*10^3K，SOHO：4.6*10^3KとDST:4.3*10^3K，SOHO:4.6*10^3Kの値が出ました．何とか教材化のメドが立ちそうで，本当に感謝しています．なお，さらに詳しい事がご入り用でしたら，ｈ−ｙａｍａ＠ｂｉｗａｋｏ．ｊｐにご一報をおねがいします．