微分

Joh さんの書込 (2006/12/13(Wed) 02:56)

掲示板のみなさまには，いつもお世話になります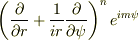． $\left( \frac{\partial}{\partial r} + \frac{1}{ir}\frac{\partial}{\partial \psi} \right) ^{n} e^{im\psi}$ というｎ階微分を，nとmの漸化式の形にしたいのですが，一般項がうまく求められません．私の計算力不足が原因とは思いますが，みなさまのお知恵を拝借したく存じます．自分で手計算してみた部分だけ参考に書いておきます．

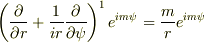
$\left( \frac{\partial}{\partial r} + \frac{1}{ir}\frac{\partial}{\partial \psi} \right) ^{1} e^{im\psi} = \frac{m}{r}e^{im\psi}$

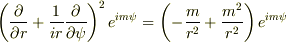
$\left( \frac{\partial}{\partial r} + \frac{1}{ir}\frac{\partial}{\partial \psi} \right) ^{2} e^{im\psi} =\left( -\frac{m}{r^{2}} + \frac{m^{2}}{r^{2}}\right) e^{im\psi}$

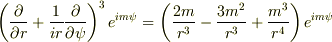
$\left( \frac{\partial}{\partial r} + \frac{1}{ir}\frac{\partial}{\partial \psi} \right) ^{3} e^{im\psi} =\left( \frac{2m}{r^{3}}-\frac{3m^{2}}{r^{3}} + \frac{m^{3}}{r^{4}}\right) e^{im\psi}$

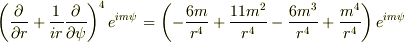
$\left( \frac{\partial}{\partial r} + \frac{1}{ir}\frac{\partial}{\partial \psi} \right) ^{4} e^{im\psi} =\left( -\frac{6m}{r^{4}}+\frac{11m^{2}}{r^{4}} - \frac{6m^{3}}{r^{4}}+\frac{m^{4}}{r^{4}} \right) e^{im\psi}$