流体力学 境界層について
流体力学 境界層について
アオイ さんの書込 (2006/12/11(Mon) 16:46)
茶碗の中のお茶にスプーンを入れ,かき回してお茶に回転運動を与える.次にスプーンを取り出しお茶をそのまま放置する.お茶はしばらくの間回転し続けるが,このとき茶碗の底に沈んでいるお茶の葉の運動を観察すると,お茶の葉は,お茶の回転運動が止まるころ,中央付近に集まることをがわかる. この現象を境界層の概念から説明せよ.
という課題が出されたんですが境界層と関係があるのかどうかすらわかりません. 説明できる方いませんか??おねがいします!! ちなみに明後日までの課題です(泣)
Re: 流体力学 境界層について
toorisugari no Hiro さんのレス (2006/12/11(Mon) 19:13)
有名なアインシュタインの問題ですね.(真偽は不明ですが,サロンでご婦人に質問されたアインシュタインが,はじめてこの問題を境界層で説明したと言われています.)
答えを教えるのは好きではないのでヒントとして,問題をだします.
- 茶碗の壁から遠いところ(境界層外)では流体は円運動(剛体回転)していますが,流体と一緒に動く系から見ると,力が釣り合っています.何と何の力が釣り合っていますか?
- 茶碗の底の境界層は薄いので圧力分布は上部の(境界層外の)圧力分布と同じと考えられます.しかし,何かが上部の境界層外とは分布が違っています.それは何ですか?(境界層の内部で急激に変化するのは何でしょう?)
- その結果どんな二次的な流れが発生しますか?
Re: 流体力学 境界層について
zoro さんのレス (2006/12/11(Mon) 23:22)
横から失礼します.
流体力学は不得意なので,ティーバックの滓(カス)を取り出して水に混ぜて攪拌して見ましたが,綺麗に「滓の饅頭」が形成されるもので,思わず拍手してしまいました(笑).
でも,すこし詳しく見ると面白いことが判りました:
(1)強くかき混ぜた後,中央が凹みますが,空気や泡を吸い込み易く,中央部に滓のほとんど無い部分が出来ます.でも大部分の滓は全体的に分布しています.
(2)少しすると,外側から滓が集合始めますが,中央部の空白部分は結構残って,台風の目のようにも見えます.
(3)さらに外側が集合を強め,急に中央部が潰れ,全体もぎゅっと饅頭型に変形して終わる感じです.
どなたかVTRをお持ちの方がいらっしゃれば,撮影して下さると面白そうですね.良く知られたことだったら御免なさい.
Re: 流体力学 境界層について
toorisugari no Hiro さんのレス (2006/12/12(Tue) 10:56)
zoroさん おもしろい実験ですね.
(1)で「強くかき混ぜる」ことを一定のペースで円を描くように長い時間(10秒から20秒)やってみてください.(余り強すぎない方がうまくいくかも.またスプーンより棒の方がいいかも)
その後はどうなりますか?
Re: 流体力学 境界層について
zoro さんのレス (2006/12/12(Tue) 12:29)
アオイさん
流体力学の話の腰を折る積りは在りませんので,ドンドン質問をお続けください.
====
toorisugari no Hiroさん
少なくとも,昨晩の観察では;
・ガラスのコップ:内径6.8cm,水の高さ5cm ・攪拌棒:フォークで幅2cmぐらい,ステンレス製
でした.
>スプーンより棒の方がいいかも
に従って,OHPペンに変えて見ましたが,この方が混ぜ易いようです.またプラスティック製の為に,容器の底に押し付けて,回せるので安定しているようです.
一寸やっただけでは,差異が見つからなかったので,もう少しサイズの大きな容器でテストしてみようと思います.
なお,冷静にテストしてみると,水面の凹形状は,意外と早くフラットに戻るのに気が付きました(笑).
Re: 流体力学 境界層について
toorisugari no Hiro さんのレス (2006/12/12(Tue) 13:50)
早速実験ありがとうございます.
水面のへこみですが,2種類あるのではないのでしょうか. (1) 全体が放物面をえがいてへこむ.(至る所下に凸) (2) 中央に「えくぼ」状のへこみができる.(水面は下に凸な領域と上に凸な領域に分かれる.)
zoroさんの最初の実験は(2)に相当するものではないかと予想しているのですが.
Re: 流体力学 境界層について
toorisugari no Hiro さんのレス (2006/12/12(Tue) 16:09)
> (2) 中央に「えくぼ」状のへこみができる.(水面は下に凸な領域と上に凸な領域に分かれる.)
この書き方はまちがいですね.
- 中央に「えくぼ」状のへこみができる.
にしておいてください.
Re: 流体力学 境界層について
zoro さんのレス (2006/12/13(Wed) 00:00)
この様なナイーブな実験は,結構難しいですね.
第一,手で回すのが難しい.回転速度は2Hzぐらいですが,一人だと計数できない. 第二,どうしても「小泡」が出てきて,中心部に集まる為に,中央の窪みが判らない.
でした.また,もう少し直径や深さを変えたいのですが,忙しくて探しにいけませんでした.
面白いことは,丁寧にかき混ぜて見ると,攪拌棒を引き上げた瞬間に,中央に出来る空白部が無いのですが,一寸すると出てくるのです.きっと数秒のことだとは思いますが.
実験者は目視に気が取られるので,時間感覚がとても低下するようです.
水面の大雑把な局面を計算してみました.いま,一定の角速度  で水が回転すると近似するとして,その水と一緒に回転する座標で,動径方向r,垂直方向zとして,ある半径r,水面の高さzでの接線は,そこの部分に作用する体積力:重力gと遠心力
で水が回転すると近似するとして,その水と一緒に回転する座標で,動径方向r,垂直方向zとして,ある半径r,水面の高さzでの接線は,そこの部分に作用する体積力:重力gと遠心力 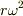 の合力;言い換えると見かけの重力に垂直であることから;
の合力;言い換えると見かけの重力に垂直であることから;
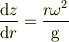
辺々を  に付いて積分すれば,中心からみた高さは;
に付いて積分すれば,中心からみた高さは;
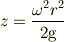
現在の設定では,
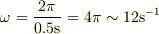

これらから概算すると
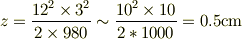
この程度では,直線形蛍光灯などの像が見えたり,歪曲して見えなくなった程度しかわかりません.
それにしても中央に発生する「滓の少ない部分」がどうして出来るのだろうか?感触では,中央の上部から「滓より比重の少ない水」が中心点に落下するように見えるのだが.
ヒョットすると,コップの壁面から固体-液体の相互作用を通して,外側から段々に回転速度を減少する為に,擬似重力が内向きに戻り,それと共に「比重の大きな滓」は下方・中央に掃き寄せられ,その逆に「比重の少ない水」が上方・外側に集まり,表面がフラットに成る時に中央に落ち込むのではなかろうか?
=====
他方,外壁に接した液体は静止するとなると,短い距離ながら,壁の近傍で高さの勾配が見られるはず(中心と同じ高さのはず)ですが,そんな気配は全くありません.どうしてでしょうかね?
Re: 流体力学 境界層について
toorisugari no Hiro さんのレス (2006/12/13(Wed) 02:09)
実験ご苦労様です. ううむ.なかなか,やっかいな(=おもしろい)事になってきましたね.
とりあえず,わかるところだけ
> 他方,外壁に接した液体は静止するとなると,短い距離ながら,壁の近傍で高さの勾配が見られるはず(中心と同じ高さのはず)
回転しているなら,遠心力は外向きですので,圧力は半径方向に非減少です.よって壁近傍でも表面の勾配が反転することはありません.
> 面白いことは,丁寧にかき混ぜて見ると,攪拌棒を引き上げた瞬間に,中央に出来る空白部が無いのですが,一寸すると出てくるのです.きっと数秒のことだとは思いますが.
中央の空白部は謎ですね.私は全体が剛体回転しておらず中央の近傍だけが剛体回転しているせいだと思ったのですが,自信がなくなってきました.
#この近所に地球流体屋さんはいないのでしょうかね.
Re: 流体力学 境界層について
Joh さんのレス (2006/12/13(Wed) 02:10)
私が学生のときは,陶芸用の回転ロクロで実験しました. Eckmann layerで検索するといろいろ分かると思います.
Re: 流体力学 境界層について
toorisugari no Hiro さんのレス (2006/12/13(Wed) 02:12)
中央の空白部って単に上昇流が卓越してるので,滓がとどまっていないと言うだけかも.
Re: 流体力学 境界層について
アオイ さんのレス (2006/12/13(Wed) 04:46)
むむむ・・・よくわかんないです.話が難しすぎて,「???」って感じです. ヒントをみても,聞いてもそれすらわからないバカ学生なんで泣
Re: 流体力学 境界層について
zoro さんのレス (2006/12/13(Wed) 11:07)
> アオイさん >ヒントをみても,聞いてもそれすらわからない
私もまったく同感です.流体力学には,何重もの不可思議があり; ・式が判り難く, ・「固体面に流体が静止」するという分子運動的に理解し難い仮定が鎮座して, ・その上,2D,3Dの解になるという.
真っ当な素人では,判らない方が自然だと思います!
そこで,割り切って実験をスタートさせました.むしろ,判らないだらけですので,質問をされた方がいいように思います.
Re: 流体力学 境界層について
toorisugari no Hiro さんのレス (2006/12/13(Wed) 14:55)
アオイさん: 「わからない」ってだけでは何もお手伝いできません.
アオイさんがレポートを作成するお手伝いはできても,代わりにレポートを作ることはできないのですから.ここがわからないとか具体的な質問をされれば,お答えできると思います.
zoroさん:
たしかに流体力学って難しいですよね.Navier-Stokes方程式は単に 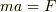 にすぎないのに何故ああも数学的に難しいのでしょう.
にすぎないのに何故ああも数学的に難しいのでしょう.
ところで, > ・「固体面に流体が静止」するという分子運動的に理解し難い仮定が鎮座して,
これって理解しがたいでしょうか?
量子論を忘れてるし,すこし嘘がある説明ですが,私は以下のように理解しています.
「
(1) たとえゆっくり(ex. 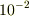 m/s)動いてる空気でも分子は音速(
m/s)動いてる空気でも分子は音速( 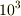 m/s)に近い速さでランダムに動いている.
m/s)に近い速さでランダムに動いている.
- (静止している)壁は拡大するとゴツゴツしていてその表面の法線ベクトルはランダムに分布している(と考える).
- 空気分子が壁に衝突するとき,壁の表面がランダムなので乱反射され,その方向は(流体側を向いた)すべての方向に分布している.(嘘あり)
- 速度
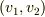 (
( 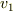 は壁に平行,
は壁に平行, 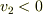 は壁に垂直,な速度成分)で壁にぶつかる粒子の反射された速度の「統計平均」は
は壁に垂直,な速度成分)で壁にぶつかる粒子の反射された速度の「統計平均」は 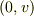 に近い形になる.つまり壁に平行な運動量成分は「平均として」壁に奪われる傾向がある.(量子論的・統計力学的にもっとまっとうな説明もあるそうです.)
に近い形になる.つまり壁に平行な運動量成分は「平均として」壁に奪われる傾向がある.(量子論的・統計力学的にもっとまっとうな説明もあるそうです.) - すなわち壁に平行な速度成分が「平均として」あっても,運動量が壁に奪われ,直に「平均として」0になる.(分子一個一個には平行な速度成分(
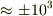 m/s)はあるが平均すると0になる.)
m/s)はあるが平均すると0になる.) - 気体の平均自由行程,及び,音速から導かれる長さ,時間のスケールより大きいスケールで観測したとき壁に接した流体の速度は0とみなせる.
- 粘性がないときは,流体の変形速度に制限はないので,「壁に接した部分だけ止まっていて,壁からちょっとでも離れると主流の速度に復帰する」と考えて良い.(壁近傍の流体は激しく横方向に引き延ばされるが流体は気にしない.)
(8) 粘性があるときは,流体は素早い変形(引き延ばし)をいやがるので,壁に近い部分の流体も引っ張られて減速する.壁からある短い長さの領域の部分で流体の速度は0から主流の速度へと急激に変化する.この領域を境界層という. 」
と言う感じです.(一応アオイさんの質問につながるように配慮しました.(笑))
Re: 流体力学 境界層について
zoro さんのレス (2006/12/14(Thu) 01:15)
アオイさん
時間切れかも知れませんが,手持ちの本:
流体力学,神部 勉・編著,石井 克哉・共著,裳華房,ISBN:4-7853-2063-X
のp191, コラム「紅茶の葉 と 流体力学」に図が載っていて,おそらくtoorisugari no Hiroさんの解説に近いように感じました.ご参考まで.
#今頃,手持ちの本に気づいたという,お馬鹿さんな私.
toorisugari no Hiroさん
これまで,気体分子運動論は考えても,液体分子運動論的な解釈をまじめにしたことがない事に気が付きました.ご解説を念頭に置き,しばらく勉強したいと思います.
特に,液体と固体表面の相互作用のイメージを明確に出来れば,自信をもって流体力学を勉強する元気が手に入りそうな予感がします.この面で,ご推奨の参考書をご存知でしたら教えて頂けませんか?
Re: 流体力学 境界層について
Joh さんのレス (2006/12/14(Thu) 01:36)
zoroさん>
液体と気体の違いは,Knudsen数の差だと思います. 固体壁との相互作用に興味があるならば,
の第一章が参考になると思いますが.
Re: 流体力学 境界層について
toorisugari no Hiro さんのレス (2006/12/14(Thu) 02:14)
> 液体分子運動論的な解釈をまじめにしたことがない事に気が付きました.
実は意識的に避けていました.
> 液体と気体の違いは,Knudsen数の差だと思います.
そうでしょうか?マクロで見たときには液体も気体も定性的な区別はないですが,ミクロでは運動量の輸送のメカニズムが,気体とは違うのではないのでしょうか?
たぶん,液体はまだ余りわかってないのじゃないかな?(自信なし)
Re: 流体力学 境界層について
Joh さんのレス (2006/12/14(Thu) 02:42)
>ミクロでは運動量の輸送のメカニズムが,気体とは違うのではないのでしょうか?
そうかもしれません.私の認識不足です.分子的に見たとき,運動量輸送のシステムというのは,流体分子間では衝突によるのだと思いますが,衝突自体はだいたい剛体衝突と見て,問題は平均分子行程と三体衝突以上の多体衝突があるか,というような点なんだと思います.(全然自信なし.)そんなつもりでKnudsen数と書きました.気体と液体で違いが顕著なのは,境界条件だと思います.マクロに言えば粘性ということなんでしょうが,私は鏡面反射とマックスウェル反射しか知りません.液体分子の壁面との相互作用は,どんな点が重要なんでしょうか?
Re: 流体力学 境界層について
zoro さんのレス (2006/12/14(Thu) 02:45)
Johさん,ご意見を感謝します.
>液体と気体の違いは,Knudsen数の差だと思います.
toorisugari no Hiroさんの解説の一部がこれだった訳ですね.素人の不勉強で,レイノルズ数しか頭に入っていなかったので,この観点もスコープに入れます.
>固体壁との相互作用に興味があるならば, > http://www.asakura.co.jp/books/isbn/4-254-13653-6/ >の第一章が参考になると思いますが.
なるほど,「分子気体力学」とは...,「Boltzmann方程式」に巡りあうとは思いませんでした.使えるようになるのに時間が掛かりそうなのが怖いです(笑)が,本屋さんで眺めてから考えて見ます.
それにしても「7.付録II直接シミュレーション法」まであって,気迫が感じられます.
Re: 流体力学 境界層について
toorisugari no Hiro さんのレス (2006/12/14(Thu) 03:32)
Johさん
私は液体は(も)全く知りません.
> 私は鏡面反射とマックスウェル反射しか知りません.
よろしければマックスウェル反射についてポインタを教えてもらえないでしょうか?
> 問題は平均分子行程と三体衝突以上の多体衝突があるか,というような点なんだと思います.
「平均分子行程」って液体であるのかよくわかりませんが,「多体衝突」が本質なんじゃないかなと,素人考えですが,おもいます.
Re: 流体力学 境界層について
Re: 流体力学 境界層について
toorisugari no Hiro さんのレス (2006/12/14(Thu) 04:51)
ティーカップの問題ですが,アインシュタインは確かにこの問題の最初の研究者で回答者だけど,「境界層」と言う考えは彼の論文からは伺えなかったと言う記事が, 英語ですけど,
に書いてありました.
Re: 流体力学 境界層について
zoro さんのレス (2006/12/14(Thu) 20:50)
> http://www.physicstoday.org/vol-59/iss-10/p10.html
に出ていた,エクマンの厚さ;
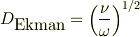
を求めて見る事にします.
水の動粘性係数, 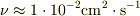
水の回転角速度は,12/13(Wed) 00:00 No.13169 より, 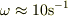
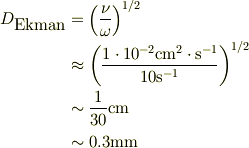
となり,境界層の厚さは意外と薄いのですね.従って,境界層を経由して滓が移動するのは,回転が速い場合は,層が薄すぎて移動できないと思います.棒を抜いて書く速度は十分の1程度に減速すれが, 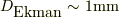 程度になり,中央に移動できるのかも知れません.
程度になり,中央に移動できるのかも知れません.
ただ,自分の目には,境界層を経由して滓が移動しているとは見えませんが....
ご紹介のサイトにある3番目の参考文献;
「Einstein, Ideas and Opinions, Crown Publishers, New York (1954), p. 250.」
図書館などで見てくれる方がいらっしゃいませんか?
Re: 流体力学 境界層について
Joh さんのレス (2006/12/15(Fri) 00:36)
>よろしければマックスウェル反射についてポインタを教えてもらえないでしょうか?
私のあやしい理解では,鏡面反射はビリヤードの玉のように入射角と反射角が同じような反射,マックスウェル反射は,壁面と流体粒子の相互作用が十分にあり,反射後の放出される角度が,全方位について正規分布のようになるようなものだったと思います.いま手元に参考書が無いので,正規分布という部分は,非常にアヤシイです.この二つの混合反射というのもあったと思います.
>「平均分子行程」って液体であるのかよくわかりませんが,「多体衝突」が本質>なんじゃないかなと,素人考えですが,おもいます.
私はいまだに,理想的な連続体という非圧縮流体のイメージと,分子がどれくらいの隙間でおしくらまんじゅうしているのか,というイメージにギャップがあります.液体の場合には,どんな場合でも隣の分子と接しているんでしょうか?(それがKnudsen数の極限という意味ではあるわけですけど...)
難しいです.
Re: 流体力学 境界層について
toorisugari no Hiro さんのレス (2006/12/15(Fri) 02:22)
> マックスウェル反射は,壁面と流体粒子の相互作用が十分にあり,反射後の放出される角度が,全方位について正規分布のようになるようなものだったと思います.
なるほど,前の説明で使った反射は実はマックスウェル反射だったのですね.(汗)
乱反射(あるいは複数回の乱反射)ではねかえるか,壁分子に束縛され他の壁分子と多体的に相互作用したあとはねかえるか,解釈はいろいろあるでしょうが,その過程により反射されることをマックスウェル反射というのですね.
ありがとうございます.
液体は....本当わかりません.
Re: 流体力学 境界層について
zoro さんのレス (2006/12/15(Fri) 11:43)
自分のコップと神部さんの流体力学の本を横目に,仕事をしていると,仕事になりません(笑).
で,思いついたのは,「境界層を無しにした実験」をすれば攪拌の問題が大幅に改善できそうだ,ということです.すると,急に,Johさんが書かれていた;
> 私が学生のときは,陶芸用の回転ロクロで実験しました.
が気になりました.でも,この実験は,「言うは易し,行なうは難し」のような気がしますが;
- 定常状態をつづけると,水に分散した微粒子は中央に集まりましたか?
- ロクロに制動を掛けるとどうなりましたか?
- もし宜しければ,実験条件を教えていただけますか?
- さらに宜しければ,実験した時の考察をお教えくださると嬉しいです.
> Eckmann layerで検索するといろいろ分かると思います
今,気が付いたのですが,「Ekman」ではありませんか? それなら多数ヒットしますが,これから見てみます.
Re: 流体力学 境界層について
Joh さんのレス (2006/12/15(Fri) 11:49)
zoroさん,
エクマンのつづりは自信ありません.たくさんヒットする方が正解ではないでしょうか.いい加減なことを書いてすみません.
ロクロの実験は,なにぶん大昔のことなので,(そしていやいや出席していた学生実験だったので)細かい状況は何も覚えていません(汗).実験条件は,洗面器に水と浮きを入れ,浮きと洗面器の印が同調するまでロクロに載せて放っておき(つまり定常状態です),そのあとお茶の出がらしを入れたような気がします.
Re: 流体力学 境界層について
zoro さんのレス (2006/12/15(Fri) 17:59)
>たくさんヒットする方が正解ではないでしょうか
どうやら海流と風との関係の解析が多いようでした.そこで「Ekman layer teacup」だと近いものが出て気ますが,細かく解説したのが見当たりませんでした.もうすこし検討を続けます.
>ロクロの実験は,なにぶん大昔のことなので,(そしていやいや出席していた学生実験だったので)細かい状況は何も覚えていません(汗).
学生実験は,学生の工夫などの余地が少ないので,味気ないです.予算も人も足り無いからとは思いますが.
>実験条件は,洗面器に水と浮きを入れ,浮きと洗面器の印が同調するまでロクロに載せて放っておき(つまり定常状態です),そのあとお茶の出がらしを入れたような気がします.
こういう何気ない方法で定常状態を出すのもなるほどです.「紅茶袋の滓」を「お茶の出がらし」すると,サイズ効果を見ることが出来るかも知れないので,やってみます.
Re: 流体力学 境界層について(ろくろの実験)
zoro さんのレス (2006/12/29(Fri) 14:24)
昨日,よい子の「紅茶の滓」実験を,他の素材でテストしようと思い東急ハンズに行きました.その折に,「簡易ロクロ」見たいなものあります?と聞いたら,「ろくろ倶楽部」という商品(税込み10500円+DVD・筆・エプロン付き)を紹介され,つい購入してしまいました.
これで,内径12cm強の容器を回したところ;
- 初めに棒でかき混ぜていても,直ぐに外周部の縁に集結してしまいます.
(2) 回転のSWを切っても, (2a)ゆっくり速度が下がり,ドーナッツ状(盛り上がり直径5cm, ドーナッツの幅1cm)になります. (2b)手で制動を掛けると,一挙に収縮し,饅頭形に集合します.
回転速度は0.6〜0.7回転/s ですが,この手の実験には十分な気がします.
でも,境界層の厚みと微粉末の粒径との関係などを実験するには,速度のダイナミック・レンジを拡大したり,回転数の直読などの工夫が欲しいところです.
良い子の流体力学演習にも最適ですよ.自分では,流線型でない鈍い形状の応答を検討してみたいと思っています:「流れるプール」での実験として考えようと....
もし,正当な流体力学的手法により,ガッチリと解析が出来る方がいらしたら,詳しい解析方法を開示していただけないでしょうか?