みちるさん さんの書込 (2006/12/11(Mon) 00:53)

交流電源，コンデンサ，電気抵抗がこの順で直列に並んでいる回路があります．

ここで，出力は電気抵抗の電圧の絶対値とします．

この回路に対する微分方程式を解くことは普通にできるのですが，周波数を変化させたときの出力をパソコン（実験で，NeXTのSPICEを使いました）でシュミレーションし，両対数の軸でグラフ化すると，

「一次関数的に斜めに進んでから，周波数がある程度大きくなると，あとは真横に進む」

みたいな感じの絵になるんです．

…何故ですか？

周波数を１０倍１００倍と変化させる様子を見ようとしてこのグラフを作っているのでしょうが，周波数を変化させるのですから，出力電圧が「真横に進む」なんてことはありえず，アップダウンするような気がするんですが．

そして私の最大の疑問は，時間tの扱いです．先ほどの位相の話に関連しますが，周波数特性というのはもちろん横軸を周波数として推移を調べようというものなのでしょうが，時間ｔによっても色々と変化すると思うのですが．ｔもひとつのパラメータですよね．なのに，そんなことはお構いナシに，先ほど述べたようなグラフが現れてきました．もしかして，「時間が十分経ったとき」とかを仮定しているんですか？それなら，微分方程式の指数関数の項が消えるというメリットはありますが，三角関数の位相はωによってかなり変化すると思います．

少々表現力に乏しい質問となってしまいましたが，よろしくお願いいたします．

なお，参考になるかどうかは分かりませんが，電源の最大電圧は５V，コンデンサの電気容量は1μF，電気抵抗は1kΩです．

CO さんのレス (2006/12/11(Mon) 20:22)

> この回路に対する微分方程式を解くことは普通にできるのですが

とりあえず微分方程式の解を示して下さい． それを見ながら考えましょう． :) については時間平均をとるんじゃないでしょうか．

ken さんのレス (2006/12/11(Mon) 22:23)

NeXTをお使いとは，ひょっとしたら私の卒業した大阪府にある 某独立法人大学かもしれませんが．

あまり，難しく考えないほうがいいです． 微分方程式はとりあえずおいといて， 電源の実効電圧をE，コンデンサの電気容量をC，抵抗値はRとしましょう． （↑ちょっと変えました．ご注意を） コンデンサのインピーダンスが 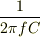で書けるのは いいですよね． は電源の周波数です． 抵抗にかかる電圧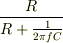は， です． この式は 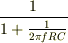ともかけます． ヒントはここまで．後は考えてみてください．

みちるさん さんのレス (2006/12/14(Thu) 21:38)

texが使えないかと試してみましたが，不慣れなもので，うまく動作してくれませんでした．ｗ

ＣＯさんには申し訳ありませんが，この文体で方程式の解を説明させていただきますと，

Ｒ（指数関数＋sin＋cos）の形で，

eの指数は-1/CR + A（A：初期条件から求まる定数）

sinの係数はVRω^2C^2/(R^2ω^2C^2+1)，位相はωt

cosの係数はVωC/(R^2ω^2C^2+1)，位相はωt

となりました．

kenさんの方法で考えますと，確かに周波数fが大きくなれば抵抗電圧は収束します…が，kenさんの式だと分母と分子で次元が一致してしまいませんか？

電圧をかければよいのだと思いますが，この場合は…Vsinωtですよね．この電源電圧を比例配分すると考えれば．

ただ，インピーダンスというのは私の頭の中では複素電圧だとか複素電流だとかを考えるときに使える道具であって，時間変化を追うときにそれを抵抗とみなして一瞬で求めてしまうのはなんだか変だ，というような思い込みがあるんですよね．

本題に戻りますが，Vsinωtという三角関数がくっついてくるとなると，やはり振動を起こすのではないでしょうか．

それにしても，高校のときから未だに交流系を完璧に理解した気になれません．

もうひとつ蛇足ですが，恐らくkenさんのおっしゃるとおり，わたくしも吹田の某大学の人間です．w

ken さんのレス (2006/12/15(Fri) 23:14)

こんばんわ

>kenさんの式だと分母と分子で次元が一致してしまいませんか？ 電圧をかければよいのだと思いますが

Eを分子にかけるのを忘れていました．

>本題に戻りますが，Vsinωtという三角関数がくっついてくるとなると，やはり振動を起こすのではないでしょうか．

それは，元が交流電源なので，そうです．

ところで，みちるさんはフェ―ザー法の知識がありますか？

みちるさん さんのレス (2006/12/16(Sat) 10:11)

すみません，ないです……．

あ，今調べてみたところ，名前は知らなかったんですが，この方法は知っています．

アレですよね，コンデンサのインピーダンスとコイルのインピーダンスをそれぞれ

1/iωC，iωLと考えて，複素数のまま解を出して，最後にsinかcosかどっちかの成分をとるという．

この方法で解いてもよいのですが…担当の先生が「微分方程式を解け」みたいな指示を出したんです．

どうすればよいでしょうか．

ken さんのレス (2006/12/16(Sat) 22:53)

一般的には >この方法で解いてもよいのですが…担当の先生が「微分方程式を解け」みたいな指示を出したんです． であれば，先生の指示には逆らうなということでしょう．

「この回路に対する微分方程式を解くことは普通にできる」 ということなので，多分その解は B sin(ωt+φ)のかたちになるかと思います． （なってないのであれば，適当にφをおいてこの形にする） するとBはωの関数になっているはずです． tの関数にはなっていないはずです． Bがωによってどうなるかをみればいいです．

みちるさん さんのレス (2006/12/17(Sun) 11:40)

係数については処理できました．確かに収束します．

ただ，φはωが増えるにつれて０に収束する（と思われる）ので，sinの中身にωが入っている以上，０になったりプラスになったりマイナスになったりするはずなんですが…．

あ…もしかして，両対数グラフだと，そんな振動はほとんど表現されないんですかね？

ken さんのレス (2006/12/17(Sun) 21:18)

解はB sin(ωt+φ)のかたちになったのですよね． SPICEが表すのは振幅部分のBとφです． （設定によってはBではなくBをもとの電源電圧で割った比ですが）

振幅Bと横軸の周波数f それに位相遅れφがわかれば 時間方向の式B sin(2πft+φ)が出せます． シミュレータで知りたいのは周波数に対するBの値と φの値（こっちは知らなくていい場合が多いですが） だけなのでそれしか表示しません．

みちるさんはシミュレータ(SPICE以外であっても)が B sin(ωt+φ)を表示するものと思っているかもしれませんが， そうではなくBを計算し表示するものです．

おっと，これは周波数特性解析の話で（もとがそうだから） トランジェント解析の場合は別です． 詳しいことは，シミュレータの解説書を読んでください．