困っています…．

運動量が保存するので，分裂前の物体の運動量から，分裂後の一方の物体の運動量をベクトル的に差し引いたものが，分裂後のもう一方の物体の運動量になります，従って，大きさ20×10のベクトルから，それに垂直で大きさ10×5のベクトルを差し引けばいいわけです．それを質量で割ったものが速度です．図を描けば用意に求められるはずなのでやってみてください．なお，向きは初めの速度の方向に対する角度をθとして tanθ の値で表すといいでしょう．

Re: 困っています…．

なんとなくさんのレス (2006/12/03(Sun) 17:48)

この問題．成立しますか？どこかおかしい気がしますが． yamaさんの数字も問題と逆ではないですか．

Re: 困っています…．

yama さんのレス (2006/12/03(Sun) 17:57)

数値を間違えていました．大きさ20×5のベクトルから，それに垂直で大きさ10×10のベクトルを差し引くというのが正しいです．この場合，速度の向きは角度の値自体で表せますね．

なんとなくさんのご指摘の件ですが，問題としては成立すると思います．なんとなくさんは運動エネルギーが保存しないことをおかしく思われたのかもしれませんが，爆発によって分裂する場合はエネルギーが保存する必要はないと思います．というよりも，運動エネルギーの保存を要求すれば分裂は不可能になると思います．

Re: 困っています…．

なんとなくさんのレス (2006/12/03(Sun) 18:15)

>yamaさんわたしもそれは考えました．しかし，問題として適切かどうかは疑問な気がしますね．所謂，問題の為の問題設定というか，逆にこのような状況を実現するには極めて微妙な爆発が必要であり，運動量が保存する保障もないわけです． yamaさんに文句を言っても仕方ないし，言うつもりもないですが．その意味で，この問題ってどうなんでしょう？

Re: 困っています…．

yama さんのレス (2006/12/03(Sun) 18:28)

厳密に言えば，火薬の爆発で分裂する場合は，爆発で生じるガスの運動量も含めないと運動量の保存は成り立ちませんが，それは無視するということでしょう．あるいは，押し縮めておいたバネの力で分裂するということも考えられます．この場合は運動量は正確に保存すると思います．

Re: 困っています…．

なんとなくさんのレス (2006/12/03(Sun) 19:02)

論点がずれている気がしますが．勿論バネであるとか，あるいは複合粒子で有れば結合エネルギーの開放であるとか，理論上の可能性のことでなく（成立という言葉が悪かったかも知れませんが）ずれていないとすると，「この問題自身には何も問題はない」とお考えということでしょうか．私は「問題設定が不自然過ぎて不適切で問題有り」と思う，ということです．もっとも，この問題自身がそういう「問題点」を考えさせるような意図ならばまた別の論点もでて来ますが．大仰に言えば，この「かぎしっぽ」が物理のおちこぼれを自称し，物理を好きになって貰うような初志を持っていたと思いますが，この様な問題は真逆な，反面教師の典型ではないかということです．それで，見過ごしにできなかった訳ですが．

Re: 困っています…．

yama さんのレス (2006/12/03(Sun) 20:24)

問題が不自然だというのは，この問題のような状況はありそうもないということでしょうか？そういう見方もできるとは思いますが，単に運動量保存の理解をみる問題だと思えばこれでもいいと思います．分裂後の一方の物体が初速度に対してθの方向にvの速さで・・・としたほうが一般性があって不自然ではないと思いますが，具体的に数値計算をさせるという意味ではこの問題も意味はあると思います．

Re: 困っています…．

zoro さんのレス (2006/12/03(Sun) 21:48)

横から失礼します．細かな計算はさておき，大雑把な関係を描いて見ましょう．一応，2体運動での重心運動と相対運動を学ばれたとして書きます．

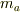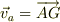最初に質点a,その質量は m_a で，速度 $\vec v_a =\overrightarrow{AG}$ で＋y軸の方向に進んでいたとします．

質点aが何らかの原因で，質点b,cに分裂し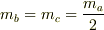， $m_b=m_c=\frac{m_a}{2}$ と等質量になった．

Gを分裂の瞬間の重心位置とし，分裂後に飛び出した相対運動量は，Gから見れば等しく，向きが逆ですね．

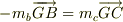
$-m_{b}\overrightarrow{GB} = m_{c}\overrightarrow{GC}$

この時に分裂質点に付与される相対エネルギは，分裂のメカニズムによって決まるので，大きさはなんともいえません．ただし，どんなメカニズムであろうと，分裂質点間による相互作用は常に作用反作用の法則に従うので，相対速度が大きさが等しく向きが逆になりますね．

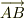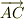上に書いた図を運動量と見直して，さらに外部からみた速度にするには， $\overrightarrow{AB}$ とか， $\overrightarrow{AC}$ を好みの方向や，大きさにすれば決められますね．

なお，質点aが直角方向に出るというのは，∠BAG＝直角を意味しますね．

【追伸】高校の問題としては，この手の運動量の保存が視覚的に出てくれば，あとは数学でとこまで表現するかになります．

本来は，「分裂の過程」にその反応の物理現象が隠されているのだと思います．言うならば，上の計算は物理現象が始まる初期状態(質点a)から反応を起こして終状態(質点b,c)に崩壊したばあい，質点bを直角位置で検出したときには，崩壊の相対方向と大きさがどれ程であったかを計算する基礎，これを運動学ともいったと思いますが，に馴染む為の例題と思います．

ですから，この計算は運動量の幾何学的特性を把握していれば十分と考えられますね．

Re: 困っています…．

なんとなくさんのレス (2006/12/03(Sun) 22:34)

了解しました．別にθに一般化しないでもいいですが，数値に（この問題はそう言う意味では計算が単純ですが）もう一工夫あっても良かった気がしますね．

Re: 困っています…．

zoro さんのレス (2006/12/04(Mon) 13:06)

前の説明は，運動量と速度の関係が不明瞭で，誤解を受ける可能性があるので，速度ベクトルの図により説明します．

＝＝＝＝＝＝問]速さ5.0m/sで飛んできた質量20kgの物体が質量10kgずつの二つの部分に分裂し，一方は分裂前と直行する方向に10m/sで飛んで行った．もう一方はどの向きにどれだけの速さで飛んでいくか．＝＝＝＝＝＝

この問題の味噌は；

・分裂前後での重心の運動量が保存し，・重心系が慣性系となり，重心からみた相対運動の運動量の総和がゼロ．

今回は，題意より相対速度が「逆向き」と制限されていることです．

<pre> 速度ベクトルの作図

C

・: ／／

／／／／

／／

・ G ／／｜／

／｜／／｜／／｜／

・・ B A </pre>

題意より

ある慣性系からみた重心の速度

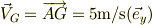
$\vec V_{G} =\overrightarrow{AG}= 5\mbox{m/s}( \vec e_{y})$

ある慣性系からみた質点bの速度

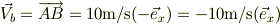
$\vec V_{b} = \overrightarrow{AB} = 10\mbox{m/s}(-\vec e_{x}) = -10\mbox{m/s}(\vec e_{x})$

重心から見た質点bの速度

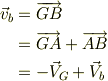
$\vec v_{b} &= \overrightarrow{GB} \\&= \overrightarrow{GA} + \overrightarrow{AB} \\&= -\vec V_{G} + \vec V_{b}$

重心系から見た質点cの相対速度は質点bと真反対だから

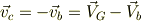
$\vec v_{c}=-\vec v_{b}=\vec V_{G} - \vec V_{b}$

もとの慣性系からみた質点cの速度は；

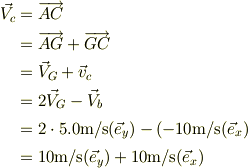
$\vec V_{c} &=\overrightarrow{AC} \\&= \overrightarrow{AG}+\overrightarrow{GC}\\&= \vec V_{G}+\vec v_{c}\\&= 2\vec V_{G} - \vec V_{b}\\&= 2\cdot 5.0\mbox{m/s}( \vec e_{y}) - (-10\mbox{m/s}(\vec e_{x})\\&= 10\mbox{m/s} (\vec e_{y}) +10\mbox{m/s}(\vec e_{x})$

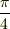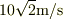と，質点bとは逆サイドで+y軸から $\frac{\pi}{4}$ 方向に, $10\sqrt{2}\mbox{m/s}$ の速さで進行する．

＝＝＝＝検算

其々の質点の速度から全体の運動量を出してみる．

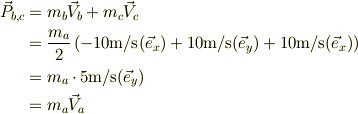
$\vec P_{b,c} &= m_{b}\vec V_{b} + m_{c}\vec V_{c} \\&= \frac{m_{a}}{2}\left( -10\mbox{m/s}(\vec e_{x}) + 10\mbox{m/s} (\vec e_{y}) +10\mbox{m/s}(\vec e_{x}) \right) \\&= m_{a}\cdot 5\mbox{m/s}( \vec e_{y} ) \\&= m_{a}\vec V_{a}$

と，分裂の前後の運動量は保存している．

Re: 困っています…．

トンガリさんのレス (2006/12/04(Mon) 16:34)

速度には方向があるので，速度はベクトル和で考えるのが常識です．運動量にも方向があるので，運動量もベクトル和で考えるべきです．運動量保存で私は時々これを忘れますが・・・この[問]は初速度で移動する座標系で見て重心不動で考えるのも明解ですが，私はベクトル和に固執して考えます．図が使えないので，分かりにくい表現になりますが，

例に，速さ5m/sで質量10kgの鋼球がY-からとY+からと飛んできて正面衝突時のベクトル和を試みます． Y-から飛んできた鋼球の衝突前の運動量＝50Kgm/S，衝突後の運動量＝-50Kgm/Sで正しいでしょう．この衝突後の運動量は衝突前の運動量50Kmg/S−衝撃100Kmg/S＝-50Kg/Sで計算されたとします．ところで，衝撃100Kg/Sは何処から来たのか．ベクトル和で計算が合うだけのベクトルだ．それでも，反作用で， Y+から飛んできた鋼球の衝突後の運動量＝衝突前の運動量-50Kgm/S＋衝撃100Kmg/S＝50Kgm/Sを得ます．これと同様に，運動量の保存だかベクトル和で計算が合うだけの衝撃ベクトルを使って[問]を解かんとします．

[問]を，速さ5.0m/sで飛んできた質量10kgずつの二つの物体Ａ,Ｂとします．物体Ａは，右前方Atan(100／50)＝63.435度の方向から，衝撃√(100^2＋50^2)＝223.61Kmg/Sを受けると，物体Ａはベクトル和でAtan[-100／(50−50)]＝-90度の方向に運動量√[100^2＋(50−50)^2]＝100Kmg/S で飛ばされる．すなわち，【問題】物体Ａは左真横に10m/sで飛ばされる．

物体Ｂは，爆発による反作用で，左後方63.435度の方向から，衝撃223.61Kmg/Sを受けるので，物体Ｂはベクトル和でAtan[100／(50＋50)]＝45度の方向に運動量√[100^2＋(50＋50)^2]＝100√2Kmg/S で飛ばされる．すなわち，【答え】物体Ｂは右前方45度の方向に10√2m/sで飛ばされる．

私は爆発の方向と大きさを示す衝撃ベクトルを導入しましたが，正しかったでしょうか．爆発の途中経過が無用なら，爆発を無視できるなら，ｙａｍａさんの No.13008 の反作用が最も明解です．爆発前後で運動エネルギーは増加しますが運動量は保存されます．運動量保存では爆発を無視できる理由は，爆発で物体に作用する衝撃が作用反作用の法則で衝撃のベクトル和がゼロとなるからです．衝突にしろ爆発にしろ，物体に働く衝撃のベクトル和は作用反作用の法則でゼロとなる．これは3個以上の物体での爆発でも成り立ちます．言い換えれば爆発では重心不動で物体が飛び散ります．ただし，ここでの爆発では各々の物体は回転しないで飛び出すことを前提としています．

[home] [掲示板] [ページの先頭]