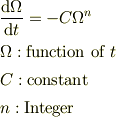微分方程式の解

微分方程式の解

z さんの書込 (2006/11/30(Thu) 20:38)

以下の微分方程式をtについて解きたいです．ご教授お願いいたします．

&\frac{\mathrm{d}\Omega}{\mathrm{d}t}=-C\Omega^n \\&\Omega:\text{function of }t \\&C:\text{constant} \\&n:\text{Integer}

答えは

> ! Extra }, or forgotten \right.

のようなんですがなぜこうなるんでしょうか

Re: 微分方程式の解

twister さんのレス (2006/11/30(Thu) 22:13)

始めまして．

答えが見にくいですが，少なくとも，n=1 については，別途考察する必要がありますね．

解らないところをもう少し詳しく書けますか？

逆に質問ですが，変数分離といった手法を聞いたことがありますか？

Re: 微分方程式の解

z さんのレス (2006/12/01(Fri) 02:36)

ヒントをありがとうございます． >逆に質問ですが，変数分離といった手法を聞いたことがありますか？ あります．私の問題の場合はn≠1です． 変数分離とは

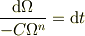
\frac{\mathrm{d}\Omega}{-C\Omega^n}=\mathrm{d}t

にするということでしょうか

Re: 微分方程式の解

サボテン さんのレス (2006/12/01(Fri) 07:18)

横から失礼致します． あとは両辺積分するだけです．

Ω^(-n+1)/[C(n-1)]=t+D (Dは積分定数) となります．

あとは初期条件からDを決めればよいのではないでしょうか?

Re: 微分方程式の解

twister さんのレス (2006/12/01(Fri) 08:46)

zさん：

サボテンさんの仰る通りで，両辺別々に積分できるところが味噌ですね．自分も，この手法を知ったときは狂喜乱舞した記憶があります．

私は，この方法には2つの味噌があると思います．厳密性に欠けているでしょうが，自分のフィーリングを書いてみます．

1) 独立変数の微分 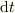\mathrm{d} t を辺々に掛ける． この手法こそ，微分方程式を自在に変形する有効な手法の一つですよね．

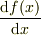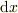これに限らす，ある任意の微分の式， \frac{\mathrm{d} f(x)}{\mathrm{d} x} に， 微分 \mathrm{d} x を掛けてしまえば，新たな微分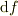， \mathrm{d} f が生まれる．

2) tの関数である 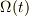\Omega(t) とtだけの式に変形する． これこそが変数分離なわけですね．

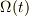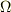その結果，tの従属変数(関数)であった， \Omega(t) が， あたかも独立変数 \Omega として振舞う事が凄いのだと思います．

＝＝＝＝＝

物理の中の式には，古典力学から量子力学まで，色々な場面で，形をかえてこの変数分離が出てきますね．デモ，変数分離を見つけたら，もうこっちの勝利ですね(笑)．

Re: 微分方程式の解

twister さんのレス (2006/12/01(Fri) 10:22)

zさん：

変数分離もご存知ということは，「最終解が示された解にならない」ということでしょうか？

お書きになっている

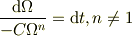
\frac{\mathrm{d}\Omega}{-C\Omega^n}=\mathrm{d}t, n \ne 1

を左右積分すれば，サボテンさんの書かれた様に；

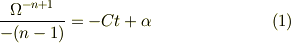
\frac{\Omega^{-n+1}}{-(n-1)} = -Ct + \alpha \tag{1}

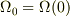ここで，初期条件； t=0 で \Omega_0 = \Omega(0) とすれば，

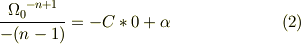
\frac{{\Omega_{0}}^{-n+1}}{-(n-1)} = -C*0 + \alpha \tag{2}

式(1),(2)を辺々引いて，整理すれば

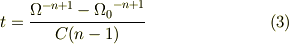
t= \frac{\Omega^{-n+1}-{\Omega_{0}}^{-n+1}}{C(n-1)} \tag{3}

分子については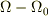， \Omega - \Omega_{0} で括れるとも思いますが，物理の問題ならそこまで変形する必要はないと思います．

Re: 微分方程式の解

z さんのレス (2006/12/01(Fri) 11:10)

ありがとうございました．大変参考になりました．