測定誤差の式

測定誤差の式

ku さんの書込 (2006/11/26(Sun) 23:22)

光電比色計を用いた吸光度測定に関する問題です． T=eのときに誤差が最小になるようなのですが，以下の式の求め方がわかりません． よろしくお願い致します．

Beerの法則が成立する溶液においては濃度の相対誤差?C/Cは?A/A（Aは吸光度）に等しく 次の関係が示される．

?C/C=log(e)・?T/Tlog(T)=?T/Tln(T)

ここでTは透過率の誤差である．A=-log(T)の関係からこの式を導け．

Re: 測定誤差の式

twister さんのレス (2006/11/27(Mon) 01:05)

始めまして．

理化学辞典で，光の吸収に付いてのランバート-ベールの法則(Lambert-Beer's low)をみると，

入射光の強度 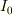I_0 ，透過光の強度 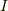I ，吸収物質の厚さx，濃度をC，比例係数kとすると；

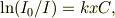
\ln(I_0/I) = kxC,

と在ります．透過率, 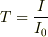T = \frac{I}{I_0} でしょうから，

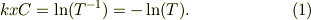
kxC = \ln(T^{-1}) = -\ln(T). \tag{1}

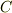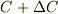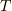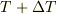濃度 C が濃度 C+\Delta C に変化するとき，透過率 T が透過率 T+\Delta T に変化するとすれば，両者の関係は上式の微分を取れば定まるので，

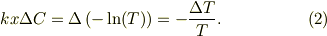
kx\Delta C = \Delta\left(-\ln(T)\right) = -\frac{\Delta T}{T} \tag{2}.

式(2)と式(1)とで辺々の比を取ると，

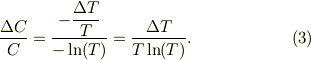
\frac{\Delta C}{C} =\frac{ -\dfrac{\Delta T}{T}}{-\ln(T)}= \frac{\Delta T}{T\ln(T)}.\tag{3}

どちらかというと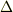， \Delta を誤差と考えるより，変化分と考える方がイメージし易いと思います．

なお，定義から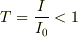， T = \frac{I}{I_0} < 1 では無いでしょうか．

しかし，式(3)から濃度の微分式；

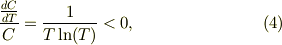
\frac{\frac{d C}{d T}}{C} = \frac{1}{T\ln(T)} < 0, \tag{4}

を考えて，この絶対値が最小になる，言い換えれば感度が最小な条件をだすと考えれば，上式をTで微分し，それがゼロの条件を探せば良いと思います．あとはご自分で求められますね．

Re: 測定誤差の式

なんとなく さんのレス (2006/11/27(Mon) 01:26)

はじめまして，kuさん． 何となくと言います． ちょっと目に付いたので，Beerの法則なるものは知りませんが，この問題は純粋に数学的にできそうです． A=-log(T)より，ΔA=Δ(-log(T))=-ΔT(1/T)/ln(10) したがって， ΔA/A=-ΔT(1/T)/ln(10)・(-log(T))=ΔT/Tln(T) となります． 要するに，次の２点に注意すればいいです． (1) Δを作用させる式は微分作用素と同じ式で表される．したがって Δ(log(T))〜d(log(T))/dx=dT/dx(1/T)/ln(10) と考えれば，Δ(log(T))=ΔT(1/T)/ln(10) (2) logは底10なので，底をeに変換すると,log(T)=ln(T)/ln(10)

以上．

Re: 測定誤差の式

ku さんのレス (2006/11/27(Mon) 02:07)

twisterさん，なんとなくさんありがとうございます． 大変参考になりました．また質問させていただくかもしれませんがよろしくお願いしますm(＿＿)m