フーリエ級数

フーリエ級数

R. C. さんの書込 (2006/11/10(Fri) 08:03)

こんにちは． 私は生物系の大学生で，大学レベルの物理/数学は線形代数を半年習っただけなのですが， 興味はあるので，独学でいろいろ勉強しております．

さて，(複素)フーリエ級数の式，

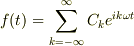
f(t) = \sum^{\infty}_{k=-\infty}C_k e^{ik\omega t}

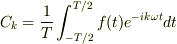
C_k = \frac{1}{T} \int^{T/2}_{-T/2}f(t)e^{-ik\omega t} dt

についてです．

よく教科書には，上の式を下の式に代入して，確かに係数が一致することを， 直交性に基づいて説明してあります． しかし，下の式を上の式の右辺に代入しても，ちゃんとf(t)が出てくるはずです． そう思って，代入してみたのですが，

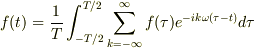
f(t) = \frac{1}{T}\int^{T/2}_{-T/2}\sum^{\infty}_{k=-\infty}f(\tau)e^{-ik\omega(\tau-t)}d\tau

という積分が出てきて，詰まっております． 何分，演習経験が少ないので，計算力がないのだと思いますが，アドバイスをくだされば幸いです．

Re: フーリエ級数

twister さんのレス (2006/11/10(Fri) 11:10)

はじめまして．

きっと誰でも，一度はやったことが有ると思います．

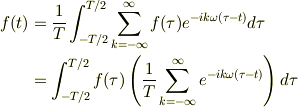
f(t) &= \frac{1}{T}\int^{T/2}_{-T/2}\sum^{\infty}_{k=-\infty}f(\tau)e^{-ik\omega(\tau-t)}d\tau \\&=\int^{T/2}_{-T/2}f(\tau)\left( \frac{1}{T}\sum^{\infty}_{k=-\infty}e^{-ik\omega(\tau-t)}\right) d\tau

ですから，荒っぽく言えば，デルタ関数を再発見していたのだろうと思います．

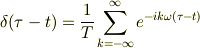
\delta(\tau-t) = \frac{1}{T}\sum^{\infty}_{k=-\infty}e^{-ik\omega(\tau-t)}

こういう事を書くと，数学系の面々が渋い顔をされていると思いますが...． ;P

[追記]なにかファクタ 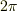2\pi がどっかに入りませんでしたっけ？

Re: フーリエ級数

toorisugari no Hiro さんのレス (2006/11/10(Fri) 20:52)

>

> [追記]なにかファクタ 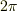2\pi がどっかに入りませんでしたっけ？

これでいいですよ．

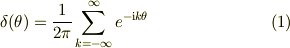
\delta(\theta) = \frac{1}{2\pi}\sum^{\infty}_{k=-\infty}e^{-\mathrm{i}k\theta} \tag{1}

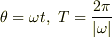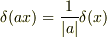を認めれば， \theta=\omega t,~ T=\frac{2\pi}{|\omega|} と \delta(a x)=\frac{1}{|a|}\delta(x) から上の式がでますね．

(1)が成り立つかは．．．．「証明」は結構やっかいだったはず．

Re: フーリエ級数

twister さんのレス (2006/11/10(Fri) 22:08)

toorisugari no Hiroさん：

>これでいいですよ． >(1)が成り立つかは．．．．「証明」は結構やっかいだったはず．

ご助言，有難うございます．書いてからすぐ外出してしまい，冷や汗をかいていました．

  1. C.さん，自分の指と目で計算するのは，地力が付くと思うので，疑問が出てきたら質問するのが賢い選択だと思います．

生物系もワトソンさんからほぼ半世紀たち，精密科学の様相が日増しに強まっている中，数学や物理も生物の良きツールとして使い倒してくださいね．

Re: フーリエ級数

R. C. さんのレス (2006/11/10(Fri) 22:48)

こんばんは．

複素解析学の結果を使ったら出てくるのではないかと疑っていたのですが， デルタ関数が絡んでくるとなると，厳密な証明は難しそうです． とりあえず，(1)は形式的な証明を受け入れておくことにします． (正規分布のフーリエ展開の極限を取るやつです)

ありがとうございました．

>自分の指と目で計算するのは，地力が付くと思うので

生物学というのは，博物学が先祖ですから，論理的な体系をつくって演繹するよりは， 「面白いことを探して，あとから理屈を考える」側面が強いです．

そういう土壌にいるので，数学も，始めのうちは，面白そうな結論や応用面ばかりに 目が行って，感覚的な説明で済ませていたのですが，最近は証明や論理の流れ(何か ら何が出てくるか)にも興味が湧くようになり，実際に手を動かしていじったりしています．

今後ともよろしくお願いします．