エネルギー保存則
エネルギー保存則
ちょめ さんの書込 (2006/11/06(Mon) 20:07)
こんばんは.理系で今,浪人をしています.力学は一通り学習しています.
名門の森(力学・波動)[著:浜島清利][河合出版]という問題集の,P36の12の問題に関してなのですが,以下に問題文・設問を書きます.
長さ6aの糸の両端と中央に,同じ質量mの小さいおもりA,B,Cを付け,水平線上に固定された滑らかなくぎP,Qに掛けた.PQ=2aであり,重力加速度をgとする. (わかりづらいと思いますが,糸がM字型のようになっている状況です) 問1:3つのおもりがつりあって静止している.Bは水平線PQよりどれだけさがっているか. 2:Bを手でつまんでPQの中点まで持ち上げる.このとき手のした仕事を求めよ.
答えは1はa/√3,2は(2-√3)mgaです.1は問題ないので2について質問をさせて頂きます. 解答では,手の仕事=位置エネルギーの変化として答えを出しているのですが, この時,張力による仕事はどうなっているのでしょうか?明らかに仕事をしていると思うのですが・・・ また,ちゃんと式をたてて答えを出そうとしたのですが,こちらも答えと合いませんでした. 「まず,静止状態のBの位置を原点とし,上を正とする座標をとる.問題文には書いていないのですが,加速度0,つまり等速で持ち上げたとして,また,Bについている糸と座標軸がなす角をθとし,手が及ぼす力をF,張力をTとしてBについての運動方程式をたてると, 0=F+2Tcosθ-mg・・・? 問1よりPQの中点と静止しているときのBとの距離はa/√3であり,時刻tにおけるBとPQの中点とPを頂点とする三角形で三平方の定理を用いると,時刻tにおけるBとPの距離は√(a^2+((a/√3)-x)^2)となるから, cosθ=(a/√3)-x)/{√(a^2+((a/√3)-x)^2)} これを?に代入し,両辺にエックスドットをかけて整理すると, 0=d/dt(Fx-2T{√(a^2+((a/√3)-x)^2)}-mgx) したがってこれをt=0〜PQの中点に達する時刻まで積分して, 0=F(a/√3)-2Ta-mg(a/√3) 問1でT=mgがわかるので 手のした仕事=F(a/√3)=2Ta+mg(a/√3)=2mga+mg(a/√3)=(2+(1/√3))mga」 となり,答えと違ってしまいます.
絵がないのでわかりづらいかとは思いますが,お答えいただければと思います. よろしくお願いいたします.
Re: エネルギー保存則
yama さんのレス (2006/11/06(Mon) 22:43)
ちょめさん,こんばんは. ヒントになりそうなことを書いておきますから,あとは考えてみてください.
張力はそれぞれのおもりに対しては仕事をします. しかし,3つのおもりにする仕事を合計すると 0 になります.つまり張力全体としては仕事をしないわけです. このことはそれぞれの糸の両端のおもりにはたらく張力の大きさが等しいことと,糸が伸び縮みしないことから導くことができます.
次に,あなたの解では B を等速で持ち上げるとしていますが,この場合,A と C の運動は等速運動ではなく,加速度運動になるので,T=mg は成り立ちません.
Re: エネルギー保存則
ちょめ さんのレス (2006/11/07(Tue) 11:55)
お返事ありがとうございます.
>しかし,3つのおもりにする仕事を合計すると 0 になります. なるほどそういうことだったんですね. >このことはそれぞれの糸の両端のおもりにはたらく張力の大きさが等しいことと,糸が伸び縮みしないことから導くことができます. とありますが,一度数式で確認しておかないとなんだかもやもやするのですが・・・大学受験者には瑣末なことなんでしょうか・・・
それと, >A と C の運動は等速運動ではなく,加速度運動になるので,T=mg は成り立ちません. とありますが,Bを等速とした場合,A,Cは逆向き同じ大きさの速さで等速になり,T=mgとなると思うのですが,違いましたでしょうか?
質問ばかりですみません.
Re: エネルギー保存則
なんとなく さんのレス (2006/11/07(Tue) 14:18)
横レス,失礼します. ちょめさん,こんにちは.なんとなくです. 最初の質問で運動を考えておられますが,時間の概念を入れないほうが良いと思います.非常にゆっくりと持ち上げることを考えれば(大学では準静的とか言いますが,要は瞬間的に釣り合っている状態を連続させるということです),各瞬間に釣り合いの式(ちょめさんの立てられた式で合っていると思います)から力f(x)を決定し,∫f(x)dxで所定の結果が得られると思います.高校では保存力は習っていましたっけ?この問題のポテンシャルは重力によるもので,エネルギーの変化はその経路によりません.つまり,どのような動作(速度)で持ち上げようとも結果が同じことは保障されていると言えます. あと,勝手に答えると,静止状態から等速運動を仮定しても加速(度領域)無しでは移れません.上記の準静的はその辺をうまくごにゃごにゃ・・・(軽いオヤジでどうもすみません).
Re: エネルギー保存則
ちょめ さんのレス (2006/11/07(Tue) 16:53)
なんとなくさん,こんにちは.お返事ありがとうございます. 確かに,∫f(x)dxを計算することにより解答と同じものが得られました!! T=mgとして計算しましたので,時間で積分したときに間違った値が出てきたのは計算ミスだったんでしょうか?・・
保存力は,ある力Fが保存力のとき,A点からB点までFがする仕事は経路によらないと習いました.
>静止状態から等速運動を仮定しても加速(度領域)無しでは移れません. x=0で急に速度vにし,x=a/√3で急に速度0にする場合,加速度が常に0の等速運動とはみなせないのでしょうか?
Re: エネルギー保存則
yama さんのレス (2006/11/07(Tue) 17:42)
B が上向きに dx だけ無限小変位したとして,そのときに張力がA,B,Cにした仕事を計算すると合計で 0 になることが分かります.
B が上昇すると,BP の長さが減少していきますが,B の上昇速度が一定でも BP の長さの減少速度は一定ではありません.そのため A が降下する速度も一定ではなくなります.特に B が PQ の中点に近づくと A の降下速度は 0 に近づきます.C の速度についても同様です. 従ってAとCの運動エネルギーも変化するので,それに伴う仕事を考える必要があります.また,初期加速の取扱いも問題です. このような面倒なことを避けるには,なんとなくさんの言われるように,各瞬間に釣り合いを保ちながらゆっくりと上昇する場合を考えるのがいいと思います.その場合は当然釣り合いの式 T=mg が成り立ちます.
>T=mgとして計算しましたので,時間で積分したときに間違った値が出てきたのは計算ミスだったんでしょうか?・・
等速度のときは T=mg が成り立たないのでもちろん間違いですが,正しい力の式を用いても単純に時間で積分しただけでは求める仕事にはなりません.運動エネルギーの変化と初期加速が考慮されていないからです.
>x=0で急に速度vにし,x=a/√3で急に速度0にする場合,加速度が常に0の等速運動とはみなせないのでしょうか?
みなせません.速度が急に変化するときは非常に大きい加速度が生じます. またこの問題の場合,Bを瞬間的に速さvまで加速するときの仕事と,終点で急に0に減速するときの仕事の絶対値は等しくありません.なぜなら終点近くではAとCの速さはほとんど0になっているからです.
Re: エネルギー保存則
なんとなく さんのレス (2006/11/07(Tue) 18:09)
ちょめさん,私からは何にも付け加えることはありません.それどころか,またyamaさんに考え方を教えてもらいました.なるほど加速時と減速時の違い,ふむふむ勉強になるなあ.あー,ひとつだけ,式にこだわるのなら,エックスドットを掛けたあと,d/dtを抜き出す際に,F,Tを定数とみなして扱っているようですが,これらは位置の関数であり,当然時間の関数ですので簡単に外せません,と思いますよ.
Re: エネルギー保存則
ちょめ さんのレス (2006/11/07(Tue) 18:44)
丁寧なお返事ありがとうございます. とても納得がいきました! 確かに,yamaさんがおっしゃるとおりBが等速でもA,Cは等速でないのでF,Tは時間(位置)の関数でしたね><
質問できる人が身近にいないので,本当にありがたいです. わからないところがたまっていたので,また質問させていただくと思いますがよろしくお願いしたいと思います. どうもありがとうございました!
Re: エネルギー保存則
yama さんのレス (2006/11/07(Tue) 22:49)
ちょっと説明に不備があったので補足しておきます. Bを瞬間的に加速しても糸がたるんでしまうので,AとC が降下する加速度は重力加速度を超えることはありません. しかし,糸のたるみを考慮するのはかなり面倒なことになりそうです.
Re: エネルギー保存則
twister さんのレス (2006/11/08(Wed) 09:27)
横から失礼します.
yamaさん:
「糸」の条件は, 1) 引っ張る事はできても,押すことは出来ない. 2) 長さは伸びない. 3) 質量はない. だけでないでしょうか.
指が加える力が強すぎて中央の重りの速度が早くなれば,左右の重りは自由落下して速度をゲインしますが,途中から指の力が減少したり,逆方向(下方に)に力を加えたりして,終状態の速度をゼロにするだけで良いのではないでしょうか.
原理的には,指で重力加速度を越える加速をしてもいいし,その逆に重力加速度を越える減速も許されてしかるべきだと思いますが....
もちろん,「糸がたるまない」という条件があれば,張力をいれた運動方程式が解釈し易いと言う点では賛成です.しかし,この条件以上に,準静的な加速を要請する必要はないように思います.
Re: エネルギー保存則
yama さんのレス (2006/11/08(Wed) 10:22)
もちろん,それでいいわけで,結局は位置エネルギーの変化を求めればいいわけです. しかし,位置エネルギーの変化によらないで,手の力を用いて直接仕事を計算する場合は,速度が0でなければ計算がかなり面倒になります. 準静的な加速を要請するのは,単に計算を簡単にするためです.
Re: エネルギー保存則
twister さんのレス (2006/11/08(Wed) 12:00)
>もちろん,それでいいわけで,結局は位置エネルギーの変化を求めればいいわけです.
という意味では,この問題を拝見した時から,なぜそうして解かないか不思議でした.
しかし,出題者さんは,連立運動方程式と糸の束縛条件を入れて解き,かつ外力の仕事を計算すると,エネルギー保存則がでる,言い換えれば「エネルギーの保存則」を回答者に再体験させたかったのではなかろうかと思いました.
そのように考えると,運動エネルギーの項を自分で計算に入れるというのは,よい経験と思います.計算を簡単にするために加速度の項の積分を無視するのは,教育的な観点に沿わないと思います.
むしろ,「運動方程式の取り扱いが,いかにも微妙なテクニックに支配される」と誤解される危険性がある,と感じました.
Re: エネルギー保存則
yama さんのレス (2006/11/08(Wed) 12:40)
質問者のちょめさんによると,問題集の解答では「手の仕事=位置エネルギーの変化として答えを出している」ということなので,出題者は運動方程式からエネルギー保存則を導かせることを意図したわけではないでしょう. 質問者が「手の仕事=位置エネルギー」とすることに疑問をもち,等速運動を仮定して直接手の仕事を計算してみたものの解答と合わないので,この掲示板に質問されたのだと思います. 大学生なら一般的な場合を運動方程式に基づいて考察するのは教育的だと思いますが,質問者は浪人生なので,そこまでは必要ないように思います.
Re: エネルギー保存則
twister さんのレス (2006/11/08(Wed) 13:04)
なるほど,受験問題であることを忘れていました.
すると,現在の高校では,運動エネルギーをどのように説明するのでしょうかね?
ひょっとして,高校生が;
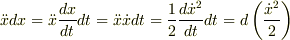
この関係を使ってはいけないとか?
Re: エネルギー保存則
yama さんのレス (2006/11/08(Wed) 16:29)
高校物理の教科書では,基本的には微積分は使用されていません.
数学で微積分を含む科目が必修ではない上,物理の履修が数学で微積分を学ぶ前になることもあるので,微積分の知識を前提とすることはできないからです.
運動エネルギーも当然微積分を用いずに説明されます.
速さvで動いている質量mの物体が別の物体に一定の力Fを加えて動かし,反作用を受けて等加速度で減速して停止するまでに物体にする仕事を等加速度運動の公式を用いて求めると 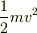 になることを導いて,これが運動エネルギーであると説明するわけです.
当然,等加速度でない場合はどうなのかという疑問が出てきそうですが,それについてはきちんとした説明をしないまま,先に進むことが多いようです.
になることを導いて,これが運動エネルギーであると説明するわけです.
当然,等加速度でない場合はどうなのかという疑問が出てきそうですが,それについてはきちんとした説明をしないまま,先に進むことが多いようです.
しかし,微積分を用いることが禁止されているわけではないので,数学の履修状況によっては授業で微積分を用いて説明することもあると思います.
Re: エネルギー保存則
twister さんのレス (2006/11/08(Wed) 19:40)
ちょめさん,横から口出しして済みませんでした.
運動方程式が微分方程式で与えられ,重力の元の運動はエネルギ保存則まで説明をされているものとして眺めていました.
そうと判れば,ちょめさんの疑問は真に良い疑問だと思います.絵を描くのが巧くないので,少し時間がかかりますが,連立微分方程式と束縛条件から運動エネルギと位置のエネルギで表すようにして見ます.連立方程式から張力が消去され,束縛条件から3つの重りのエネルギを分離できることを示せると思います.
yamaさん,ご丁寧な解説有難うございました.
基本的には微積分は物理で使えないことを理解しました.でも,この掲示版は,文科省の認可を受けているわけでもないわけです.中学生だろうが,高校生だろうが,もし無理なく微積分や複素数・複素関数,線形代数を使えるなら,それを使って物理を勉強,というより探索しても良いのではないかと思うこのごろです.
小学生の頃,「鶴亀算」というのが判りにくかったのですが,中学で変数が入って,感激しました.これと同じで,便利な道具があり,それを使う目的が明確であるなら,ドンドンつかって概念を広げるのが重要では無いかと考えます.落ちこぼれのひがみでしょうかね.
Re: エネルギー保存則
ちょめ さんのレス (2006/11/08(Wed) 20:44)
>ちょめさん,横から口出しして済みませんでした
いえ,他の人のためにもなったようでよかったです^^
自分は高校のとき,ちょっと勉強が出来ない状態にありましたので,物理も浪人してから予備校でほとんどゼロから習い始めました.学校や多くの予備校では微積分などは使わないで教えるのだと思いますが,自分のところの先生は公式といわれてるようなものを微積や内積,外積などをつかって導いて教えてくれました.
ですので,多くの高校生は手の仕事=位置エネルギーの変化とすぐ出来るのでしょうが,自分は運動方程式を書いてから式を眺めてそこからエネルギー保存などを導かないと不安な感じです.(試験ではxドットをかけて・・とやってる時間はなさそうなので,式まで書かなくとも手の仕事=位置エネルギーの変化のような関係がすぐにわからないといけないのですが・・・^^;)
Re: エネルギー保存則
twister さんのレス (2006/11/08(Wed) 22:09)
ちょめさん:
>自分のところの先生は公式といわれてるようなものを微積や内積,外積などをつかって導いて教えてくれました.
そこまで徹底してするのも一手と思います.この場合の注意は,物理的な解釈をおろそかにして,計算に流される事ですね.そういう意味で,教える側がセンスを磨かねばいけないのだろうと思います.
>多くの高校生は手の仕事=位置エネルギーの変化とすぐ出来るのでしょうが
これは,これで,答えは出るものの,解釈のしようがないという問題ですね.私としては,このような形式的な方法で物理を学んで欲しくないと思います.
>自分は運動方程式を書いてから式を眺めてそこからエネルギー保存などを導かないと不安な感じです.
ここらをどうして対応するかが,高校生さんや高卒生さんを教えるときの課題なんでしょうね.
ですから,具体的な数例に付いて,丁寧に解いた例をじっくりと観察して,その結果を整理して覚えると良いと思います.例えば,今回の例で言えば,位置エネルギだけが導入されても,保存則に到達しないので,理解するきっかけが無いのだと思います.
やはり,『「運動エネルギ」+「位置エネルギ」= 一定:全エネルギの保存』まで行かないと問題を解釈できないのだろうと思います.
なんのかんの書きましたが,初めて学ぶ領域について,自分なりの疑問を持てるということは,とても素晴らしいことと思います.初心者の時に「どれだけ自分の目で疑問を見出すか」というのは大事だろうと思います.
Re: エネルギー保存則
twister さんのレス (2006/11/11(Sat) 23:04)
ちょめさん:
こういう特殊な例題を丁寧に解く意味がどれだけあるか判りません.しかし,複雑な系でも,重力しか関与しない場合,外力がする仕事は,系の運動エネルギと位置エネルギに転換するということを示してみました.
ふつう,この手の積分は,単純なバネの系などで示されると思いますが,複雑系でも同じな事を味わってください.
以後,重力とかバネとかの保存力系では,他の外力が無い限り,「運動エネルギと位置エネルギの総和は保存する」ことを気楽に使えるでしょう.
<pre> <図> B の位置 x: 原点はO,上方に向かって正とする. ● / ↑ θ≡∠QBO, / f(t) tan(θ)=a/x, x=a/tan(θ); sin(θ)=a/z, z=a/sin(θ) (y) / z≡|BQ|=sqrt(|OB|^2 + |OQ|^2)=sqrt(x^2 + a^2) ↑ / \ a<=z<=3a / \ P / O \ Q |PQ| = |OP| = a ◎ + ◎ | | | | | | | | |QC|=3a - z | | ∴ 0 <= |QC| <= 2a | | | | | | | |↑T:張力 | | A ● ● C
C の位置 y= -(3a - z) 原点はQ,上方に向かって正とする. </pre>
<運動方程式>
Bの運動は,
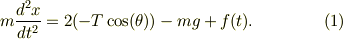
A,Cの運動は,
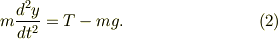
糸の条件



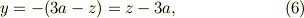


静止の場合,式(1),(2)で加速度と外力がゼロだから;
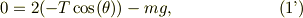

上記の静止解には下付き添え字zeroを付けて表すと;

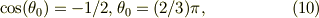
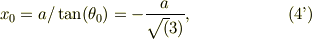
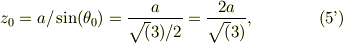
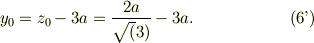
運動方程式(1)で,式(2)より張力 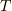 を消去すると;
を消去すると;
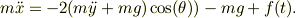
式(3)を用い,指の力 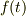 について整理すれば;
について整理すれば;
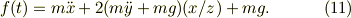
式(6)より,
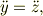
に注意すると,式(11)は,(x,z)だけの関数となる;
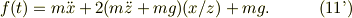
従って,静止状態からBに力を加えて,  が時刻
が時刻 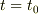 に
に 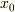 あったのが,時刻
あったのが,時刻 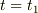 に
に 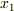 移動し,同時にA,Cが糸を通じて,
移動し,同時にA,Cが糸を通じて,  も
も 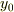 から
から 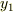 に移動するとき,指がBにする仕事,
に移動するとき,指がBにする仕事, 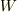 は;
は;
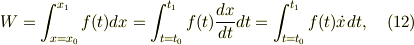
として計算できる.いわゆる仕事の積分である.
式(11')の各項目ごとに,式(12)の積分形式から都合のよいものを選択すればよい.なお,zは糸をとうして束縛されている;式(4)〜(7)を考慮する必要がある.式(7)の時間微分を取ると;
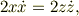
よって,

これを式(11')に適用すれば,
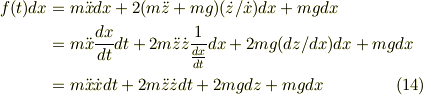
ここで,任意の時間の関数g(t)に対して,
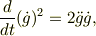
または

だから,式(14)は全て全微分の形に整理できる;
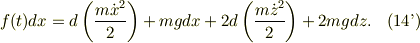
故に,指がBにする仕事, 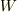 は;
は;
![W &=\int_{x=x_0}^{x_1}f(t)dx \\&= \left[\frac{m\dot x(t)^2}{2}\right]_{t=t_{0}}^{t_1} +[mgx]_{x_0}^{x_1} +2\left[\frac{m\dot z(t)^2}{2}\right]_{t=t_{0}}^{t_1} +2[mgz]_{z_0}^{z_1} \\&= \left[\frac{m\dot x(t)^2}{2}\right]_{t=t_{0}}^{t_1} +[mgx]_{x_0}^{x_1} +2\left[\frac{m\dot y(t)^2}{2}\right]_{t=t_{0}}^{t_1} +2[mgy]_{y_0}^{y_1}. \tag{16}](http://hooktail.maxwell.jp/bbslog/da6cbb84d2fd496987d4427ecbb693c1.png)
ここで,右辺の第1項は「Bの運動エネルギ」,第2項はBの位置エネルギを表します.同様に第3項は「AとCの運動エネルギ」,第4こうは「AとCの位置エネルギ」を表します.
このように考えれば,外力に付いての仕事積分は,運動エネルギと位置エネルギとに転化されていることがわかります.逆に,外力が無ければ,初期条件から運動方程式に従った運動が起きるものの,エネルギ保存をしていることがわかります.
また,大切なのは,仕事積分は,運動の詳細が判らなくても解けてしまうことです.その為に,「準静的な力」といった難しい論議はいらない事になります.でも,式(8)のような条件があることは念頭においておいてください.
注意しなければならないのは,「摩擦力」のように非可逆的な作用があるばあいは,エネルギ保存が成立しないことです.
最後になりますが,以上の結果,与えられた系で,静止状態(運動ゼロ)から指である変位まで動かして止めた場合,系は位置エネルギだけ変化することがわかりますね.
以上.