波動関数について・・・.
波動関数について・・・.
ドンマイ星人 さんの書込 (2006/11/05(Sun) 13:49)
こんにちわ.演習問題にこのような問題がありました.
「時間によらない波動関数の1回微分は,V(x)が有限のとびを持つところであっても連続である事を示せ.」
・・・この問題,連続である事は確かにイメージ付くのですが,果たしてどのように証明するか,その方法がわかりません. 2回微分して,定数(実数?)になればいいのかな・・・なんだかよく分かりません. どなたか,智恵をお貸しくださいませ<(_ _)>
Re: 波動関数について・・・.
のぼりん さんのレス (2006/11/06(Mon) 02:50)
こんばんは.眠れなくて起き出して仕舞いました.門外漢の戯言ですので,頓珍漢かも知れません.その節はご容赦下さい.
「V(x)」ということは,一次元の時間によらない波動方程式 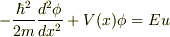 ですね?
ですね? 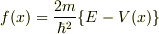 とおけば,f(x) は高々可算個の離散点を除き性質の良い(たとえばリプシッツ連続な)関数で,方程式は,
とおけば,f(x) は高々可算個の離散点を除き性質の良い(たとえばリプシッツ連続な)関数で,方程式は,
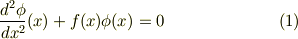
になります.この離散点を …,a −2 ,a −1 ,a 0 ,a 1 ,a 2 ,… だとします.前提より,各 a k における f の跳びは有限です.従って, 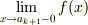 が存在します.開区間 (a k ,a k+1 ) において,f をa k+1 から ε だけ右側に連続になる様に適当に延長し,これを f’ として,(a k ,a k+1 +ε) で性質が良いとします.この f’ に対し,(a k ,a k+1 +ε) において,初期条件 φ(a k+1 )=c を満たす (1) の一般解が一意に存在します.これを u(x,c) と書きます.同様に,(a k+1 −ε,a k+2 ) で,左側に延長した f に対し,初期条件 φ(a k+1 )=c を満たす (1) の一般解が一意に存在します.これを v(x,c) とします.
が存在します.開区間 (a k ,a k+1 ) において,f をa k+1 から ε だけ右側に連続になる様に適当に延長し,これを f’ として,(a k ,a k+1 +ε) で性質が良いとします.この f’ に対し,(a k ,a k+1 +ε) において,初期条件 φ(a k+1 )=c を満たす (1) の一般解が一意に存在します.これを u(x,c) と書きます.同様に,(a k+1 −ε,a k+2 ) で,左側に延長した f に対し,初期条件 φ(a k+1 )=c を満たす (1) の一般解が一意に存在します.これを v(x,c) とします.
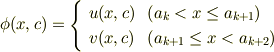
とおけば,φ(x,c) は,(a k ,a k+2 ) で連続な (1) の一意な一般解です.これを全ての不連続点で行えば,全体で連続な (1) の一意な一般解が得られます.
この φ は (1) を満たしているので,φ”=−fφ は …,a −2 ,a −1 ,a 0 ,a 1 ,a 2 ,… を除き連続で,各不連続点の跳びは有限です.従って, 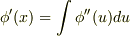 は,a k においても連続です.
は,a k においても連続です.
※toorisugari no Hiro さん,TeX のご指導をいただき,誠にありがとうございました.