電磁気学についての質問

電磁気学についての質問

たべめ さんの書込 (2006/11/05(Sun) 09:49)

はじめまして，ある私立大学の工学部に通っているものです．宿題で，このような問題が出されました．

「無限平板導体上に電荷が分布しているとする．一つの金属平板は電荷密度σが一様に分布し，もう一つの金属平板はアースにするとして，この二つの金属平板を並べると，各平板の上下方線方向における電場はどうなるかを求めよ」

金属平板が二つとも，電荷密度の値が決まっていれば，

重ね合わせの原理を適用するだけでいいんですが，アースが入ってくるとさっぱりわかりません汗

そのように解いたらいいでしょうか？ご教授のほどをよろしくお願いします．

Re: 電磁気学についての質問

のぼりん さんのレス (2006/11/05(Sun) 13:55)

こんにちは．自己の復習の意味も兼ねて考えてみました．門外漢の戯言ですので，頓珍漢かも知れません．その節はご容赦下さい．

アースした無限平板導体を ｘｙ 平面に，観測点を ｚ 軸上に取ります．帯電させた無限平板導体は，ｚ＝ａ＞０ のところにおきます．このとき，ｘｙ 方向への平行移動および ｚ 軸に関する回転に対して対称なので，以下，ｚ 軸方向のみ考えます．

アースした導体板は電位が ０ になります．ここで，アースした導体板を取り除き，−ａ のところに −σ に帯電させた導体板を置くと，ｚ＝０ における電位が ０ になるので，ｚ≧０ では鏡像の原理が使えます．ｚ＜０ では，ｚ＝０，ｚ＝−∞ の電位が双方とも ０ で，その間に電荷は存在しないので，常に ０ です．よって，ｚ における電位は，ＳＩ 単位系（ＭＫＳＡ）によると，

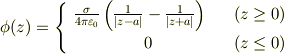
\phi (z) = \left\{\begin {array}{ccc}\frac {\sigma} {4 \pi \varepsilon_0} \left( \frac {1} {| z - a |} - \frac {1} { | z + a | } \right)\quad & \left(z \geq 0 \right) \\0 & \left(z \le 0 \right) \\\end {array} \right.

で，ｚ 軸方向の電場は

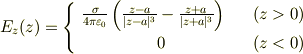
E_z (z) = \left\{\begin {array}{ccc}\frac {\sigma} {4 \pi \varepsilon_0} \left( \frac {z - a} {| z - a |^3} - \frac {z + a} { | z + a |^3 } \right)\quad & \left(z > 0 \right) \\0 & \left(z < 0 \right) \\\end {array} \right.

です．ｚ＝０ では微分できないので，特異点になると思われます．

※TeX は全く素人で，数式を書くのに難儀しています．式上段の文字を普通の大きさに表示したいのですが，やり方が判りませんでした．もしよろしければ，ご指導願えると助かります．

Re: 電磁気学についての質問

なんとなく さんのレス (2006/11/06(Mon) 10:13)

こんにちは． のぼりんさんの使われた電位（電場）の公式は点電荷に対するものです．無限平面の帯電した面密度分布の場合はそれをｘｙ平面で無限積分しなければならないと思いますよ． ところで，たべめさんの問題のように対称性が高く，一様な解が想像される場合，ガウスの法則を適用するのが一般的です．最初の金属平板1枚が面密度σで電荷が分布している場合，ガウスの法則より，電場はσ/2ε0となりますが，問題はもう１枚平板があることです．アースをつけるとは何を意味しているのかというと，電荷が移動して，アースをつけた導体と地面が同電位になると考えて良いということです． この問題の場合，もしアースをつけなければ，もともと電荷０の導体において，向かい合った電荷密度σの電荷に引かれ，近いほうに-σの電荷分布，導体の反対側に+σの電荷分布が追いやられて生じます（合計は常に０）．しかし，アースをつければ，+σはそれを伝って地面へ逃げることができ，結局導体には-σの電荷のみが残ることになります． したがって，この問題はそれぞれσ,-σに帯電した無限平面が向かい合ったケースと同じになると思います．これで計算できるのではないでしょうか．

TeX (Re: 電磁気学についての質問)

toorisugari no Hiro さんのレス (2006/11/06(Mon) 12:27)

のぼりんさん

> 式上段の文字を普通の大きさに表示したいのですが，やり方が判りませんでした．もしよろしければ，ご指導願えると助かります．

displaystyleをつかえばいいですよ． <pre><Tex> E_z (z) = left{ begin {array}{cc} displaystyle{ frac {sigma} {4 pi varepsilon_0} left( frac {z - a} {|z - a|^3} - frac {z + a} {|z + a|^3} right) } quad & left(z > 0 right) \[1.0em] 0 & left(z < 0 right) end {array} right. </Tex></pre>

E_z (z) = \left\{\begin {array}{cc}\displaystyle{\frac {\sigma} {4 \pi \varepsilon_0} \left( \frac {z - a} {|z - a|^3} - \frac {z + a} {|z + a|^3}\right) } \quad& \left(z > 0 \right) \\[1.0em]0 &\left(z < 0 \right)\end {array} \right.

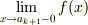
別スレッドの件になりますが， limについてはアンダーバーをお忘れです． <Tex>lim_{x to a_{k+1} - 0} f(x)</Tex> \lim_{x \to a_{k+1} - 0} f(x)

条件式の左揃えは begin {array} {ccc} を begin {array} {cl} にすればよいです．(そもそもすべてにcccを使われていますが，3カラムないので3個もパラメータはいらないです．)

Re: TeX (Re: 電磁気学についての質問)

のぼりん さんのレス (2006/11/06(Mon) 20:44)

なんとなくさん，ご指摘ありがとうございました． 確かに，この公式は普通の点電荷の場合のものですので，積分しなければいけませんでした．

ｚ’＝ｚ−ａ（＞０） とおいて，面積分すると，

E_z &= \frac {1} {4 \pi \varepsilon_0} \int_0^{\infty} \left(\int_0^{2 \varepsilon_0} \frac {1} {z'^2 + r^2}\frac {z} {\sqrt[3]{\mathstrut z'^2 + r^2} } d\theta \right) r dr \\&= \frac {z'} {2 \varepsilon_0} \int_0^{\infty} \frac {r} { (z'^2 + r^2)^{\frac {1} {3}} } dr \\&= \frac {z'} {2 \varepsilon_0} \left[ - \frac {1} {\sqrt {\mathstrut z'^2 + r^2}} \right]_0^{\infty} \\&= \frac {1} {2 \varepsilon_0}

となり，距離によらずに一定でしたね．電気力線が平行なので，当然こうなる訳ですし，そもそも，係数分母の ４π が消えなければならないことに気付くべきでした．ご迷惑をお掛けし，申し訳ありませんでした．

ｚ＝０ の接地導体板からの影響を合わせると，

E_z (z) = \left\{\begin {array} {cl}\displaystyle{- \frac {1} {\varepsilon_0}}\quad&\left(0 < z < a \right)\\[1.0em]0\quad&\left(z < 0 \vee z > a \right)\end {array}\right.
\phi (z) = \left\{\begin {array} {cl}0 \quad & \left(z \leq 0 \right) \\\displaystyle{\frac {z} {\varepsilon_0}}\quad&\left(0 \leq z \leq a \right)\\[1.0em]\displaystyle{\frac {a} {\varepsilon_0}}\quad&\left(z \geq a \right)\end {array}\right.

となりました．ここで，ポテンシャルは，接地面を ０ としました．

ｚ→∞ の無限遠の電位が ０ になりませんが，これは，無限に大きい導体板があり得ないことを意味していると理解しました．つまり，無限に大きい導体板とは，非常に大きい導体板をその付近で見た場合の近似であり，その近似では表式が成り立つが，導体板が小さく見える真の無限遠では，ポテンシャルは ０ に漸近していくものと考えました．

また，toorisugari no Hiro さん，ＴｅＸ のご指導をいただき，誠にありがとうございました．後程，別スレッドの方も修正しておきます．

Re: 電磁気学についての質問)

twister さんのレス (2006/11/07(Tue) 14:51)

のぼりんさん：

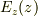私は，数学が弱いのですが，物理のサイドからの考え方を出して見ます．今，z=0のxy平面上に，薄い高分子膜が張られて，そこに面電荷 \sigma の電荷があったときに，z方向の電場 E_z(z) を求めようとすれば，クーロンの式から直接積分によって

E_z(z) &= \int_{r=0}^{\infty} \int_{\theta =0}^{2\pi} \frac {\sigma d\theta r dr} {4 \pi \varepsilon_0 (z^2 + r^2)} \frac {z} {(z^2 + r^2)^{1/2} } \\&= \frac {\sigma z} {2 \varepsilon_0} \int_0^{\infty} \frac {rdr} { (z^2 + r^2)^{3/2} } \\&= \frac {\sigma z} {2 \varepsilon_0} \int_{\xi=0}^{\infty} \frac {\frac{1}{2}d\xi} { (\xi + z^2)^{3/2} } \\&= \frac {\sigma z} {2 \varepsilon_0} \left[ \frac {1}{2}\cdot\frac{(\xi + z^2)^{-1/2}}{(-1/2)} \right]_{\xi=0}^{\infty} \\&= \frac {\sigma} {2 \varepsilon_0}

となりますね．ところが，高分子膜が金属に変わったとすると，状況が一変します．金属膜には裏と表があるからです．この場合でも裏面，表面からの寄与を直接に積分できるわけで，高分子膜の2倍の値になります．

＃高分子膜といったのは，絶縁できる膜，単に電荷を固定できる材料と言ったつもりです． ＃金属膜といっても，裏が透き通るほど薄い金属ではなくてバルクな金属の膜と考えます．

勿論，対称性を考慮して，マクスウェルの微分法則に対するガウスの発散定理から同じことが言えます．でも，常にクーロンの法則と電場の発散との関係を意識して，適用し易い式を利用するべきだと思います．

特に，物理屋は積分計算が不得意な人が多い(←自分の事)ので，ガウスの発散定理の結論だけを鵜呑みにしがちですが，電荷の分布から積み重ねて電場が出来ていることを忘れないようにしたいものです．

たべめさん：

話が飛びますが，静電誘導の立場からすると，ある金属に外部電場が入り込むには，その電場に相当する面電荷が金属表面に誘導されるイメージをもたれると良いと思います．とくにその金属が「アース」されるというばあい，「誘導された電荷の逆の電荷は，理想的にそのアースする物体に流れ出す」と考えるのだろうと思います．

以上，定性的な説明をさせていただきました．

Re: 電磁気学についての質問)

たべめ さんのレス (2006/11/07(Tue) 21:04)

たべめです．

皆さん，お答えいただきありがとうございました．後は自力で解いてみます．