歩き目です さんの書込 (2006/11/01(Wed) 23:31)

こんにちは． 今回は特にこれといった質問ではないのですが， 有効数字についてです． この間帰ってきた模試でも答えが9.48×10の？乗 というような答えのところで9.49×…と答えてしまい バツを食らっていました． 掛け算や割り算の途中経過でどう処理していけば いいのかがわかりません． 一桁多く取って切り捨てた値を用いて計算など色々な 噂は聞くのですが…． 例えばですが，9.85÷4.72×3.88を有効数字3桁で答えよ． (数値は適当です．)という場合． 9.85÷4.72=2.086864…となるのですが，この値をどう処理して ×3.88すればいいのでしょうか？

カリプソ さんのレス (2006/11/02(Thu) 00:32)

こんばんは．いつもこの掲示板にはお世話になっているカリプソです．いつも助けてもらう側なので，参考程度に読んでください．

有効数字の指示があった場合は，計算過程にはその桁の一桁多くとればいいと思います．その次は切り捨てです．例えば，9.85÷4.72=2.086864…は，指示が３桁なので9.85÷4.72≒2.086（その次の８は切り捨て）とすればいいのではないでしょうか．それに3.88をかけて，４桁目を四捨五入して３桁にすればいいと思います． ちなみに，有効数字の指示がない場合は，問題文に出てくる数値の中で桁が一番小さなものに合わせます．

前述しましたが，いつもは質問ばかりしている身ですので，他の方にも助言を求めます．宜しくお願いいたします．

なんとなく さんのレス (2006/11/02(Thu) 13:11)

こんにちは．

有効数字３桁とは通常，○.○○×10^○・・と表して，最初（1の位）が「０」でないように出来るものと考えればよいのではないですか． したがって， 9.85÷4.72=2.0868・・・は，2.09とすべきで，そのあと， 2.09×3.88=8.109・・・より，答えは8.11であると思います． つまり，途中計算も同様に，有効数字にまるめて（四捨五入して）計算するのが正しいのではないでしょうか． 誤差の伝播理論から言って，途中に桁を多くとることは意味が無い気がします． 蛇足ですが，有効数字はいつも可能とはかぎりません．減算，割算では良く知られた，「桁落ち」によって有効数字は減少する場合があります．答えに約をつけるべきか否かは問題文次第かなあ．

歩き目です さんのレス (2006/11/02(Thu) 16:45)

お答えありがとうございます． でも，お二方の意見のどちらが正しいのでしょうか？

ｙama さんのレス (2006/11/02(Thu) 17:10)

有効数字というのは，かなりおおざっぱで便宜的なものです． 精度が10倍になれば，有効数字が1桁増えるので，次の桁までとることができます． しかし，精度が２〜３倍になった場合はどうでしょうか． 10倍にまではなっていないので，有効数字をそのままにすると，精度の向上が数値に反映されません． しかし，1桁増やすと数値の精度に比べて有効数字が多過ぎます． このように，有効数字は数値の精度を正確に反映するものではなく，おおざっぱな目安として示しているだけです． 正確な取り扱いでは確率誤差とか標準誤差とかを考慮した計算が必要です．

このように，おおざっぱな目安と考えると，なんとなくさんのような取扱いもできるでしょう． しかし，普通は途中の四捨五入などによる誤差ができるだけ少なくなるように計算します． そのため，計算途中では，有効数字より１〜2桁多くとって計算することが多いようです． これには次のような場合が考えられます． ? 有効数字より２桁余分に計算する．すなわち 9.85÷4.72=2,0868 とする． ? 有効数字より２桁余分に計算し，最後の桁を四捨五入する．すなわち 9.85÷4.72=2,087 とする． ? 有効数字より１桁余分に計算する．すなわち 9.85÷4.72=2,086とする．

それぞれの数値に 3.88 を掛けて有効数字３桁で表すと?と?は 8.10，?は8.09になります．当然?→?→?の順に高精度で，また同じ順に計算に手間がかかります． カリプソさんの方法は?ですね． どの方法がいいとは一概にはいえませんが，入試の場合はどれでも許容範囲だと思います．しかし，なんとなくさんのやり方では誤答とされるかもしれません．

入試に限れば，途中ではなるべく四捨五入しないで，最後に四捨五入するように工夫するのがいいと思います． つまり9.85×3.88を計算してから，そのままの数値を4.72で割って有効数字３桁で表すわけです．結果は 8.10 となります．

なんとなく さんのレス (2006/11/02(Thu) 18:10)

yamaさん，丁寧な解説だと思います．

私も高校生の頃，入試では有効数字が指定してあったら，1桁ほど余分に計算して最後に丸めろ，と習いましたっけ．yamaさんの仰るとおりでしょう．しかし，物理での有効数字は大雑把な目安ではなく，むしろ逆にここまでしか精度が保障できない，あるいはここまでは確かだ，と主張する積極的な表現ではないでしょうか． 論文等に書かれた有効数字は強力な主張をします．なぜ素粒子の質量や電荷の数値に有効数字を上げる努力がいつまでも続けられるのか，系統誤差や計算誤差の極限まで真値を得ようとするのか，その心を忘れないでいるためにも，敢えて主張しました．入試という枠に囚われないで欲しいという老婆心ですが，現実は・・・． 本来，有効数字を指定された桁以外の数値で計算するのなら，どの桁まででというコンセンサスがなければならないし，そうでないなら複数の解等も許容すべきでしょう．「×」は酷いと思いますが，それが模試の正体かな．

歩き目です さんのレス (2006/11/02(Thu) 19:01)

yamaさん，なんとなくさん，お早いお答えありがとうございます． >>入試の場合はどれでも許容範囲だと思います． わかりました．とりあえずは?のやり方でやっていこうかなと思います． >>入試に限れば，途中ではなるべく四捨五入しないで，最後に四捨五入す るように工夫するのがいいと思います． うーん．なるべくそうしようと心がけていこうとは思いますが，時間的に 少し厳しいような気もします．

toorisugari no Hiro さんのレス (2006/11/02(Thu) 19:05)

> 物理での有効数字は大雑把な目安ではなく，むしろ逆にここまでしか精度が保障できない，あるいはここまでは確かだ，と主張する積極的な表現ではないでしょうか．

それは有効数字ではなく誤差で表現するべきものでしょう．

ただ，私も実験の専門家でないので，誤差を出すとき「誤差の桁」をどうするか，つまり，誤差の有効数字をどれだけ採るかについて，よく悩みます．

簡単なルールがあればどなたか教えていただけないでしょうか．

なんとなく さんのレス (2006/11/03(Fri) 00:02)

>toorisugari no Hiroさん

私も実験系の方の論文の書き方やルールには疎いので，想像に過ぎませんが，もしかするとルールは無いのかも知れません．しかし，実験精度の主張として誤差が積極的な表現だというのはムリがありませんか．確かに主張には違いないですが，消極的なものであると思います． 例えば，自由電子のｇ因子，例えば超微細構造，例えばエディントン卿の相対論検証など，その精度が理論の分かれ目になる実験・観測は多々あれど，誤差が理論を主張することは稀でしょう． ご存知とは思いますが，ＱＥＤの目覚ましい評価はその予言精度の高さに尽きると言えるでしょう． たかが有効数字の扱いではありますが，理論の正当性を裏付ける唯一の方法が実験による検証である限り，有効桁数を上げることが目指すべき目標であると言うのは言い過ぎでしょうか．

カリプソ さんのレス (2006/11/03(Fri) 00:11)

>>入試に限れば，途中ではなるべく四捨五入しないで，最後に四捨五入す るように工夫するのがいいと思います． うーん．なるべくそうしようと心がけていこうとは思いますが，時間的に 少し厳しいような気もします． 計算過程では切り捨てすればいいので寧ろ楽になるのではないでしょうか．

>それは有効数字ではなく誤差で表現するべきものでしょう

確かに入試で指定された有効数字と実験時の誤差の扱いは別ものだと思います．受験問題での有効数字については出題者の方もあいまいにしているケースも少なくないようです．

＞簡単なルールがあればどなたか教えていただけないでしょうか． 受験時に使っていた書物に参考になるのではないかと思われるものが載っています．よろしければスキャンして送信しますけれど．．．

ｙama さんのレス (2006/11/03(Fri) 08:53)

数値の精度を正確に表すには，誤差を明記するのが普通だと思います． たとえば，理科年表ではプランク定数が 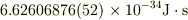とされていて()内の 52 が最後の2桁の標準不確かさを表すとされています． 最後の２桁は不確かなので，有効数字だけで精度を表せば 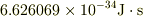になると思いますが，これでは正確な精度はわかりません．

なんとなく さんのレス (2006/11/03(Fri) 10:32)

こんにちは．

勿論，一般的に実験値でも理論値でも，物理量の値と誤算は一対で意味を為すもので，それを否定してるわけではないのです．何故，高校物理で有効数字という概念が用いられるのか，何故「およそ〜」とか「約〜」で済まさないのか，それを入試という形で問うのは如何なる根拠に基づくものか，ということです． 指導要領にあり計算法が明記してあるなら何らかの狙いと習熟度の判定が必要でしょう．それがここで議論されるように曖昧模糊としている．更に言えば入試のテクニックという実用性で正否が定められる，そこに反骨（偏屈？）回路が反応したまでです． 自分で書いてて，ちょっとイヤになった（こちらへお邪魔するとなぜかウザイおやじになってしまう）ので，もう止めますが，要は物理の問題においては最初の質問にあったように誤差の範囲内のような回答に「×」が付くことの無いようなコンセンサスができればいいなあ，と思うのです．

カリプソ さんのレス (2006/11/03(Fri) 19:09)

＞要は物理の問題においては最初の質問にあったように誤差の範囲内のような回答に「×」が付くことの無いようなコンセンサスができればいいなあ，と思うのです． まったくもってそうだと思います．入試では許容してくれるのではないかと勝手に思っていますが．模試は何万という答案をこれまた多くの，あちこちの方々が採点するので，どこまで許容するか等の統一が難しく，模範回答以外は×をつけることになっているのではないでしょうか．

これは私事ですが，，，，いつも質問してお世話になるだけだったので，今回初めて討論的なことに加われたことをうれしく思います．今後とも宜しくお願いします．

山旅人 さんのレス (2006/11/04(Sat) 00:14)

>> 歩き目です さん 皆さんの議論をご理解いただけますでしょうか？私は，別の観点から…．

9.85，4.72，3.88 の数値に測定に起因する誤差が与えられていない場合，それらは， 9.845≦x＜9.855， 4.715≦y＜4.725， 3.875≦z＜3.885 である量 x，y，z を symbolize しているもの（記号） とみるべきでしょう．そうすると， xz/y は，8.073942＝9.845×6.875/4.725＜xz/y＜9.855×3.885/4.715＝8.120186 … (*) である可能性があります．

9.85/4.72＝2.086864 を１桁余分にとり，余分の２桁目を切り捨てて 2.086 とすると 2.086×3.88＝8.097034 となり，最終的にこれの４桁目を四捨五入して 8.10 とすることが，(*)から考えて最も妥当だと思います． すなわち，計算の途中では，<b>１桁余分にとり，余分の２桁目を切り捨てる</b> カリプソ さんの方法がよいと思います．

歩き目です さんのレス (2006/11/04(Sat) 19:41)

山旅人さん，ありがとうございます． 自分のくだらない質問がいつの間にかはるかに高校生の理解の範疇に ないところまで飛躍していてびっくりしていましたが，それも有効数 字の重要さゆえのものなのでしょうね． 山旅人さんのアドバイス通り１桁余分にとり，余分の２桁目を切り捨 てるというカリプソさんの方法でいきたいと思います． 皆さんには高校三年生の素朴な疑問にこんなに真剣に議論していただ き本当に感謝しています．ありがとうございました． 明日はセンター模試です．マーク式なのでさすがに0.01の違いで間違 うことは無いと思いますが，全力を出せるよう頑張ってきます． では，また疑問が生じたときは書き込みますのでよろしくお願いしま す．

山旅人 さんのレス (2006/11/04(Sat) 22:42)

>> なんとなく さん > 何故，高校物理で有効数字という概念が用いられるのか，何故「およそ〜」とか「約〜」で済まさないのか

あなた自身のレスの中にこの問の回答がある，と私は思いました．すなわち，

物理での有効数字は大雑把な目安ではなく，むしろ逆にここまでしか精度が保障できない，あるいはここまでは確かだ，と主張する積極的な表現

私もその通りだと思います．高校生に有効数字の意義を問われたら，私は，

2.3 … 2.25 ≦x＜2.35 2.30 … 2.295 ≦x＜2.305 2.300 … 2.2995≦x＜2.3005

「精密さが違うのだよ」 と答えることにしています．

> 物理の問題においては最初の質問にあったように誤差の範囲内のような回答に「×」が付くことの無いようなコンセンサスができればいいなあ，と思うのです．

同感です．

なんとなく さんのレス (2006/11/05(Sun) 00:55)

>山旅人さん，カリプソさん，レス有難うございます．

実際的にカリプソの方法で，その根拠は別な視点どころか将にピンポイントで山旅人さんの考え方で十分だと思います．他の方の反論も正当ですし，私自身には疑義はありません．ご存知とは思いますが，試験問題の解答は，その数値までもコントロールし，良問では，例えば今回の問題のような場合，許容範囲の計算方法に対してユニークな解になるよう工夫してあるものです．昨今は逆にわざと紛らわしい数値を配置し，どこかのテクニックに従わないと「×」になるよう，正解が人為的に操作されている傾向がある（様な問題がある）気がします． これは受験者側の人に向けて言うことではないけれど，そんな世界に振り回されないよう，試験がんばって欲しいものですね．そして物理をイヤにならないで欲しいと思います．歩き目ですさん，頑張って．では，また．

yama さんのレス (2006/11/06(Mon) 21:08)

有効数字というものをを厳密に取り扱うことができるかどうかはちょっと疑問です．

たとえば 9.85÷4.72×3.88 を有効数字３桁で表すと 8.10 になるというのはどういうことでしょうか？ この３桁までは確実に保障できるとすれば 8.095≦真の値＜8.105 でないといけません． しかし山旅人さんの計算結果を借用すると 8.073942＜真の値＜8.120186 なので，３桁目は確実には保障できないことになります． つまり確実に保障できるのは２桁の 8.1 なので，有効数字は２桁ということになります． しかし，普通は有効数字は３桁と考え，8.10 とすることが多いようです． その場合の３桁目は確実には保障できないにしても，ほぼその数字に近いだろうという目安だと思います．

なんとなく さんのレス (2006/11/06(Mon) 23:51)

>yamaさん．

>>つまり確実に保障できるのは２桁の 8.1 なので，有効数字は２桁ということになります

有効数字３桁というのは，２桁めまでが保障できて３桁目は仰るように近しい，もっともらしい場合に言うのだと思っていましたが．つまり，上記以降に書かれたことこそ有効数字３桁のことだと思うのですが． 定義が違うのかしら？

ｙama さんのレス (2006/11/07(Tue) 10:41)

確かにその通りだと思います． しかし，高校の教科書などでは，そのあたりの取扱いが曖昧で，初めは有効数字の最終桁の誤差が ±0.5 以内であるかのように説明しながら，いつのまにか最終桁は目安であるような取扱いになります．

しかし 9.85÷4.72×3.88 の計算で各数値の３桁目が目安で，最大で±２程度の誤差があるとすれば真の値は 9.83÷4.74×3.86=8.005 から 9.87÷4.70×3.90=8.190 の範囲にあることになります．この場合，確実なのは最初の1桁の８だけなので，２桁目は目安だということになります．つまり有効数字は２桁になってしまいます． このように，真の値が確実に存在すると考えられる範囲によって有効数字を決めるならば，計算を繰り返すほど真の値が存在すると考えられる範囲が広がるため，有効数字の桁数が少なくなってしまいます．

このようなことを避けるには，真の値が確実に存在すると考えられる範囲によって有効数字を決めるのではなく，真の値が高い確率で（たとえば50％以上の確率で）存在すると考えられる範囲によって有効数字を決めればいいわけです． 計算例の場合，真の値が 8.005 とか 8.190 に近くなる可能性はあるとしても，その確率は極めて小さく，8.10を中心とした狭い範囲に存在する確率が大きいので，有効数字を３桁と考えるわけです．もちろん厳密には，誤差をきちんと考慮した計算が必要です．

高校の教科書では，このような確率的な考慮がされていないので，どうしても説明に無理が生じるのだと思います．

なんとなく さんのレス (2006/11/07(Tue) 12:08)

yamaさん，レス有難うございます．

>このように，真の値が確実に存在すると考えられる範囲によって有効数字を決めるならば，計算を繰り返すほど真の値が存在すると考えられる範囲が広がるため，有効数字が少なくなってしまいます

はるか昔なのと不勉強のため確実ではないのですが，まさにそのような事態を避ける処方が誤差論に基づいた有効数字の発祥であると思います．

>高校の教科書では，このような確率的な考慮がされていないので，どうしても説明に無理が生じるのだと思います．

なるほど，それはひとつの見解です．教師がと言えば語弊があるでしょうが，教育する側が高い意識を持たねば，そこら辺はうやむやになってしまいますね． 私ももう一度考え直してみたいと思います．では，また．