サイクロトロン放射
サイクロトロン放射
のぼりん さんの書込 (2006/10/26(Thu) 21:34)
お世話になっています.川村「電磁気学」(岩波) の演習問題に取り組んでいます.
【問題文】角速度 ω で半径 a の軌道上を円運動する荷電粒子が 1 周期に放出によって失うエネルギーを求めよ.ただし,粒子がもつ電気量を q とし,1 周期の間に粒子の角速度は変わらないものとする.
【略解】(9.42) を立体角について積分すると, 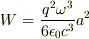
ここで,(9.42) とは, 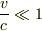 のときに近似的に成り立つサイクロトロン放射の式
のときに近似的に成り立つサイクロトロン放射の式
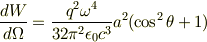
で,θ は回転軸を z 軸として測った立体角方向の角度,dW/dΩ は単位時間に放出される立体角当たりのエネルギーです.この式の導出は理解できていると思います.
さて,略解どおりに計算すると, 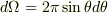 で,一周期の長さは
で,一周期の長さは 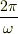 だから,
だから,
![W &= \frac {2 \pi} {\omega} \int_{0}^{\pi} \frac {q^2 \omega^4} {32 \pi^2 \epsilon_0 c^3} a^2 (\cos^2 \theta + 1) \cdot 2 \pi \sin \theta d \theta \\&= \frac {q^2 \omega^3 a^2} {8 \epsilon_0 c^3} \left[ - \frac {\cos^3 \theta} {3} - \cos \theta \right]_{0}^{\pi} \\&= \frac {q^2 \omega^3 a^2} {8 \epsilon_0 c^3} \frac {8} {3} = \frac {q^2 \omega^3} {3 \epsilon_0 c^3} a^2](http://hooktail.maxwell.jp/bbslog/3a0e6c9a1efff6863a8b7378a2be0f01.png)
と,略解の二倍が得られてしまいます.どこか間違っているのでしょうか?
普通でしたら,単なる誤字だろうと考えるのですが,この後同式が他の箇所でも引用されています.そう考えると,略解の結果が真実なのだろうと思うのですが,上記計算の不備がわかりません.どうやると,略解の結果が得られるか,ご教示願えませんか?
意図せず連続投稿になってしまい,申し訳ありませんが,何卒よろしくお願い申し上げます.
Re: サイクロトロン放射
のぼりん さんのレス (2006/10/27(Fri) 21:31)
サボテンさん,計算確認の労をお執りいただき,どうもありがとうございました.元々の式は,一般的な式
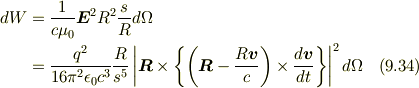
を前提として,以下のとおり導出されています.ここに, 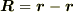 は荷電粒子
は荷電粒子 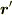 から観測点
から観測点  へ向かうベクトル,また
へ向かうベクトル,また 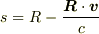 です.
です.
簡単のために, 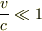 であるとする.このときは,
であるとする.このときは, 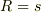 としてよいから,
としてよいから, 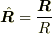 として,
として,
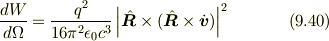
である.荷電粒子の円運動の面を xy 面内に選んで,
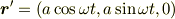
とすると,
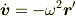
である.荷電粒子は z 軸を中心にしているのであるから,電磁場を観測する場合は xz 面内であると考えても一般性を失わない.そこで,z 軸を極軸とする極座標を使って,
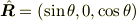
と表すことにすると,
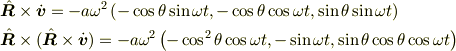
と計算されるから,
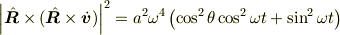
である.この結果を (9.40) の右辺に代入すると,
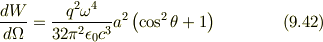
となる.
以上を見る限り,(9.42) の導出過程も納得できる様に思えるのですが,いかがでしょうか?
Re: サイクロトロン放射
サボテン さんのレス (2006/10/28(Sat) 08:11)
のぼりんさん,計算に至る詳細な過程をお書き頂きありがとうございました.
計算を確認しましたが,特に間違いはないようです. 私の力ではお手上げです.大変申し訳ありません.
Re: サイクロトロン放射
のぼりん さんのレス (2006/10/28(Sat) 08:41)
サボテン さん,昨日に引き続いて疑問点の確認をいただき,誠にありがとうございました.数学的には導出過程に問題なさそうだったのですが,ひょっとして,私の知らない物理の原理等が使われているのでは,と思い,再質問した次第です.
本件疑問については,解決を諦めることとします..・゜・(/Д`)・゜・.
今後とも,何卒よろしくお願い申し上げます.
Re: サイクロトロン放射
twister さんのレス (2006/10/28(Sat) 17:18)
大変気になったので,近くの図書館で電磁気の図書を見てみました.
「電磁気の物理,清水 忠雄・著,朝倉書店,ISBN 4-254-13585-8」の「§21 運動する電荷からの電磁波の放出」によれば;
粒子が単位時間に放出する全エネルギーは,

と在ります.
他方,円運動であれば,
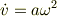
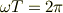
ですから,円運動の1周期に付いてのエネルギー放出量Wを考えれば,
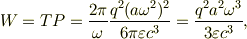
となるように思います.
Re: サイクロトロン放射
のぼりん さんのレス (2006/10/28(Sat) 20:25)
twister さん ありがとうございました!ヾ(●´∀`●)ノ 調査の労をおとりいただき,本当に感謝します.
ということは,略解の結果が,真の結果の二分の一になってしまっている訳ですね. その後の結果も調整が必要と言うことが,納得できました. 今後ともよろしくお願いします.(*・艸・).+:*○
Re: サイクロトロン放射
サボテン さんのレス (2006/10/29(Sun) 07:36)
twisterさん 調査して下さったんですね!勉強になりました.ありがとうございます.
のぼりんさん
計算結果が正しかったようで何よりです.私も数年ぶりに物理の計算を しました(^^;) いい練習になりました.
Re: サイクロトロン放射
twister さんのレス (2006/10/29(Sun) 09:36)
お二人の論議につられて調べてしまいました.
ただ,お分かりのように,自分は細かな計算の裏づけをした上での発言ではありません.従って,可能性としては,のぼりんさんの計算が正しいらしいという指摘をさせていただいただけです.
問題の鍵は, 『【略解】(9.42) を立体角について積分すると』 という所ではなかろうかと推察します.
著者は,ワザと円運動の寄与を簡単に記述して,時間平均をする項目を1/2にして,読者に探させようとしたとか(笑).
いずれにしろ,キチンと計算する読者にとって困ることですので,略解について検討されると面白いかもしれませんね.
のぼりんさんの疑問の立て方,問題を解くときの考え方は「とても物理的」だと感じています.この調子で,「おかしいな!」と感じた点を,サボテンさんや他の論客の方々と議論されると,勉強中の他の方々にも元気を与えると思います.