スピンについて

スピンについて

のぼりん さんの書込 (2006/10/24(Tue) 22:53)

こんばんは．お世話になっています．さて，電子等のスピンについて，教えていただければと思います．

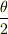スピノルの数学的意味合い等については一応学習したのですが，スピンの物理的意味合いがどうにも納得できません．３次元スピノルは，ＳＵ（２） で回転を受ける <b>C</b> 2 の元であり，座標系を \theta だけ回転すると，その成分が \frac{\theta}{2} だけ回転を受けます．これは良いとして，実際に観測する際，どうなるのでしょうか．

先ず，座標系を回転させることの意味ですが，例えば試料の正面から観測していたものを，右側から観測すれば，９０°だけ座標系を回転させた，と考えて良いでしょうか．

そうだとして，スピンを観測する機械を二台用意し，一台を固定しもう一台を少しずつ標本の周りを回転させていきます．９０°回転させると，成分は４５°だけ回転した結果が得られるということでしょうか．もしそうだとすると，徐々に回転の角を大きくしていき，一周すると，固定していた機械で上向きのスピンが観測された場合，もう一台では下向きのスピンが観測されることになりますが，こんなことが実際にあり得るのでしょうか．

物理の教科書を何冊当たっても，具体的な記述に欠けていてイメージが湧きません．専門の皆様には常識的なことなのかも知れませんが，自習している者にとって，とてもハードルが高く感じます．何卒ご教示下さい．

※ネットを漁っていたら，スピンの発見者の一人である Goudsmit（ハウシュミットと発音するのでしょうか？）の講演録がありました： http://www.lorentz.leidenuniv.nl/history/spin/goudsmit.html 中々面白い内容でしたが，残念ながら私の疑問には役に立ちませんでした．

Re: スピンについて

山旅人 さんのレス (2006/10/25(Wed) 00:16)

のぼりんさん，こんばんは．

現在は絶版で手に入らないのですが，図書館で 『スピンはめぐる』−成熟期の量子力学−（朝永振一郎・著，中公自然選書） を是非ご覧下さい．

神保町の古書店でも探す価値あり．

Re: スピンについて

ｙama さんのレス (2006/10/25(Wed) 09:09)

スピンとスピノルが混同されているようですが・・・．

スピンが1/2の粒子では，スピンの上向きおよび下向きに対応する２つの波動関数を考えることとができます．座標系の回転に対して，これらの波動関数は互いに関連しあって変換するので，これらをまとめて２成分からなる１つの量として考えたものがスピノルです．

座標系の回転に対してスピン自体が θ/2 回転するわけではありません．

Re: スピンについて

サボテン さんのレス (2006/10/25(Wed) 14:17)

http://www.aa.alpha-net.ne.jp/t2366/%83X%83s%83m%81 [%83%8B.htm

あたりが参考になると思います．

yamaさんがご指摘の通り，スピンがθ/2だけ回転するわけではありません．

また，z軸方向のスピンを観測している場合「45度だけ傾いた状態」 が観測されることもありません．z軸方向に対して上か下か(電子の場合) が得られるだけです．

但し，のぼりんさんがご指摘のように360度回転すると，スピノールの 波動関数には-1がかかります．その意味で波動関数は多価関数です． しかし，実際の観測量は波動関数はノルムですので，スカラー倍は影響しません． 同じ状態を表します．

量子力学に関しては，私の理解が至ってないところもあり，回答をつけるのも お恥ずかしい限りですが，ご参考になれば幸いです．

Re: スピンについて

のぼりん さんのレス (2006/10/25(Wed) 21:14)

皆さん，数々の助言を賜り，誠にありがとうございました． 専門家の皆様のご指導が得られ，心から感謝しています．

山旅人さん

助言ありがとうございました． 「スピンはめぐる」の名声は夙に聞いていたのですが，手に入らず今に至っていました． ご助言に従い，早速，神保町に出向いてみました． 十軒以上聞いて回りましたが，残念ながら発見できませんでした． その代わり，古本・新本を何冊か衝動買いしてしまいました（笑）．

ｙama さん

ご指摘ありがとうございました． 仰るとおり，質問内容が悪かったです． 回転するのは存在確率（波動関数）であり，実際の観測値ではありませんね． 頭の回転が悪くて未だ納得できていないので，もう少しに考えてみます． その結果，またおじゃまするかも知れませんが， その節はよろしくお願いします．

サボテンさん

ご紹介いただきありがとうございました． 同サイトを早速読んでみたいと思います． 大助かりです．

Re: スピンについて

山旅人 さんのレス (2006/10/25(Wed) 22:49)

のぼりんさん，こんばんは．

> 残念ながら発見できませんでした

そうですか，購入する道は閉ざされてしまったわけですね．残念です． ならば，図書館しかありません．もしお近くの図書館になければ，最後の手段ですが，国立国会図書館にはあります．

ところで，『スピンはめぐる』 はだめでも，『角運動量とスピン』（朝永振一郎遺稿，みすず書房）は，現在でも手に入るようです． 前者は一般の読者向けに書かれたもの（雑誌「自然」に連載されていた）ですが，後者は完全な専門書です．ですが 4,305円と高いので，これも図書館で内容を確認されてからの方がよろしいでしょう．

Re: スピンについて

いち さんのレス (2006/10/26(Thu) 01:53)

便乗質問させてください．

スピンに上向き，下向きしかないというのは，結局のところ， 「上向き，下向きしか測定できないから」 ということなんでしょうか．

そんな単純なことではないとは思うのですが・・・

Re: スピンについて

ｙama さんのレス (2006/10/26(Thu) 11:35)

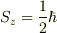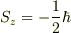上向きと下向きしかないのは，スピン1/2の場合だけだと思います． この場合，スピンのz成分の固有値が S_z=\frac{1}{2}\hbar と S_z=-\frac{1}{2}\hbar の２つしかないからです．

スピンが１の場合は 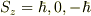S_z=\hbar,0,-\hbar の３通りあるので，スピンの向きは，上向き，横向き，下向き の３通りが可能です．

Re: スピンについて

いち さんのレス (2006/10/26(Thu) 12:29)

yamaさんありがとうございます．

その，スピン１の場合も結局のところ，ハグレ陽子のスピン1/2とハグレ電子1/2の 磁場で上向き，下向き決められて足し算，引き算されただけのようにしか思えない のです．

ですので，また，この精度でしか測れないんだから上向き，下向きなんでは？ と思ってしまいます．

ところで，シュテルン・ゲルラッハ実験の四重極マグネット版みたいなのを作る と４方向に分かれたりしないんでしょうか．

Re: スピンについて

いち さんのレス (2006/10/26(Thu) 12:42)

物理学辞典によると，中性子のスピンも1/2なんですね． これは，クオークが水分子みたいな感じになってるってことなんでしょうかね．

Re: スピンについて

ｙama さんのレス (2006/10/26(Thu) 17:30)

複合粒子の場合は，足し算や引き算で考えることもできると思いますが，ゲージボソンの場合は今のところ素粒子と考えられているので，その考え方は適用できないでしょう． いずれにしても，複合粒子でも素粒子でも，スピンのz成分の固有値が全スピンによって決まるという点は同じであって，測定精度の問題ではないと思います．

「クオークが水分子みたいな感じになってる」というのがよく分かりませんが，水分子のスピンは1/2なのでしょうか？0のように思えるのですが・・・．

Re: スピンについて

いち さんのレス (2006/10/26(Thu) 18:18)

yamaさん

>「クオークが水分子みたいな感じになってる」というのがよく分かりませんが，水分子のスピンは1/2なのでしょうか？0のように思えるのですが・・・．

これはスピンというよりも磁気モーメントだったんですけども， 物理学辞典によると，磁気モーメントが０ではないんで，はて？と 思ったところです．

Re: スピンについて

のぼりん さんのレス (2006/10/26(Thu) 21:02)

高度な議論の中，低級な話題で申し訳ありませんが…

山旅人さん

なるほど．朝永先生の本ですか！知っていれば買ったのですが，残念ながら昨日，ファインマンを買ってしまいました．ファインマンはスピンに二章を割いていて，シュテルン・ゲルラッハの実験について詳しく触れています．まだ読み出したばかりですが，漸くスピンの観測の意味を実例で知ることができ，わかりかけてきた様に感じています．手持ちの本（猪木・河合，Ｄｉｒａｃ，河原林，３０講，原島等々）は，この当たりを飛ばしており，実感が湧かず困っていたところでした．量子力学の本ばかりやたら溜まってしまい，何れ処分しないと… 国会図書館は拙宅から比較的近いですが，取り敢えずファインマンから取りかかってみます．

先に ｙama さんに指摘いただいたとおり，スピンとスピノルの対応関係が理解できていなかったのだと思います．まだ理解が行き届いていないとは思いますが，今まで納得した範囲では，以下のとおり解釈しています．

シュテルン・ゲルラッハの装置を使い，上向きスピンを有する電子のビームのみ抽出します．その先に１８０％反転したシュテルン・ゲルラッハの装置を接続して，スピンの向きを観測します．最初の装置で，電子ビームは，固有状態

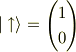
| \uparrow \rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix}

のもののみになります．次の装置は，Ｏ（３） の １８０％ 回転ですから，ＳＵ（２） では ９０％ 回転になり，

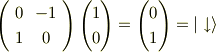
\left(\begin {array} {ccc} 0 &-1 \\1 & 0 \\\end {array} \right)\begin{pmatrix} 1 \\ 0 \end{pmatrix}= \begin{pmatrix} 0 \\ 1 \end{pmatrix}= | \downarrow \rangle

のみ観測されます．これは，下向きスピンのみの固有状態です．反転して下向きが観測された訳ですから，元に戻して考えれば上向きと解せます． この様な理解で良いでしょうか？

Re: スピンについて

サボテン さんのレス (2006/10/27(Fri) 07:45)

私も浅い理解しかできていないのですが，それで良いと思います．

これはおせっかいかもしれないのですが，のぼりんさんのように数学に お詳しい方は，場の量子論から入られた方がしっくり来るかもしれません．

Weinbergの「場の量子論」では各量子場をローレンツ群の表現から 捉えることで導入しています．スピノール場もそこではローレンツ群の 1つの表現として自然に導入されています．

Re: スピンについて

のぼりん さんのレス (2006/10/27(Fri) 21:30)

サボテンさん，確認いただきありがとうございました．安心しました．また，各掲示板でのご活躍，すごいな，と思って拝見しています．

さて，「数学に詳しい」などと過分な評価をいただきましたが，実際の所，大学では数学を専攻していた，というだけのことで，大して詳しい訳ではありません．大学教育は証明に偏っており，実際の計算となると，全く駄目です．その上，物理的常識が全くありませんので，抽象的な話になると，残念ながらついていけないでしょう．暫くは，初等的な本を中心に基礎から学習してみようと思っています．

お節介などと，とんでもない！助言ありがとうございます．ご紹介いただいたワインバーグの「場の量子論」とは，吉岡書店から刊行されているシリーズもののことでしょうか？本屋に並んでいるのは何回か目にしたのですが，敷居が高く手にとって眺めたことはありませんでした．スピノル場をローレンツ群の表現として導入しているとの由，とても興味があります．この様な高度な全集が読める日が，何時か来ることを期待しています．

Re: スピンについて

サボテン さんのレス (2006/10/28(Sat) 07:43)

私は，のぼりんさんこそ凄いと思ってお答えを拝見し，いつも参考にさせて 頂いています．また物理に対する向学心に感服しております．

私は病気の為，物理を捨てて，今は関係のない仕事をしています． 数年経って数学の勉強をしたくなり，掲示板にて皆さんとご一緒に勉強している 次第です(ですので，数学は初歩からやらないと分かりません)

とは申しましても，のぼりんさんの勉強に対する意欲には到底及ばないでしょう． 世の中には素晴らしい方々がいらっしゃることを知り，感慨ひとしおです．

場の量子論はご指摘の通り，吉岡書店のものです． あと物理的イメージを掴むなら，ファインマン物理学は面白いです． (もう量子論に関してはお持ちのようですね．)

是非またのぼりんさんに色々とご教示頂きたいです．宜しくお願い致します．