Chippy さんの書込 (2006/10/24(Tue) 20:04)

すいませんがどなたかこの問題の解き方を教えていただけないでしょうか．

speed， the angular momentum，the orbital frequencyなどの公式の求め方授業でも習ったことが無くかなり困っております．

The tau particle is a negatively charged particle similar to the electron (i.e. charge = -e), but of much larger mass. Its mass is 3.18e-27 kg, about 3490 times that of the electron. Nuclear material is transparent to the tau; thus, the tau can orbit around inside a nucleus, under the influence of the electric attraction of the nuclear charge. Suppose that a tau is in a circular orbit of radius ｒ m inside a uranium nucleus. Treat the nucleus as a sphere of radius Ｒ m with a charge of 92e uniformly distributed over its volume. Recall that Gauss' theorem is

日本語訳：負の電荷,(-e)を帯びたτ粒子があり．その重さは3.18e-27 kgででんしの3490倍の重さに相当する．τ粒子はウランの中性子の内側（ｒ）ｍを周っており．そのときの中性子の半径 は(Ｒ)ｍで，９２eの電荷を球内中に均一に（まんべんなく）帯びています．

q_enc= (ε_0)∫E・dAを用いて以下の問題の公式を求めなさい．

Find the speed?

Find the angular momentum?

Find the orbital frequency?

tadash さんのレス (2006/10/25(Wed) 00:14)

speedは等速円運動の運動方程式から the angular momentumはｍｖ×ｒ(外積)を用いて the orbital frequencyは一周( 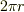)する間にｖＴ進むこと， frequencyがtime の逆数であることを用いて 導き出せると思います． よく電磁気で磁場中を等速円運動する粒子の項目で扱われてるところだと思われますが，いかがなものでしょうか？

ｙama さんのレス (2006/10/25(Wed) 08:53)

nucleus は中性子ではなく，（原子）核です．（中性子はneutron） 半径 r の球にガウスの法則を適用すれば電場Eが求まるのでτ粒子にはたらく力がわかります． あとはtadashさんが書かれている通り，等速円運動の問題として考えればいいでしょう．