対称テンソルと反対称テンソル
対称テンソルと反対称テンソル
w さんの書込 (2006/10/23(Mon) 18:31)
四元テンソルが
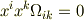
を満たすとき 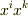 が対称テンソルならば,
が対称テンソルならば, 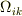 は反対称テンソルであるというのを証明したいのですがわかりません.教科書では自明なこととして扱っているようですが私にはわかりませんでした.教えていただけませんか?
ここで
は反対称テンソルであるというのを証明したいのですがわかりません.教科書では自明なこととして扱っているようですが私にはわかりませんでした.教えていただけませんか?
ここで 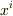 は座標を表します.
は座標を表します.
Re: 対称テンソルと反対称テンソル
toorisugari no Hiro さんのレス (2006/10/23(Mon) 18:45)
ごめんなさい.逆問題をご質問されていたのですね. 以下は無視してください.

となるふたつの量があるとします.このとき
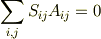
になりますね.
証明
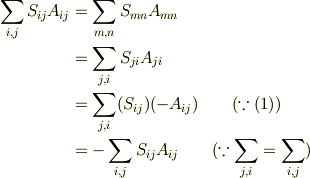
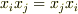 ですからお尋ねの件が成り立つのはおわかりですね.
ですからお尋ねの件が成り立つのはおわかりですね.
Re: 対称テンソルと反対称テンソル
toorisugari no Hiro さんのレス (2006/10/23(Mon) 19:04)
を定数テンソルと考えて
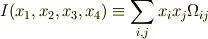
とおき
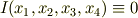
ならば
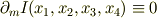
同様に
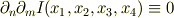
となるのでここから
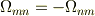
が導けますね.
# 一般の対称テンソルの時の証明はどなたかおねがいします.
(追記)上が成り立つ条件は一般の対称テンソルの場合の必要条件であり, 十分条件はすでに示しているので一般でもなりたちますね.
Re: 対称テンソルと反対称テンソル
MXK さんのレス (2006/10/23(Mon) 20:31)
「 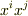 が対称テンソルなら」というところがよく分かりません.
「任意の
が対称テンソルなら」というところがよく分かりません.
「任意の 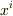 に対して,
に対して, 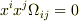 なら」というのなら,以下のようになるのではないでしょうか.
なら」というのなら,以下のようになるのではないでしょうか.
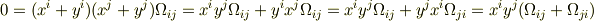
が任意の 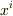 ,
, 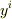 について成り立つので
について成り立つので 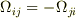 .
.