無題
無題
ZIG さんの書込 (2006/10/17(Tue) 23:34)
微分方程式
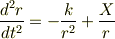
がどうしても解けません 三日ぐらい悩みましたがムリでした. 原点を中心に重力が働く場合の質点の運動を極座標を使ってとこうとしたのですが, 面積速度一定を導いてθを消したところで詰まってしまいました. 解法のヒントなど,いただけたら嬉しいです
Re: 無題
Joh さんのレス (2006/10/18(Wed) 02:19)
kは定数で,Xはtの関数だと思っていいですか?rはtの関数なんですね?他に,何か拘束条件はありますか?
Re: 無題
toorisugari no Hiro さんのレス (2006/10/18(Wed) 11:02)
3次元の万有引力下での惑星運動の問題なら
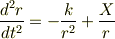
たぶん,右辺第2項が違います.
どのみちこの微分方程式は「私には」とけません.
そもそも何を求めたいのでしょうか. 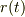 の関数形ですか?
の関数形ですか?
目的や導出までの手順を書いていただければ有用な回答が返ってくると思います.
無題
ZIG さんのレス (2006/10/18(Wed) 19:57)
すみません.指摘の通り右辺第2項が移し間違ってました.
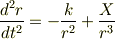
でした. 万有引力のもとで,
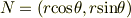
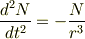
から(ただしθ,rはともに時間の関数)
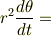
一定
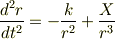
がでてきました.上の式が面積速度一定を表しているらしい事は分るのですが,
下の微分方程式が解けませんでした.
できれば 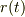 の一般解を出したいのですが
おそらく初頭関数では表現できないかもしれません.
ただ,ある条件の下では,
の一般解を出したいのですが
おそらく初頭関数では表現できないかもしれません.
ただ,ある条件の下では, 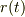 は周期関数になるはずなので
そこから何か分らないかな〜,と.
は周期関数になるはずなので
そこから何か分らないかな〜,と.
中心力の問題
山旅人 さんのレス (2006/10/18(Wed) 23:35)
>> ZIG さん 私の PC では,すぐ上に書かれた5つの式の内,間に挟まれた3式が表示されません.これが見えると,ほんのアドバイス程度のことができるかと思うのですが,再度お書きいただけませんでしょうか.
Re: 中心力の問題
yama さんのレス (2006/10/19(Thu) 09:34)
惑星の運動については,大抵の力学の教科書で説明されているので,図書館などで借りて参考にされるといいと思います.
問題の方程式ですが,形式的にr方向の1次元運動の方程式とみなせば,エネルギーの積分を利用して t を r の関数の積分として表すことができます. 適当な変数変換によって,積分は初等関数で表すことができ,その結果,t と r がその変数をパラメーターとした式で表されることになります. しかし,r を t の関数として表すことは初等関数の範囲ではできないと思います.
Re: 中心力の問題
toorisugari no Hiro さんのレス (2006/10/19(Thu) 20:20)
yamaさんがおっしゃるように力学の教科書を読まれることを勧めます.
> ただ,ある条件の下では,r(t)は周期関数になるはずなので > そこから何か分らないかな〜,と.
そうですね.悪くない考察だと思います.
それなら  を
を  の関数でなく
の関数でなく  の関数と考えた方が良いのでは?
の関数と考えた方が良いのでは?
解きたい微分方程式に 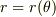 を代入し,
を代入し,  微分をライプニッツ則で
微分をライプニッツ則で  微分に変換し,後は非線形方程式の解法の常道で
微分に変換し,後は非線形方程式の解法の常道で
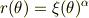
と変数変換して,式が簡単になるような定数  を探せば解けると思いますよ.
を探せば解けると思いますよ.
Re: 中心力の問題
山旅人 さんのレス (2006/10/19(Thu) 21:39)
私は,『現代物理学を学ぶための 古典力学』(伏見康治・著 岩波)をお勧めします.お近くの図書館で是非ご覧下さい.
この本は,私は名著と信じるものですが,残念ながら絶版で,もはや手に入りません. 本レスをご覧の皆様,是非「復刊」投票にご協力下さい.
100票で復刊検討にはいるそうです.まだ道のりは長〜い,のですが…
無題
ZIG さんのレス (2006/10/20(Fri) 20:21)
返信有難う御座います. こんど図書館にいったとき探してみます.
上の表示されていなかった部分は修正しました. PCの問題ではなく私の書き方が間違ってました. Latexはまだ不慣れなもので(^^A
tからθへの変数返還,試して見ます