熱力学

home > 掲示板 >

このページのPDF版

サイトマップ

熱力学

カリプソさんの書込 (2006/10/17(Tue) 22:01)

お久しぶりです．大学の授業で課せられた宿題なのですが，質問させてください．

van der Waalsの式は（Ｐ＋a/V^2)(V-b)=nRTとあらわされる．このとき

熱膨張係数：α＝1/V(∂Ｖ／∂Ｔ）圧縮率：ｋ＝−１/V(∂V/∂P) を求めよ．

です．理想気体のときのようにＶを求めてそれぞれ代入して計算しようと思ったのですがうまくいきませんでした．どなたかどうやったらよいのか教えてください．

Re: 熱力学

のぼりんさんのレス (2006/10/17(Tue) 23:14)

こんばんは．偏微分の数学問題と考えれば，以下の様に計算できますが，頓珍漢かも知れません．その節はご容赦下さい．

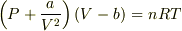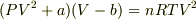$\left(P + \frac{a}{V^2}\right) \left(V - b\right) = nRT$ を (P V^2 + a)(V - b) = n R T V^2 と書き直し，P と T を独立変数とみなして両辺を T で偏微分すれば，

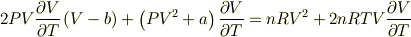
$2 P V \frac{\partial V}{\partial T} \left(V - b \right) + \left(P V^2 + a \right) \frac{\partial V}{\partial T} = n R V^2 + 2 n R T V \frac{\partial V}{\partial T}$

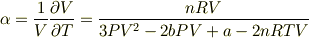
$\alpha = \frac{1}{V}\frac{\partial V}{\partial T} = \frac{n R V} {3 P V^2 - 2 b P V + a - 2 n R T V}$

です．同様に，両辺を P で偏微分し 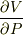$\frac{\partial V}{\partial P}$ についてまとめれば，も求められます．

Re: 熱力学

カリプソさんのレス (2006/10/17(Tue) 23:40)

ご解答ありがとうございます．αを求めるときはＰを，kを求めるときはＴを固定する偏微分の問題だと思うのですが，答えとしてはＶという文字が残ってもよろしいのでしょうか？

Re: 熱力学

のぼりんさんのレス (2006/10/18(Wed) 20:59)

こんばんは．

＞αを求めるときはＰを，kを求めるときはＴを固定する偏微分の問題だと思うのですが， No.12297 はその積りで返信しましたので，ご安心下さい．

＞答えとしてはＶという文字が残ってもよろしいのでしょうか？質問の出所も趣旨もわからない以上，これに関しては当方ではわかりかねます．恐縮ですが，カリプソさんご自身で判断下さい．

仮に，式からＶを完全に消去し，ＰとＴのみで表示するのが題意だとすれば，三次方程式 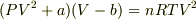(P V^2 + a)(V - b) = n R T V^2 をカルダノの方法で解き，先に得られた α の式に代入すれば，原理的には解くことができます．ただし，実際にやっていませんが，この解は相当に複雑になると思われます．正直，私の計算力では，正確な計算をする自信がありません．

Re: 熱力学

カリプソさんのレス (2006/10/19(Thu) 00:45)

返信ありがとうございます．

∂Ｖ/∂ＴというのはＶはＴの関数として表されるということで，Ｖを消去してＴで表すべきなのかな〜という程度の疑問です．題意とかで指定されているわけではなくふと疑問に思っただけでした．表記としては別に問題ないということですね？

それと今更ではありますが，van der waalsの式は，（p＋an^2/V^2)(V-nb)=nRT の間違いでした．すみません．

Re: 熱力学

サボテンさんのレス (2006/10/19(Thu) 19:55)

横から失礼いたします．物理の問題としてものぼりんさんの回答で問題ないと思います．熱膨張係数は，無理にTであらわす必要はないと思います．

Re: 熱力学

のぼりんさんのレス (2006/10/19(Thu) 21:57)

こんばんは．

サボテンさん，別掲示板ではお世話になっています．また補足いただき，感謝致します．

＞表記としては別に問題ないということですね？サボテンさんが既に回答下さいましたが，たとえば 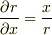$\frac{\partial r}{\partial x} = \frac{x}{r}$ と表記するのを見てもお分かりの様に，偏微分する関数を計算結果に入れてはいけない，というルールは，一般的にはないと思います．ただしつこい様ですが，本問固有の条件等により，被微分関数を消去しなければならない可能性も十分にありますから，その当たりはカリプソさんご自身で判断いただければと思います．

Re: 熱力学

カリプソさんのレス (2006/10/20(Fri) 02:26)

のぼりんさん，サボテンさん，ありがとうございました．助かりました．また質問することがあると思いますがその時はまた宜しくお願い致します．

[home] [掲示板] [ページの先頭]