電磁気学の積分

blue さんの書込 (2006/10/15(Sun) 14:54)

ｙ軸-ｂからaに一様に分布した電荷λ[C/m]のｘ軸上の点の電位を求める問題で， V=λ/4πε∫[-b→a]dy/(r^2+y^2)^(1/2)で ∫[-b→a]dy/(r^2+y^2)^(1/2) の定積分の前の不定積分ができなくて困っています．どなたかご教授ください．

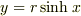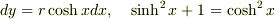こんにちは，blue さん．この手の数学問題であれば，私でもお手伝いできそうです． $y = r \sinh x$ とおけば， $dy = r \cosh x dx, \quad \sinh^2 x + 1 = \cosh^2 x$ なので，

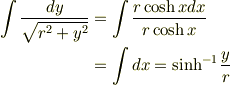
$\int \frac{dy}{\sqrt{r^2 + y^2}} &= \int \frac{r \cosh x dx}{r \cosh x}\\ &= \int dx = \sinh^{-1} \frac{y}{r}$

です．ここで，

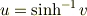
$u = \sinh^{-1} v$

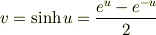
$v &= \sinh u = \frac{e^{u} - e^{-u}}{2}$

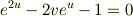
$e^{2u} - 2 v e^{u} - 1 = 0$

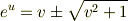
$e^{u} = v \pm \sqrt{v^2 + 1}$

です．複号で − を取ると負になってしまうので＋を採用し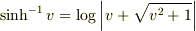， $\sinh^{-1} v = \log \left| v + \sqrt{v^2 + 1} \right|$ です．これを使えば，双曲正弦の逆関数を対数関数で書き表せます．

のぼりんさん，ありがとうございます．参考にさせていただきます．