電磁波の放射

home > 掲示板 >

このページのPDF版

サイトマップ

電磁波の放射

のぼりんさんの書込 (2006/10/09(Mon) 20:26)

こんばんは．テスト用掲示板の件では，大変お世話になりました．さて今，電磁気の復習で，川村「電磁気学」（岩波） 172 ページの演習問題３に取り組んでいます．

本文中では，電磁波の源と観測点との距離が波長に較べて十分長く，平面波で近似できる場合を考えた．電流や電荷が分布している領域のサイズに較べれば十分遠いが，波長と較べると短い距離で観測するときの電場ベクトルを 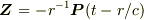$\bm{Z}=-r^{-1}\bm{P}(t-r/c)$ で定義される 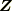$\bm{Z}$ を使って表せ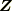（ $\bm{Z}$ をヘルツのポテンシャルとよぶ）．

この略解は，以下のとおりです．

(7.54) の次の 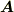$\bm{A}$ の表式

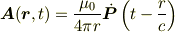
$\bm{A}(\bm{r},t)=\frac{\mu_{0}}{4\pi r}\dot{\bm{P}}\left(t-\frac{r}{c}\right)$

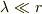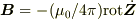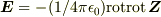は，この問題でも正しい．しかし (7.55) 以下は (7.46) 〔 $\lambda \ll r$ 〕を使っているから，いまは使ってはならない． $\bm{B}=-(\mu_{0}/4\pi)\mathrm{rot} \dot{\bm{Z}}$ ， $\bm{E}=-(1/4\pi \epsilon_{0})\mathrm{rot rot} \bm{Z}$ ．

領域のサイズが観測点との距離と比べて十分小さいことから，ローレンツ・ゲージで

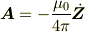
$\bm{A}=-\frac{\mu_{0}}{4\pi}\dot{\bm{Z}}$

と書け，従って，磁場が表式で表せるところまでは判るのですが，電場の式をどう導くのかわかりません．電場の導出過程をご教示願えますか．何卒よろしくお願い致します．

Re: 電磁波の放射

山旅人さんのレス (2006/10/09(Mon) 22:29)

のぼりんさん，こんばんは．私の手許にある『場の古典論』には，次のように書かれています．ただし，単位系の違いで係数が異なっています．その差異は，のぼりんさんが埋めてください．

−−−−−− <b>A</b>＝(1/c)(∂/∂t)(<b>P</b>/r) …(1) ローレンツゲージ div<b>A</b>＋(1/c)(∂φ/∂t)＝0 …(2)

(1)を(2)に代入し，時間について積分すると， φ＝−div(<b>P</b>/r) …(3) <b>E</b>＝graddiv(<b>P</b>/r)−(1/c ² )(∂ ² /∂t ² )(<b>P</b>/r) …(4)

<b>P</b>/r がダランベールの方程式(1/c ² )(∂ ² /∂t ² )(<b>P</b>/r)＝Δ(<b>P</b>/r)を満たすことに注意すれば，ベクトル解析の公式から， <b>E</b>＝rotrot(<b>P</b>/r) …(5)

<b>Z</b>＝−(1/r)<b>P</b>(t−r/c)(ヘルツベクトル) とおくと， <b>E</b>＝−rotrot(<b>Z</b>) …(6) −−−−−−−−−−−

式の番号は，もちろん原文とは異なります． (6)は，のぼりんさんがお書きのものとあっているようですね．

Re: 電磁波の放射

のぼりんさんのレス (2006/10/09(Mon) 22:55)

山旅人さん早速の返信，どうもありがとうございました！物理は独学のため自分で解決する力に乏しく，困っていたところでした．ご教示本当に助かりました．(^^)

[home] [掲示板] [ページの先頭]