静止摩擦力

静止摩擦力

ヤマハ さんの書込 (2006/09/24(Sun) 12:33)

物理の摩擦力の問題で詰まってしまって，どなたかご回答願います．

１２０ｍの半径，傾斜のあるカーブをスピードが20m/sであれば向心力でまわれる． （静止摩擦力が発生していない状態），もしこのカーブを30m/sのスピードで 走ったときの静止摩擦係数はいくつですか？ という質問です．

20m/ｓのときの傾斜を18.78度というところまでときました． その後は，Fx=ｎsin（18.78)＋ｎ摩擦係数cos（18.78)=m（ｖ2乗/ｒ） の計算でとけばいいのでしょうか？

よろしくお願いします．

Re: 静止摩擦力

Joh さんのレス (2006/09/24(Sun) 18:08)

ヤマハさん，こんにちは．

まず，私は向心力でまわれる，という意味がよく分かりません． 向心力を発生しているのですか？それとも，道路にバンク角が ついていて，重力と遠心力が釣り合うという意味でしょうか？

もう一点，運動している状態で，静止摩擦係数を求めるという 意味がよく分かりません．問題はこれで全文ですか？？

分からないことだらけですみません．

Re: 静止摩擦力

ヤマハ さんのレス (2006/09/25(Mon) 01:02)

読んでいただいてありがとうございます．

まず，私は向心力でまわれる，という意味がよく分かりません． 向心力を発生しているのですか？それとも，道路にバンク角が ついていて，重力と遠心力が釣り合うという意味でしょうか？

はい，バンク角がありそのとおりです．

同じ条件のカーブをスピードを変えて走る場合の 最小静止摩擦係数をしりたいのです．問題は静止摩擦係数といってます．

アクセレーションのみを2.25倍にすればいいのでしょうか？

Re: 静止摩擦力

Joh さんのレス (2006/09/25(Mon) 06:06)

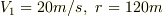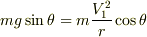最初の状態で，遠心力と重力がちょうど釣り合うということは， V_{1}=20 m/s, \ r=120m として， mg\sin \theta = m\frac{V_{1}^{2}}{r}\cos \theta がなりたつということですよね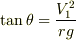． \tan \theta = \frac{V_{1}^{2}}{rg} です．

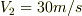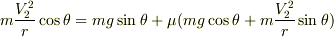増速すると，遠心力が大きくなるので，釣り合うように摩擦が働くんだと思うんですが，半径方向の力の釣り合いの式は V_{2}=30m/s として， m\frac{V_{2}^{2}}{r}\cos \theta = mg\sin \theta + \mu (mg \cos \theta + m\frac{V_{2}^{2}}{r}\sin \theta ) となるでしょうか．これを解くと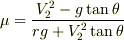， \mu = \frac{V_{2}^{2}-g\tan \theta}{rg+V_{2}^{2}\tan \theta} となるように思います．あとは数値を代入するだけです．計算間違いしてないといいんですが．．．．

Re: 静止摩擦力

ヤマハ さんのレス (2006/09/25(Mon) 11:05)

回答ありがとうございました． いただいた数式で計算してみます．

Re: 静止摩擦力

ヤマハ さんのレス (2006/10/05(Thu) 22:22)

はい，そうでした．

ありがとう

Re: 静止摩擦力

山旅人 さんのレス (2006/10/09(Mon) 09:54)

この問題が，ずっと気になっていました． ヤマハさん，お手数ですが，問題文の原文を（記号の定義を含めて）書いていただけませんか．