中間テストの過去問?
中間テストの過去問?
Chippy さんの書込 (2006/09/24(Sun) 10:49)
電場と電位に関連した, ラザフォードについての中間考査の過去問です.この問題は模範解答はありません.
ラザフォード はbegan to study the internal structure of the atom by shooting the α particles at it. In a 1911 paper called The Scattering of α and β Particles by Matter and the Structure of the Atom,
ラザフォード says: “In order to form some idea of the forces required to deflect(そらす/偏向) an (α) particle through a large angle, consider an atom [as] containing a point positive charge (Ne) at its centre, and surrounded by a distribution of negative electricity −(Ne) uniformly distributed withina sphere of radius (R). The electric field (E) and the potential (V) at a distance (r) from the centre for a point inside the atom, are given by
E =(Ne)/(4πε){ [1/(r^2)] - [r/(R^3)]}
V = (Ne)/(4πε){ (1/r)-(3/2R) + [(r^2)/(2R^3)]}
- Derive Rutherford’s formula for E. (10 points)
(b) Using the formula for the electric field, and assuming that the electric potential is zero at r = R,derive Rutherford’s formula for the electric potential V as a function of r inside the atom. (10points) ヒント: Choose the path of integration starting at an arbitrary point r straight out to the radius R so that the electric field will be in the same direction as the path of integration.
ガウスの法則q=ε∫E・dA 電位はV =∫E・ds
半径がQの急の内側に閉曲面(中心から半径r)を考え解くのだと思うのですが. (q_enc)=ε∫[0→4πr^2](E)(dA) =ε(E)4πr^2 ここまでは判るのですが,これからがどのように進めて行けば,2つの公式に辿り着くかが判りません.
ご指導をお願いいたします.
Re: 中間テストの過去問?
mNeji さんのレス (2006/09/25(Mon) 15:08)
どなたからの回答がないようなので,ヒントだけ書きます.それで,判らなければ他の方法を考えます.
【ヒント】 1) 原子核は電荷+eをN個もつ点電荷, +Neと考える. 2) N個の電子は,半径Rの球(中心は原子核に一致すると近似)に
均一に分布していると仮定.この場合の取り扱いは, 以前,yamaさんに習われた筈だとおもいます.
- 電磁気のばあい,電荷や磁気双極子の作る場は線形なので,
別々に考えて,足し合わせることが出来ます. この問題で言えば,E,Vの第一項は1)の原子核の作り出す 電場と,静電ポテンシャルです.残りの項が均一電子雲が作る部分と思います.電荷密度はですね.
- こう考えると,細かく解く前に;
- [a]r>=Rでは,原子核の作るクーロン場と
- 電子が作るクーロン場はお互いにキャンセルしてゼロ.
- [b]r→0では,電子雲がつくるクーロン場は消失して,
- 原子核の作るクーロン場に漸近する.
と推測できます.
====
前回の時計の文字盤の問題といい,この問題といい,これまで拝見した問題を総合すると,Chippyさんの先生は, 物理のセンスがよい方のような気がしてきました.
#少なくとも,良く練った問題で,細かな数学的アクロバットを求めて無いですね. #日本の高校の物理の問題が学ぶべきと思うぐらいです.
私は,Chippyさんとは無縁の問題で,こちらのサイトに書くことを辞めました.他の回答者の方々に揉んでいただいて「もう少し物理数学」の力をつければ「Chippyさんの先生も,丁寧に教えてくれるようになる」と思います.その前哨戦と考えて,これからのテストを頑張ってください.
どうしても,判らんというところがあれば,メイル先を書いてください.1回だけは付き合います.
Re: 中間テストの過去問?
Chippy さんのレス (2006/09/25(Mon) 22:58)
mNejiさん,いつもご丁寧な解説をしていただきまして本当に感謝しております.
(q_2)=ε∫[0→4πr^2](E)(dA)
-Ne=ε(4πr^2)(E) E=(-Ne)/(q4πr^2)
E_total=Ne−(Ne/4πεr^2)
電荷密度はρは 以前yamaさんにご指導いただきました.Q/V=q/vより (-Ne)/[(4/3)επR^2]=Ne/([(4/3)επr^2) と解いたと考えてよろしいですか?
そして,これらから E =(Ne)/(4πε){ [1/(r^2)] - [r/(R^3)]}に到達するにはまだ何か足らないものがあると思いますが,どうやたら搾り出せますでしょうか・・・.
また,ρはガウスの∫式にどのように組み込んで計算すればよいですか?
mNejiさんの解答ををこれから頂けなると考えると,とても心細く感じます.諸事情のためなら仕方ありませんね.もしよかったら,メールアドレスを交換したいものなんですが.
いつも本当にありがとうございます.
Re: 中間テストの過去問?
mNeji さんのレス (2006/09/25(Mon) 23:31)
今後の連絡に付いては,この数式掲示板の管理をされているCOさんに相談してみてください.
COさんがChippyさんの特殊事情をどう理解されるかによると思います.COさんに連絡をするにはCOさんが回答されているページの先頭に「CO@物理のかぎプロジェクト」みたいな所の「CO」をクリックするとアドレスがかいてあるページにリンクすると思います.
Re: 中間テストの過去問?
mNeji さんのレス (2006/09/26(Tue) 00:58)
途中まで書いて,その後,メイルにしてしまうと; 1) 他の人で見ていた方にアンフェア, 2) 試験まじかで,交渉の余裕が少ない
と思われますので,要点だけを書いてみます.
静電場のガウスの法則(積分形),
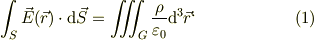
から出発します.
ここで,座標の原点に考える原子の「原子核(電荷+Ne)」があり,それを中心に半径Rの球の内部に均一な電子の雲(総電荷-Ne)があると近似する.
重要な仮定は,電荷分布が球対称なことです.その為,クーロンの法則からも容易に予想できるように,電場も球対称で,原点からその位置までの位置ベクトルの指す方向に電場があること.

式(1)の曲面  は閉曲面ならなんでもいい訳ですが,座標原点から,半径rの球表面とします.すると,微小面積ベクトルも,常に位置ベクトルの指す方向に向いている:
は閉曲面ならなんでもいい訳ですが,座標原点から,半径rの球表面とします.すると,微小面積ベクトルも,常に位置ベクトルの指す方向に向いている:
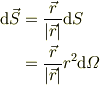
ここで, 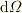 原点から
原点から  を見込む立体角.
を見込む立体角.
従って,式(1)左辺は
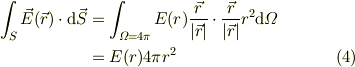
他方,式(1)右辺の積分の意味は,領域`G`に含まれる電荷の総和を意味するのだから,原子核に電荷は何時も,総和に含まれる事に注意する:
電子雲の電荷密度, 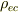 は,
は,
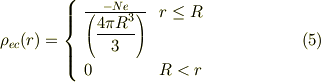
これらから,電荷の体積分は;
![\int\mspace{-11mu}\int\mspace{-11mu}\int_{G}\rho(r')\mbox{d}^3\vec r'&= +Ne +\int\mspace{-11mu}\int\mspace{-11mu}\int_{G}\rho_{ec}(r')\mbox{d}^3\vec r'\\&= +Ne + \int_{r'=0}^{r'=r}\int_{\varOmega=4\pi} \rho_{ec}(r')r'^{2}\mbox{d}r'\mbox{d}\varOmega \\&= +Ne + 4\pi\int_{r'=0}^{r'=r}\rho_{ec}(r')r'^{2}\mbox{d}r'\\&= +Ne + 4\pi\rho_{ec}\left\{ \begin{array}{l c}\int_{r'=0}^{r'=r}(r')r'^{2}\mbox{d}r' & r \le R \\\int_{r'=0}^{r'=R}(r')r'^{2}\mbox{d}r' & R < r \end{array}\right. \\&= \left\{ \begin{array}{l c}+Ne[1-(r/R)^3], & r \le R \\0, & R <r\end{array}\right. \tag{6}](http://hooktail.maxwell.jp/bbslog/96d027716042bf8b33ab5d00123b1cf1.png)
式(1)に式(4)と式(6)を代入して,ガウスの静電荷の式・積分形として,
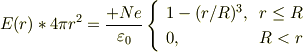
電場の成分 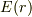 は;
は;
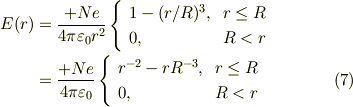
電場の成分は,Rの外側では,原子核のクーロン場は電子雲のクーロン場に遮蔽されて(打ち消されて)ゼロになってしまう.他方Rより内側に入っていくと,電子雲の遮蔽は線形に減少し,rが小さくなると原子核のクーロン力に漸近する.
静電ポテンシャル 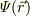 を天下り的に定義すると,電場と微小変位との内積を無限遠方から位置
を天下り的に定義すると,電場と微小変位との内積を無限遠方から位置 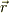 まで総和し,その符号を変えたものに等しい.しかし,球対称であることから,式(2)のような性質を利用して,積分を簡潔にできる.なお,積分の式に出てくる位置ベクトルのパラメータを
まで総和し,その符号を変えたものに等しい.しかし,球対称であることから,式(2)のような性質を利用して,積分を簡潔にできる.なお,積分の式に出てくる位置ベクトルのパラメータを 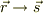 とした.また
とした.また 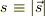 とした.
とした.
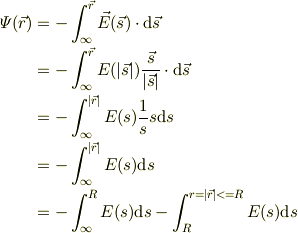
ここで,式(7)を考慮すると,右辺の第一項は消えるから,
![\varPsi(\vec r) &= -\int_{R}^{r=|\vec r|<=R}E(s)\mbox{d}s\\&=-\int_{R}^{r=|\vec r|<=R}\frac{+Ne}{4\pi \varepsilon_{0}}(s^{-2}-sR^{-3}) \mbox{d}s\\&=-\frac{+Ne}{4\pi \varepsilon_{0}}\int_{R}^{r=|\vec r|<=R}(s^{-2}-sR^{-3}) \mbox{d}s\\&=-\frac{+Ne}{4\pi \varepsilon_{0}}[-s^{-1}-\frac{s^{+2}}{2R^{+3}}]_{s=R}^{s=r}\\&=\frac{+Ne}{4\pi \varepsilon_{0}}[s^{-1}+\frac{s^{+2}}{2R^{+3}}]_{s=R}^{s=r}\\&=\frac{+Ne}{4\pi \varepsilon_{0}}[r^{-1}-R^{-1} +\frac{r^{+2}}{2R^{+3}}-\frac{R^{+2}}{2R^{+3}}]\\&=\frac{+Ne}{4\pi \varepsilon_{0}}\left( r^{-1} +\frac{r^{+2}}{2R^{+3}}-\frac{3}{2R}\right) \tag{8}](http://hooktail.maxwell.jp/bbslog/a29f47e2c9dfb6c8466c94cfcc67c4c6.png)
以上.
=====
●おまけ● 静電ポテンシャルから電場を出したい時.
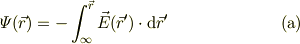
ポテンシャルの傾きが場の方向を示すわけですから,ポテンシャルの微分を考えます:
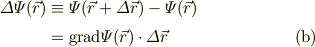
今度は,式{a}を用いると;
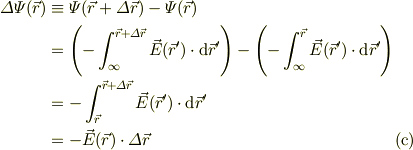
式(b),(c)を比較して,
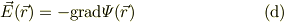
おまけの終り.
Re: 中間テストの過去問?
mNeji さんのレス (2006/09/26(Tue) 19:25)
● 球対称な電荷分布のまとめ ●
計算が長くなったので,別枠で考え方を見直して見ます.
静電場のガウスの法則(積分形)は,対象が持つ幾何学的特長に強く依存した,ある意味では,特殊な計算手法であることがお分かりになったと思います.今回の場合は球対称性を利用したわけですが,無限の平面だとか,同軸の面だとかケースによって違いますが,考え方だけはどれも似たりよっやりですから,その時でも,球対称との違いに注意すれば,すぐに慣れますね.
ということで,● 球対称電荷 ● をおさらいすると,
● 電場も動径方向成分だけ ● <---> 中心力! 重力も一緒.

これによって,ガウスの静電荷の法則(積分形)がとてもコンパクトな式;
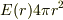 = (半径rに含まれる電荷/
= (半径rに含まれる電荷/ 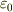
になってしまう訳です.
で,一番手間取るのが「電荷分布を半径の関数として出すこと」だったのがお分かりでしょう.
● 静電ポテンシャルも半径だけの関数 ●
私は,具体的計算に不慣れなので,一般論から説明しました.他方,Chippyさんの先生は,生徒さんたちがベクトル解析がまだなので,一次元問題として説明されているのだろうと,今頃になって気づきました.その意味では,電場が出れば,その線積分でポテンシャルがでると考えれば,下記の式がすぐに出るわけですね.
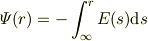
● 終りに ●
こうやって,かなりの問題を解いているうちに,Chippyさんの先生は,物理をかなり深く理解されている方のように感じてきました.
初めのうちの印象は,教師になりたての若い方のように感じましたが,最近は逆にかなりお年を召された方では無いかと思うようになりました.
恐らく,この方は,「ちょっと捻った問題を作るのが得意」なので,「一寸,工夫した回答」を出すと感激してBをAにするようなタイプと思います.
為には,物理数学をガッチリとガードして望めば,仲良くなれるような気がします.その為にも,この数式掲示板の回答者の皆さんに揉んでもらいましょう.
一先ずは,アデュー.
Re: 中間テストの過去問?
Chippy さんのレス (2006/09/26(Tue) 20:41)
mNejiさん,本当に詳しい解説いただきまして本当にありがとうございます.
計算課程の解説ありがとうございます.
英語の物理を敬遠しがちでしたが球対称な電荷分布,電場の動径方向成分, 静電ポテンシャルの解説をこうして日本語で説明を受けますと,親しみを感じてきました. この問題と同じ様な類題も,解説のおかげで何とか解けるようになりました.mNejiさん,他皆様にとても感謝しております.明日(現地時間)テストがありますので,今日一日もう一回じっくり復習していきたいと思います.
追記:私の教授は30歳前後の白人の方です.
Re: 中間テストの過去問?
mNeji さんのレス (2006/09/26(Tue) 22:45)
>明日(現地時間)テストがありますので,今日一日もう一回じっくり復習していきたいと思います.
ベストを尽くされてください.
>The Scattering of α and β Particles by Matter and the Structure of the Atom,
ラザフォードさんのα線(He原子:ウランなどのα崩壊から)を用いた散乱実験は教科書にでて有名ですがβ線(電子)の散乱は知りませんでした.電子は標的原子(恐らく金の薄膜)の電子雲から強い反発を受け,質量も少ないし,多体電子と電子の散乱なので挙動がふくざつだとおもいます.
何かの機会に,β線を実際に実験に用いたか質問すると面白い話が聞けるかもしれません.
では,どこかで.