Chippy さんの書込 (2006/09/18(Mon) 16:47)

A charge Q1 = 1.43 μC is at rest and is located 2.10 cm away from another fixed charge Q2 = 1.75 μC. The first charge is then released. Calculate the kinetic energy of charge Q1 when it is 4.60 cm away from charge Q2.

教科書の公式を基に解きますと． ΔＫ＝Ｗ(app) ＋Ｗ

Ｗ(app)＝(q)(ΔＶ）

ΔＶ＝∫[initial→final]Ｅ・ｄｓ ΔＶ＝∫[0.021→0.046]Ｅ・ｄｓ

Ｗ(app)＝(q)ΔＶ＝(q)Ｅ(0.046-0.021)

Ｗ＝（q_0）∫[initial→final]Ｅ・ｄｓ ，(q_0)は fixed chargeです Ｗ＝（1.75 μ）∫[0.021→0.046]Ｅ・ｄｓ

ΔＫ＝｛（1.43 μC）Ｅ(0.025)｝＋｛（1.75 μ）Ｅ(0.025)｝

Eはクーロンの法則より E＝｛ｋ(1.75 μC)(1.43 μC）｝/（0.046-0.021)^2

この問題はこのような考え方でよろしいでしょうか？ほかに近道など有りましたら教えてください，よろしくお願いします．

yama さんのレス (2006/09/18(Mon) 17:44)

q_0 と q は問題文に合わせて Q1，Q2 と書くべきでしょう．

Q2 は動かないのでその運動を考える必要はありません． Q2 がつくる電場からの力で Q1 が加速されると考えます． Q1 は初めは静止しているので，電場のした仕事がそのままQ1の運動エネルギーになります． 従って ΔＫ＝Ｗ(app) ＋Ｗ ではなく Ｋ＝Ｗ＝∫[initial→final]Q1Ｅ・ｄｓ です． また，E＝｛ｋ(1.75 μC)(1.43 μC）｝/（0.046-0.021)^2 ではなく Ｅ＝kQ2/(s^2) です． これにQ1を掛けたものを ｓ＝0.021 から ｓ＝0.046 まで積分するわけです．

なお，電位 Ｖ＝−∫Ｅ・ｄｓを用いると Ｗ＝−Q1(Ｖfinal−Ｖinitial)＝Q1(Ｖinitial−Ｖfinal) と表すこともできます．

mNeji さんのレス (2006/09/18(Mon) 18:20)

前の問題もそうですが，運動方程式を積分することで，問題を解くことは出来ます．

上に書かれたのはそういうことと推察します．

他の方法といっても，似たり寄ったりなのですすが，運動方程式を積分した結果を，静電ポテンシャルとして使うのも簡単です．

いま原点に，固定電荷Qがあるときに，そこから位置 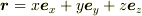の場所の静電ポテンシャル 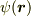は，

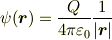
となります．

固定電荷の位置以外の適当なところに原点を置いて，動く電荷qの運動を考えてりと，最初の位置 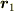での運動エネルギー 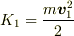とし動いた先の位置や運動エネルギを添え字2で表せば，エネルギー保存の式として；

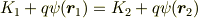
が成立することを用います．

初めに粒子が静止していれば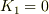， ですよね．

またポテンシャルや電場には，誘電率を忘れずに．

私は，昔自分が勉強につかった電磁気の本の著者の砂川 重信さんが大学で電磁気を学ぶ初心者むけにお書きになった「電磁気の考え方」，岩波書店，ISBN4-00-007892-5という本を買って見ました．比較的噛み砕いて書いてあるので，予備教材とすると良いかもしれません．

ご覧の方で，よりよい教材をご存知でしたら，お教えくださると助かります．

Ｃｈｉｐｐｙ　　 さんのレス (2006/09/19(Tue) 08:36)

yamaさん，ｍNejiさん，アドバイス有難うございます．

Ｅ＝kQ2/(s^2)＝(9×10^9)(Q2)/(0.046)^2＝7443289N/Cとなり （この場合のｓは(Ｑ_1)の最終到着点の0.046ｍを取りました）

Ｋ＝Ｗ＝∫[initial→final]Q1Ｅ・ｄｓ Ｋ＝(1.43 μ）∫[0.021→0.046] (7443289)(ds)＝0.2661となりました．

ｙama さんのレス (2006/09/19(Tue) 09:15)

それでは積分を計算したことにはなりません． 定積分を計算するには，まず不定積分を計算して原始関数F(s)を求めてから，F(0.046)-F(0.021) を計算しないといけません．

Chippy さんのレス (2006/09/19(Tue) 12:45)

ありがとうございます

F＝ｋ（q_1）(q_2)/r^2のｒの値は移動する前と，移動後どちらの値を Ｋ＝Ｗ＝∫[initial→final]Q1Ｅ・ｄｓのF(s）の為に使えばいいのでしょうか？

ｙama さんのレス (2006/09/19(Tue) 13:37)

ちょっと誤解があるようですが，F(s) と書いたのは原始関数で，力ではありません． 結局，次の積分を計算するわけです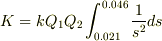． はじめから被積分関数にsの値を入れるのではなく，sのままで不定積分を計算し，その後s=0.046を代入した値からs=0.021を代入した値を引くわけです．