電位　?

Chippy さんの書込 (2006/09/18(Mon) 16:23)

電位の分野で，でてきた問題なのですが電位[V]や仕事量[W]も与えられておりません．

問題 A positive charge of 4.30μC is fixed in place. From a distance of 3.00 cm a particle of mass 5.50 g and charge +3.10 μC is fired with an initial speed of 80.0 m/s directly toward the fixed charge. How close to the fixed charge does the particle get before it comes to rest and starts traveling away?

固定電荷Aは＋4.30μC が5.50 g のB電荷 +3.10 μC から３ｃｍ離れており，次に電荷 +3.10 μCは80ｍ/ｓで固定電荷へ向け放たれた．BはどれだけAに接近すれば一時的に静止するか？

位置，質量と速度の値がわかっていますがこれらをどのように活用すれば良いか良かったら教えてください．

Re: 電位　?

mNeji さんのレス (2006/09/18(Mon) 17:40)

運動して帰ったばかりなので，指が思うように動かないので，ヒントだけ．

粒子に対する抵抗は無視するのでしょうから，「運動エネルギー＋静電エネルギーの和が一定」を使えばどうですか？

Re: 電位　?

Ｃｈｉｐｐｙ　　さんのレス (2006/09/19(Tue) 09:04)

有難うございます．

先に教えていただきました (Ｋ_1)＋｛ｋ×(Ｑ/ｒ_1)＝(Ｋ_2)＋｛ｋ×(Ｑ/ｒ_2)より

｛ｍ(ｖ^2)/２｝＋｛ｋ×（4.30μC)/(0.03ｍ)＝０＋｛ｋ×(4.30μC)/（r_2)

Ｋ＝(0.0055)(80^2)/２＝17.6

17.6＋1290000＝０＋(38700/r_2)

（r_２）＝2.99×(10^-2)ｍとなりました．

Re: 電位　?

mNeji さんのレス (2006/09/19(Tue) 14:16)

途中まではあっていますが，Q_Bが忘れられているかなどの為に間違えているようです．

全エネルギー保存の式から書いてみると；

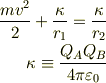
$\frac{mv^2}{2}+\frac{\kappa}{r_1}=\frac{\kappa}{r_2} \\\kappa \equiv \frac{Q_{A}Q_{B}}{4\pi \varepsilon_{0}}$

求める値は；

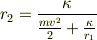
$r_2 =\frac{\kappa}{\frac{mv^2}{2} + \frac{\kappa}{r_1} }$

で与えられる．

ここで；

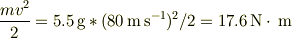
$\frac{mv^2}{2}=5.5\unit{g}*(80\unit{m}\unit{s^{-1}})^{2}/2=17.6\unit{N}\cdot\unit{m}$

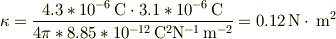
$\kappa = \frac{4.3*10^{-6}\unit{C}\cdot 3.1*10^{-6}\unit{C}}{4\pi* 8.85*10^{-12}\unit{C^{2}N^{-1}}\unit{m^{-2}}}=0.12\unit{N}\cdot\unit{m^{2}}$

よって

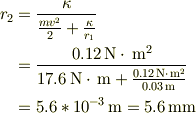
$r_2 &=\frac{\kappa}{\frac{mv^2}{2} + \frac{\kappa}{r_1}} \\&=\frac{0.12\unit{N}\cdot\unit{m^{2}}}{17.6\unit{N}\cdot\unit{m} + \frac{0.12\unit{N}\cdot\unit{m^{2}}}{0.03\unit{m}}} \\&=5.6*10^{-3}\unit{m}=5.6\unit{mm}$

Re: 電位　?

mNeji さんのレス (2006/09/21(Thu) 14:13)

Chippyさん：

諸般の事情で，私の回答は明日までとすることになりました．

これまでに，静電気に関する質問が多かったと思うので，静電気の問題の根底にある運動方程式から静電場を見るとどういうことかを説明してみました．

＃静電ポテンシャルを，いつもいつも積分から考えなくてもいいのです．＃ベクトル解析がまだでしたら，将来見直されるのも良いですよ．

普通，このような説明は，もっと一般的な中心力などの説明で出てくるとおもいますが，今回のように逆自乗の力の場；クーロン力に絞って眺めるのも，一興かとかんがえました．なお，逆自乗の力の場としては，重力の場も同じ性質をお持つことを申し添えておきます．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

真空中に於ける現象とします．固定粒子；電荷Q,質量W；が座標原点にあり，そこから位置 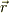$\vec r$ に位置する運動可能な粒子；電荷q，質量w；の運動について考えます．すこし簡略かしていますが，典型的な問題なので，考え方を整理しておきましょう．

運動方程式は；

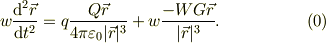
$w\frac{\mathrm{d}^2 \vec r}{\mathrm{d} t^2} = q\frac{Q \vec r}{4\pi\varepsilon_{0} |\vec r|^{3}}+w\frac{-WG\vec r}{|\vec r|^{3}}. \tag{0}$

この式は運動粒子の加速度は，外力の総和によって決まることを示しています．右辺第一項はクーロン力，第二項は重力によるものです．

ご存知のように，地球と月のように大きな質量同士でないと重力は強く働きません

＃いちさんのご指摘により，下記の＃ (言い換えれば重力は弱い相互作用とも言われます)．＃発言を削除いたします．記：2006-09-30, ｍNeji.

そしてこのような大きいサイズの物体には大きな電荷が存在しません．仮にそのような電荷の偏りが存在すれば，加速される荷電粒子は電磁波のエネルギーを放出するため[注1]に安定的な公転運動を維持できなくなるのです．

[注1] 荷電粒子の運動による電磁場 [物理のかぎしっぽ]

http://hooktail.maxwell.jp/kagi/7d804de64b64f1c93d6e26b34873cb0e.html

逆に，人間のサイズでは，地球による重力しか感知できないほど，個々の物体同士の重力は小さいですね．そのかわり摩擦などによって容易に電気を発生でき，頭の毛を逆立てることができます．

さらに，小さい領域では，ますます電荷の影響は重力を凌ぐようになります．すると，上に述べた「加速される荷電粒子は電磁波のエネルギーを放出」により不安定になるはずです．ところが，これは量子力学によって，その心配がないことがわかりました．

でも，逆に言えば，十分にゆっくりした粒子運動ならば，クーロン力も重力も同じように考えればよいことが判るとおもいます．以下，それを踏まえて，比例定数kとして

$w\frac{\mathrm{d}^2 \vec r}{\mathrm{d} t^2} = q\frac{k \vec r}{ |\vec r|^{3}}, \tag{1a}$

$k=\frac{Q}{4\pi\varepsilon_{0}}. \tag{1b}$

この運動方程式について，辺々に位置ベクトルの微小変位量 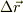$\Delta \vec r$ の内積をとります．これは，力学で習ったと思いますが，力が働いている時に，とれに拮抗しながら微小変位量うごくと仕事量になるからです．でもいまは，天下り式に微小変位の内積をかけたと思ってください．すると面白い式の変形が起こるのです．

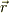計算を進める前に，位置ベクトルの微小変位量と運動の関係を思い出しておきます：運動がおきているとき，ある時刻に，ある位置 $\vec r$ に居るということは，当たり前のことですが

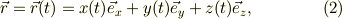
$\vec r= \vec r(t) = x(t)\vec e_{x} + y(t)\vec e_{y} + z(t)\vec e_{z}, \tag{2}$

です．そこで，時間が 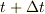$t+\Delta t$ の微量分すすんだ(時間tの微分とも略称する)時の位置の差が，位置ベクトルの微小変位量 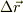$\Delta \vec r$ であると考えるわけです．

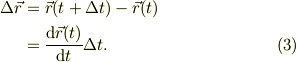
$\Delta \vec r&= \vec r(t+\Delta t) - \vec r(t)\\&= \frac{\mathrm{d} \vec r(t)}{\mathrm{d} t}\Delta t. \tag{3}$

また，ベクトルの内積の定義から，

$(\vec r)^2 &= \vec r \cdot \vec r \\&= |\vec r|^2 \\&= r^2, \tag{4}$

ここで，

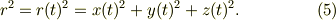
$r^2 = r(t)^2 = x(t)^2 + y(t)^2 + z(t)^2. \tag{5}$

そこで，式(4)の微分を考えると(数学系の人たちが苦虫を噛み潰している音が聞こえてきますが)，一気に

$\vec r \cdot \Delta \vec r = r \Delta r, \tag{6a}$

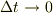と書き直すことが出来ます．もしくは，辺々を $\Delta t$ で割り算し，極限を考えて $\Delta t \to 0$ ；

$\vec r \cdot \frac{\mathrm{d} \vec r}{\mathrm{d} t} = r \frac{\mathrm{d} r}{\mathrm{d} t}, \tag{6b}$

と考えた方が判り易ければ，これでも良いです．

そこで，いよいよ式(1)に対して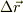， $\Delta \vec r$ の内積をとってみましょう．

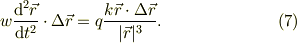
$w\frac{\mathrm{d}^2 \vec r}{\mathrm{d} t^2}\cdot \Delta \vec r = q\frac{k \vec r \cdot \Delta \vec r}{ |\vec r|^{3}}. \tag{7}$

右辺はなにか簡単になりそうですね．問題は左辺です．左右の辺について，別々に考えましょう：

●式(7)の左辺に付いて●

式(3)の関係を使い，変形すると；

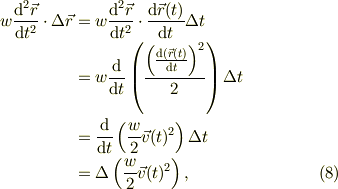
$w\frac{\mathrm{d}^2 \vec r}{\mathrm{d} t^2}\cdot \Delta \vec r&= w\frac{\mathrm{d}^2 \vec r}{\mathrm{d} t^2}\cdot\frac{\mathrm{d} \vec r(t)}{\mathrm{d} t}\Delta t\\&= w\frac{\mathrm{d}}{\mathrm{d} t}\left( \frac{ \left( \frac{\mathrm{d} (\vec r(t)}{\mathrm{d} t} \right) ^2 }{2}\right) \Delta t\\&= \frac{\mathrm{d}}{\mathrm{d} t}\left( \frac{w}{2}\vec v(t)^2 \right) \Delta t\\&= \Delta \left( \frac{w}{2}\vec v(t)^2 \right), \tag{8}$

と，良く知られた運動エネルギーの微分であることが判ります．

●式(7)の右辺に付いて●

ここでは式(6)を利用します：

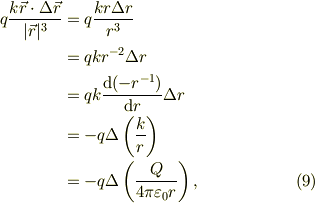
$q\frac{k \vec r \cdot \Delta \vec r}{ |\vec r|^{3}}&= q\frac{k r \Delta r}{ r^{3}}\\&= qkr^{-2}\Delta r \\&= qk\frac{\mathrm{d} (-r^{-1})}{\mathrm{d} r}\Delta r \\&= -q\Delta \left( \frac{k}{r} \right) \\&= -q\Delta \left( \frac{Q}{4\pi\varepsilon_{0}r} \right), \tag{9}$

と，固定電荷が運動電荷の場所に生じている静電ポテンシャルの微分に運動電荷の積がついている事がわかります．

これらの左右辺々の変形式(8),(9)をあわせると；

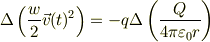
$\Delta \left( \frac{w}{2}\vec v(t)^2 \right)=-q\Delta \left( \frac{Q}{4\pi\varepsilon_{0}r} \right)$

上式で，微分量を纏めると，

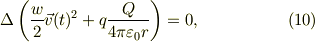
$\Delta \left( \frac{w}{2}\vec v(t)^2 +q \frac{Q}{4\pi\varepsilon_{0}r} \right) =0, \tag{10}$

となり，括弧の中が，時間に寄らず一定な値をもつ，エネルギー保存則が得られます．

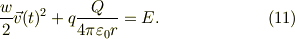
$\frac{w}{2}\vec v(t)^2 +q \frac{Q}{4\pi\varepsilon_{0}r} =E. \tag{11}$

左から，運動エネルギー，静電エネルギー，等号を挟んで全エネルギーです．

式(0)で述べた重力項を含めて考えれば,直ちに拡張できて；

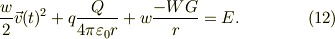
$\frac{w}{2}\vec v(t)^2 +q \frac{Q}{4\pi\varepsilon_{0}r} + w\frac{-WG}{r} =E. \tag{12}$

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝【注記】

・「静電エネルギー」，「静電ポテンシャル」などの用語はあやふやです．・数式から適切な用語を補ってください．・間違いがあれば，09-30に最終補正をする予定です．

以上．

Re: 電位　?

いちさんのレス (2006/09/23(Sat) 08:36)

Chippyさん，はじめまして．

いちと言います．

>ご存知のように，地球と月のように大きな質量同士でないと重力は強く働きません(言 >い換えれば重力は弱い相互作用とも言われます)．

＃これは極めて誤解を与えそうな文章なので，念のため．物理用語として「弱い相互作用」は，「重力」と区別して用います．

確かに，重力は，弱い相互作用なのですが，「弱い相互作用」という言葉は，他の意味で使用されることの方が多いです．ですので，英語で，Weak interactionと書かれてあっても重力ではないですし，重力をWeak interactionというと色々と誤解がありそうです．

「４つの力」「弱い相互作用」「Weak interaction」「Beta interaction」等で検索してみてください．

Re: 電位　?

mNeji さんのレス (2006/09/30(Sat) 00:49)

No.12020の発言の修正について．

いちさんのご指摘を受けて，問題発言となった部分を削除いたしました．念のために該当部分を引用します．

ーーーー引用初めーーーー＃いちさんのご指摘により，下記の＃ (言い換えれば重力は弱い相互作用とも言われます)．＃発言を削除いたします．記：2006-09-30, ｍNeji. ーーーー引用終りーーーー

他方，この部分で説明不足だった部分を補強説明してみます．

力の場として，重力と静電力は有名ですが，発生する力と加速度から見ると，典型的に逆の振る舞いをします．

重力の例として，「太陽=地球」の惑星系を取り，静電力の例として「陽子=電子」の水素原子系を取りますと；

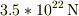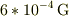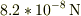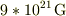<pre> 「太陽=地球」力の大きさ $3.5*10^{22}\unit{N}$ 地球の受ける加速度 $6*10^{-4}\unit{G}$ ，「陽子=電子」力の大きさ $8.2*10^{-8}\unit{N}$ 電子の受ける加速度 $9*10^{21}\unit{G}$ ，

此処で地表での重力加速度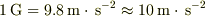， $1\unit{G}=9.8\unit{m}\cdot \unit{s^{-2}} \approx 10\unit{m}\cdot \unit{s^{-2}}$ とした． </pre>

と，力の大きさでは惑星系の方が大きいですが，加速度(力／質量)でみると，圧倒的に水素原子系の方が大きいのです．

従って, 水素原子の法則が，その加速度の大きさの故に古典力学が崩壊して，量子力学に従ったのだとも考えられます．

逆に考えれば，重力で大きな加速度を生み出すような現象にならないと，重力の量子効果は期待できないわけです．従って，宇宙物理学の伸展で，このような状況に接近できれば，面白くなると思われます．

これで，私の解説は終了します．色々な質問をしていただいて有難うございました．

[home] [掲示板] [ページの先頭]

電位 ?

電位　?