和佳 さんの書込 (2006/09/17(Sun) 00:41)

はじめまして．工学部の２年です．テンソルについて質問させてください． 連続体力学でテンソルを使うのでもともと興味のあった解析力学の本などを読んで勉強しようとして躓きました．共変ベクトルのテンソル積axbxcxdを反変ベクトルp,q,r,sを用いて axbxcxd(p,q,r,s)=(a.p)(b.q)(c.r)(d.s)で定義してaxbxcxd(p,q,r,s)を内部積と呼ぶ，というようなことが解析力学の本（山本義隆，深谷賢治など）に書いてありますが，この内部積はテンソル解析の本でテンソルの商法則と読んでいる演算も含むのでしょうか？axbxcxd(p, ,r, )=(a.p)(c.r)bxdというように必ずしも全て反変ベクトルで埋める必要は無いようなので，その点は意味としては商法則と同じなのですが，ここにaxbxcxd(pxq, , )などのように反変ベクトルのテンソル積を入れてもよいのか悩んでいます．このようなことが許されるのであれば，ベクトルを基底にして任意のテンソルを扱えると思うのですが...． 微分形式（反対称共変テンソル場）はdxなどの基底を添えたまま計算するので計算はなじみやすいのですが，連続体力学では反対称テンソル以外も扱うので，基底をつけたまま任意のテンソルの計算をしたいと思っています．物理や多様体の本を見ると微分形式が中心なので，何を読めばいいのかわかりません． それともやはり成分だけ取り出して計算する方法を身につけるしかないのでしょうか？良い本があれば著者とタイトルを教えていただいても助かります． xはテンソル積，.は内積のつもりです．記号がわかりづらいとおもいますが，よろしくお願いします．

mNeji さんのレス (2006/09/17(Sun) 12:04)

はじめまして，和佳さん：

わたしは，通常の流体力学を初めから勉強を始めようとしているものです．

従って，テンソル形式を用いた流体力学を説明できる段階ではありません．しかし，このような高度な質問の場合，どの本を底本にして，どのようなレベルまで勉強したいのかを示されると，回答が付き易いと感じました．

自分も遠い将来，テンソル形式で記述する物理が判ると面白そうだという意味で，和佳さんのご質問に興味があります．

和佳 さんのレス (2006/09/17(Sun) 19:39)

mNejiさん，ありがとうございます．はじめて掲示板を使うため勝手がわからず，不十分な文を書いてしまいました．申し訳ありません．

>通常の流体力学を初めから勉強を始めようとしているものです． 私は主に固体でテンソル解析を必要としています．代数の段階ですでに困っていますが．流体も粘性があるとテンソルが必要になりますよね．お互いがんばりましょう．

>どの本を底本にして，どのようなレベルまで勉強したいのかを示されると，回答が付き易いと感じました． 山本義隆「解析力学I,II」，深谷賢治「解析力学と微分形式」，田代嘉宏「テンソル解析」，松本幸夫「多様体の基礎」は手元にあります．どうせテンソル解析を覚えるなら基底（座標）に依存しない形で身につけたいと思っています．

mNejiさん，アドバイス本当にありがとうございました．

yama さんのレス (2006/09/17(Sun) 21:14)

和佳さん，こんばんは． テンソルについては，詳しいことは分かりませんが・・・ 弾性理論で用いるテンソルは歪みテンソルと応力テンソル，場合によっては粘性テンソルなどだと思います． これらのテンソルはいずれも通常の３次元空間のテンソルなので，一般の多様体上でのテンソル解析の理論は必要としないと思います． また，デカルト座標で考える限り，共変や反変の区別も必要でなく，基底をつけておく必要性もないと思います． 少なくとも当面は，ベクトル解析の延長として理解しておく程度でいいのではないでしょうか．

mNeji さんのレス (2006/09/17(Sun) 22:57)

和佳さん:

>私は主に固体でテンソル解析を必要としています．代数の段階ですでに困っていますが．流体も粘性があるとテンソルが必要になりますよね．お互いがんばりましょう．

なるほど，方向性はわかりました．

>深谷賢治「解析力学と微分形式」

自分も，6月ごろ，こちらの物理かぎプロジェクトのJohさんの数学シリーズの線形代数学系の解説記事：

正式公開記事 - 物理のかぎプロジェクトWiki

• http://hooktail.org/wiki/index.php?%C0%B5%BC%B0%B8%F8%B3%AB%B5%AD%BB%F6

で，テンソルの話を再勉強させていただきました．そのおりに，岩波の「現代数学への入門」のシリーズに触れて，数学の分野から物理を観るという視点もいいものだと思うようになりました．深谷さん，砂田さん，神保さんなどの解説はとても面白いとおもいました．一応，深谷さんの「解析力学と微分形式」を今日，図書館から借りてきました．

Johさんの解説や，「現代数学への入門」のシリーズを大雑把に読み終えた現在，もう一度「解析力学と微分形式」を拝見しました．やはり，実際の物理的な現象をハンドルする為には，物理の系統の本に基づいて，それも通常の3次元ベクトルと，3行3列のマトリックスとしてのテンソル記述の運動方程式の観点でステップ・バイ・ステップで解析に供するのが最短距離では無いかと感じました．

＃恐らく，通常の運動方程式の解析を，自由自在に出来るようになった後に， ＃しばしば使う手馴れた式をテンソル形式にとか外微分形式で書き直して， ＃見通しの良い最適な問題記述を得ることが出来るようになるのでは無いかと， ＃推察しています．

その意味では，yamaさんのご意見に近い感触を持ちます．

なお，流体力学の図書を探している途中で，「連続体の力学，巽 友正・著，岩波書店，2005-04, ISBN:4-00-007922-0」はバランスの善い解説と感じました．素人意見ですので，本屋さんで眺めてみてください．

意外と，流体力学や弾性体運動論は，少数ながら興味をお持ちの方が居るのを知り，心強いです．少数派の牙城として「数式掲示板で意見交換する」のも面白いと思います．行き詰ったら相談しあいましょう．

和佳 さんのレス (2006/09/17(Sun) 23:05)

yamaさん，ありがとうございます． まったくそのとおりです．実際「連続体力学」「固体力学」「弾性論」のようなタイトルで多様体や微分形式を持ち出しているものは見たことがありません．ものによってはデカルト座標でしか成立しない話を一般論との区切りなしに述べている程なので，工学的には「直行曲線座標まで」とか「デカルト座標だけ」というのが一般的だと思います． ただ，狙っている研究室が解析力学や力学系の手法を使うところなのでどうせなら今のうちに一般的な方法を身につけたいと思って質問させていただきました．

和佳 さんのレス (2006/09/17(Sun) 23:26)

mNejiさん，ありがとうございます． >3行3列のマトリックスとしてのテンソル記述の運動方程式の観点でステップ・バイ・ステップで解析に供するのが最短距離では無いかと感じました． 確かに後期の授業では行列か成分計算で十分です．

>意外と，流体力学や弾性体運動論は，少数ながら興味をお持ちの方が居るのを知り，心強いです．少数派の牙城として「数式掲示板で意見交換する」のも面白いと思います．行き詰ったら相談しあいましょう． そうですね，ありがとうございます．確かに地味な感じもあり，興味を持ちづらいのかもしれませんね．

MXK さんのレス (2006/09/17(Sun) 23:46)

axbxcxd(pxq, , ) はむしろ，pxqxcxd(a,b, , ) などと書くべきなのかも 知れませんが，意味は十分分かりますね． 添字記法では 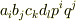と悩まずに 書けます．テンソル積がテンソルになっても 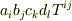と書けます． テンソルの関数表記は定義としてはいいのですが，実用的には 結構窮屈なので，添字記法もマスターされた方がいいと思います．

和佳 さんのレス (2006/09/18(Mon) 00:43)

MXKさん，ありがとうございます． >axbxcxd(pxq, , ) はむしろ，pxqxcxd(a,b, , ) などと書くべきなのかも知れませんが，意味は十分分かりますね．添字記法ではa_i b_j c_k d_l p^i q^jと悩まずに書けます． （すみません．数式の使い方がわからなくておかしなことになってますがお許しください）

確かに添え字を使うと（axbxcxd(pxq, , ) が許されるのであれば）pxqxcxd(a,b, , ) と同じだとわかりますね．ただ，axbxcxdでひとつの物理量，pxqでひとつの物理量をなしている場合，たとえばS=S_ijkl(e^i)x(e^j)x(e^k)x(e^l)とT=T^(ij)(e_i)x(e_j)についてa=e^iなどとすればは少なくとも最初はaxbxcxd(pxq, , )が自然な気がしますが，いかがでしょうか？

>テンソル積がテンソルになってもa_i b_j c_k d_l T^{ij}と書けます．

そうですね．T=T^(ij)(e_i)x(e_j)とすればp=e_iq=e_jとして基底eに関して 同じことができるので，問題ないと思っていました．

>テンソルの関数表記は定義としてはいいのですが，実用的には結構窮屈なので，添字記法もマスターされた方がいいと思います．

実力も無いのに道を狭めている気がしてきました．添え字でも勉強してみます．好き勝手するにしても，添え字記法ができるようになってからにします．

MXK さんのレス (2006/09/18(Mon) 11:39)

> axbxcxd(pxq, , )が自然な気がしますが，いかがでしょうか？

自然な拡張なので問題ないと思います． axbxcxd(pxq, , )=axbxcxd(pxq( ,e), pxq(f, ), , )/(q.e)(p.f) とでも定義しておけばいいのでしょう．

しかし，拡張をすすめても，いずれ S_{ijk}T^{ji}, S_{ijk}T^{ik} などで行き詰まると思います．

添字記法は成分を用いていて表面的には座標依存に見えますが， 見方を変えると必ずしもそうではありません．

座標フリーは重要な立場ですから，ぜひ貫徹してください． 安易に成分に頼らないという姿勢はとてもよいと思います．

yama さんのレス (2006/09/18(Mon) 12:13)

pxqxcxd(a,b, , )=axbxcxd(p,q, , ) だと思いますが，これを axbxcxd(pxq, , ) と書いてもいいのでしょうか？ この書き方ができるのなら，axbxcxd(p,q,r,s) を axbxcxd(pxqxrxs) と書いてもいいように思うのですが・・・．

もちろん， axbxcxd(pxqxrxs)=axbxcxd(p,q,r,s)=(a.p)(b.q)(c.r)(d.s) と定義しておけばいいのだとは思いますが，一般的に用いられる記法ではないように思います．

和佳 さんのレス (2006/09/18(Mon) 16:42)

MXKさん，ありがとうございます． > axbxcxd(pxq, , )=axbxcxd(pxq( ,e), pxq(f, ), , )/(q.e)(p.f)とでも定義しておけばいいのでしょう． なるほど，導出できない以上定義を増やすしかないですね...．確かに限界がありそうです．定義を増やすのも良くないでしょうし．

> S_{ijk}T^{ji}, S_{ijk}T^{ik} などで行き詰まると思います．

頂いた定義を使えば基底に関して同じことができるので問題は無いですが，基底で計算すると代数らしくなる，アインシュタインの規約を意識しなくていい，という程度で，１次結合を全部書くことを考えるとあまりいいこと無いですね．

> 添字記法は成分を用いていて表面的には座標依存に見えますが，

見方を変えると必ずしもそうではありません．

確かに，添え字を上下に振って反変，共変を区別している以上自然基底を使っていることになり，座標を決めていませんね．

yamaさん，ありがとうございます． > この書き方ができるのなら，axbxcxd(p,q,r,s) を axbxcxd(pxqxrxs) と書いてもいいように思うのですが・・・．

最初の質問の意図はそういうことです．イコールを使わなかったので伝わらなかったのかもしれません．申し訳ありません． axbxcxd(p,q,r,s)=axbxcxd(pxqxrxs)で良いのかということです． 数学的には区別する意味がなさそうですが，物理的にはs=C(e)つまりs_ij=C_ijkl e^kl（応力=弾性係数x歪）など，テンソルにテンソルを作用させる（ここでは２階のテンソルに４階のテンソル）状況もあるので書く上では区別が必要だと思います．

和佳 さんのレス (2006/09/18(Mon) 16:59)

関数記法ではs=C(e)よりs=C( , ,e)ですね．申し訳ない．

MXK さんのレス (2006/09/18(Mon) 17:40)

関数記法で無理すると，

s( , ) = sum_k sum_l C( , ,e^k,e^l)e(e_k,e_l)

となるわけだから，実質的に添字記法と同じことになって しまいます．

yama さんのレス (2006/09/18(Mon) 18:16)

axbxcxd(p,q,r,s)=axbxcxd(pxqxrxs) と定義しても矛盾はおきないと思いますが，あまり必要性がないように思います．

弾性率テンソルも歪テンソルもベクトルのテンソル積で表されるわけではないので，これらの積を表す場合，axbxcxd(p,q, , )とaxbxcxd(pxq, , ) のどちらも無理があるように思います． 基底をつければ，どちらの表し方もできそうですが，煩雑になりそうです．

Joh さんのレス (2006/09/18(Mon) 18:49)

週末ネットにつなげなかったので，面白そうな議論に乗り遅れました．．． 問題は解決してますね．．．

yama さんのレス (2006/09/18(Mon) 20:33)

よく考えてみると，基底をつけるかどうかに関係なく s_ij=C_ijkl e^kl（応力=弾性係数x歪）を axbxcxd(p,q, , ) の形に表すことは無理のように思われます． というのは，C_ijkl の成分81個のうち，対称性を考えると相異なるものが21個あります． しかし，４個のベクトル a,b,c,dの成分は合わせて12個しかありません． 従ってテンソルCを，４個のベクトルのテンソル積 axbxcxd で表すことは一般にはできないと思います．

和佳 さんのレス (2006/09/18(Mon) 21:45)

MXKさん，Johさん，yamaさん，ありがとうございます．

> s_ij=C_ijkl e^kl（応力=弾性係数x歪）を

axbxcxd(p,q, , ) の形に表すことは無理のように思われます． > 従ってテンソルCを，４個のベクトルのテンソル積 axbxcxd で表すことは一般にはできないと思います．

そのとおりです．任意のテンソルを１つのテンソル積で表現することはできません．しかしテンソル積の１次結合で表すことはできるので，axbxcxdについてできれば，その議論を基底に関して適用してやればいいわけです．ただ，MXKさんのおっしゃるように微分形式と違って成分で計算するのとあまり違いが無いんですよね...．

mNeji さんのレス (2006/09/18(Mon) 22:00)

横から失礼します.

素人質問がふたつあります．

1. テンソルの表現について

「共変ベクトルのテンソル積axbxcxd」といった表現を始めて拝見するのですが，どんな本にでていて，どのようなメリットが在るのでしょうか？

2. 固体物理・流体力学でのテンソル表現の有用性

流体力学の初心者ですが，運動方程式をテンソル形式で記述することを目指されていらっしゃるようですね．これは自由度が大きい場合に有効だとか，特殊な座標系を導入する為だとか，特別な物理的背景があるのでしょうか？

例えば，天文学的規模の電磁流体での波動現象で，運動速度がとても大きくて相対論的取り扱いが本質的なような場合ですと，テンソル形式の処理が必要な気もしますが...．

yama さんのレス (2006/09/18(Mon) 22:15)

テンソルをテンソル積の１次結合で表すとすると，テンソルどうしの積は１つの内部積では表せず，多数の内部積の和になると思います． さらにこの場合は，１次結合で表すための計算も必要になります． そうなると，計算も表式も複雑になってしまって，内部積を用いるメリットはほとんどなくなると思うのですが・・・．

和佳 さんのレス (2006/09/18(Mon) 22:40)

ほかの方に答えていただけるでしょうが，私の意見という程度で読んでいただけたらと...． (2)から． > 流体力学の初心者ですが，運動方程式をテンソル形式で記述することを目指されていらっしゃるようですね． この「テンソル形式」がある意味最も一般的である添え字の演算としてのテンソル解析を指すならば，そうではありませんでした．むしろそれを避けようとして質問しました．a,bなどは太字と思ってください．今は添え字も覚えようと思っていますが．

> これは自由度が大きい場合に有効だとか，特殊な座標系を導入する為だとか，特別な物理的背景があるのでしょうか？

特殊な状況ではありません．扱う物理量が応力や歪などテンソルである以上テンソル解析はむしろ当然です．河合俊治「特殊相対性理論の数学的基礎」によると，物理量は全てテンソルであり，物理法則はその関係式だそうです（スカラーは０階，ベクトルは１階のテンソル）．つまり物理をやっている以上常にテンソルを扱っているわけです．

(1) mNejiさんは「解析力学と微分形式」は読んでいますよね？それにも微分形式という名前で反対称共変テンソル場と（反変）ベクトル場は登場していませんか？ > どの本を底本にして，どのようなレベルまで勉強したいのかを示されると，回答が付き易いと感じました． というmNejiさんのアドバイスに従って挙げた山本義隆「解析力学I,II」，田代嘉宏「テンソル解析」，松本幸夫「多様体の基礎」や「特殊相対性理論の数学的基礎」 などにも載っています（名前はいろいろですが）． メリットというよりは，反変，凶変を区別しないと自然基底は扱えません．

和佳 さんのレス (2006/09/18(Mon) 22:49)

yamaさん，ありがとうございます． > テンソルをテンソル積の１次結合で表すとすると，テンソルどうしの積は１つの内部積では表せず，多数の内部積の和になると思います． そのとおりです．面倒になるばかりなんですよね...．

> １次結合で表すための計算も必要になります．

これは必要ありません．C=C_ijkl e^i x e^j x e ^k x e ^lで，MXKさんの言葉ですが > 実質的に添字記法と同じことになってしまいます． つまり純粋に基底があるかないかだけの違いになります．

yama さんのレス (2006/09/18(Mon) 22:54)

なるほど，確かにその通りですね．

和佳 さんのレス (2006/09/18(Mon) 23:17)

やはり微分形式の表現は反対称だからこそ生きるということでしょうか...．

yama さんのレス (2006/09/18(Mon) 23:54)

反対称でなければ微分形式で表されないのだから，当然そういうことになるでしょうね．

mNeji さんのレス (2006/09/18(Mon) 23:55)

和佳さん：

>山本義隆「解析力学I,II」，田代嘉宏「テンソル解析」，松本幸夫「多様体の基礎」や「特殊相対性理論の数学的基礎」 などにも載っています（名前はいろいろですが）． メリットというよりは，反変，凶変を区別しないと自然基底は扱えません．

一度，これらの本を拝見したいとおもいます．まだ数学的な意味での反変・共変の関係を熟知していないのですが，通常の直交座標系ではそれらの区別はないですよね．

>扱う物理量が応力や歪などテンソルである以上テンソル解析はむしろ当然です．河合俊治「特殊相対性理論の数学的基礎」によると，物理量は全てテンソルであり，物理法則はその関係式だそうです（スカラーは０階，ベクトルは１階のテンソル）．つまり物理をやっている以上常にテンソルを扱っているわけです．

だからといって，力学とか電磁気をテンソル形式で扱うかどうかは別問題ではありませんか？特にスカラとベクタだけの世界にテンソルを持ち込んでも手間が掛かるだけですね．

もちろん，2階のテンソルとしてテンソルが必要な場合，連立方程式が複雑になり，テンソル算法が本質的になるかもしれません（自分ではそのような解析をしたことが無いので)．でも，それなりに主要項を対角成分となるようにして，通常の解析をしたり，残りを摂動項として部分的に処理するとか「物理的な処理方法」があろうかと推測しました．

勿論，理論的研究対象としてのテンソルが無駄だと申し上げているわけではありません．ご紹介の図書を勉強のうえ，今回のご論議を参考にさせていただきます．

MXK さんのレス (2006/09/18(Mon) 23:59)

反対称の場合，自由度が少ない，内部積の自由度も少ない，主に共変部分だけ を考えればいい，などが効いているのではないでしょうか．

和佳 さんのレス (2006/09/19(Tue) 00:47)

> だからといって，力学とか電磁気をテンソル形式で扱うかどうかは別問題ではありませんか？特にスカラとベクタだけの世界にテンソルを持ち込んでも手間が掛かるだけですね． 「テンソル形式」が何を指すのかわかりませんが，太字で計算する場合はベクトルまでしか登場しないのであれば２階以上ののテンソルは持ち込みようがありません． 成分計算を指すのであれば，対称性からある成分だけ拾って計算するというのは力学や電磁気でもよくやりますよね．あえて言えば添え字をi,j,kとすることですが，これはi=x,y,zなどをまとめているだけなので，「テンソル形式」がどこで線引きされているのか教えていただけないでしょうか．

> 反対称の場合，自由度が少ない，内部積の自由度も少ない，主に共変部分だけ

を考えればいい，などが効いているのではないでしょうか． なるほど．だから微分形式は画期的なのでしょうね．

mNeji さんのレス (2006/09/19(Tue) 01:00)

和佳さん：

先ほどは，ややネガティブな感じで書いてしまいましたが，テンソル形式に付いてはかなり興味があります．でも，流体力学もまた未着手のなので推測でしかないので，言うのを憚りました．

しかし，一つの予測として書いて見ます．馬鹿げているかもしれませんので，嫌でしたら無視してください．

私が流体力学を知りたいのは，先ず「掌や足が水を押していく時の推進力を効果的にし，その後部に出来る水の渦の減速力を効果的に減少させるか」が知りたいのです．おそらくこれは，通常の流体力学で処理できると考えています．

その次に知りたいのは，「効率的な運動は何か？」を知りたいのです．特にクロールでは，体の軸に関する回転(ローリング)が起こります．これも含めて，人体の運動を記述しようとすると，体の回転も含めた，多関節モデル計算が必要となります．多関節自体は，ロボットの運動の解析で，最近はお猿さんが木の枝を片手でつまみながらの運動まで記述できるほど進化しているようです．

でも水泳の場合，そのような束縛点が存在しないうえ，体が水の上下を行き来すらします．手や足の運動に従い，水につかる部分までが時間依存で替わるわけです．

このような課題をどうすればいいのか判りません．でも，重力場での運動で，極座標系で記述することで回転運動が見通しが利くように，ローリング座標を使えば，記述が楽になると思えます．

そうすると，水泳の解析では，関節ごとに質量と慣性モーメントをもち，それらの角度がパラメータの動的座標と慣性モーメント・テンソルをハンドルする必要があろうと考えています．

現在の自分の能力では，とうてい具体化できない問題ですが，一歩でもそんな解析に近付きたいと思っています．

一寸，想像だけの話で，失礼しました．

和佳 さんのレス (2006/09/19(Tue) 02:07)

応用上の目標があるのは勉強がはかどりそうですね．工学部にいるのでまわりにはそういう人が多いですが，私自身は応用的な知識はまだまったく持っていません．機械系なのに車などの乗り物が嫌いなほどです．解析力学〜力学系を使う研究室を狙ってはいますが，その研究室の目的はロボットか何かの制御で，解析力学〜力学系は道具に過ぎないので，ほかの研究室にしようかと思ってしまうこともあります．mNejiさんのような応用的な視点を身につけたいと思ってはいるのですが，きっかけがないとなかなか...．流体力学に対する興味の持ち方としてとてもすばらしいと思います．がんばってください．

mNeji さんのレス (2006/09/19(Tue) 15:32)

和佳さん：

>応用上の目標があるのは勉強がはかどりそうですね．工学部にいるのでまわりにはそういう人が多いですが，私自身は応用的な知識はまだまったく持っていません．

2年生では，まだ強い目標を持たなくても良いと思います．むしろあまりにも狭い範囲に勉強を絞り込むのも考え物です．

自分のばあいは，とある電磁気の本にのめりこみ，量子力学や解析力学もすべて電磁気の本から解釈をして理解していました．ある意味，考え方が明確になり，あちこちの知識がなくても，一から考えれば済むので，思考の効率化を図れると思っていました．でも，その代り，新しい計算法などを利用するのに時間がかかるなどの弊害があります．

ある意味で，時代の流れとも仲良く進んだ方が楽だし，効率も良いという例です．でも，逆に2年生で，いろんな分野の勉強をされているのですから，卒研のテーマは，すこしリラックスして悠然と構えるのも良いですよ．

自分は，水泳の解析を興味があるようになったとき，大昔，解析力学で見た一般座標系の話が，ロボット工学でこんなに展開されているのにとても驚きました．わが国のロボット工学は「鉄腕アトムの漫画があるから世界に先駆けているのさ」という浅はかな理解をしていた自分が恥ずかしかったです．

で，ロボット工学が終わったかというと，人間に近い運動として，体の捩れや，腕や脚の捩れはまだまだ未知の領域があると思います．目的行動を決めたとして，演繹的に体の運動をだせるにはほど遠いと思います．

まだまだ解析力学的な深い理解が必要であろうと思います．そのような未知領域の研究には，種々の数学的概念の利用が必要でしょうから，広義のベクトル解析としてのテンソルやその周辺，空間把握の数学的な手法など，従来関係なかったような分野を勉強する必要があろうかと推察しています．

ですから，「自動車が嫌いなのに自動車の研究室」というのは止めた方がいいと思いますが，ロボットの研究室などは，数学的基礎を固めながら，実際の応用に手を染めるチャンスとして捕らえるのもあるように感じました．

>機械系なのに車などの乗り物が嫌いなほどです．解析力学〜力学系を使う研究室を狙ってはいますが，その研究室の目的はロボットか何かの制御で，解析力学〜力学系は道具に過ぎないので，ほかの研究室にしようかと思ってしまうこともあります．

ですから，「自動車が嫌いなのに自動車の研究室」というのは止めた方がいいと思いますが，ロボットの研究室などは，数学的基礎を固めながら，実際の応用に手を染めるチャンスとして捕らえるのもあるように感じました．

どうせ，卒研は，泣いても笑っても，1年間だけですよね．

>mNejiさんのような応用的な視点を身につけたいと思ってはいるのですが，きっかけがないとなかなか...．流体力学に対する興味の持ち方としてとてもすばらしいと思います．がんばってください．

はい，負けずに楽しみます．

なお，今回，コメントを下さっている方々は，物理数学については詳しくご存知な方々とおもいます．納得のいくまで，じっくりと論議をされると素晴らしいと思います．

toorisugari no Hiro さんのレス (2006/09/19(Tue) 15:52)

Johさんと同じく，乗り遅れて議論に参加できなかったんですが，まだ，続いてる!

寄与できるような発言はもうできませんが，いくつか口を挟ませてください．

私も和佳さんと同じ様な事を考えていました．私はCartesian座標系が嫌いで，ベクトルやテンソルを添え字で考えるのが嫌いです．

ベクトルの場合は添え字記法を使わなくても，図形的に考えることが可能です．すなわち，座標系や計量によらない「ベクトル」という存在があることを意識して理論ができる．

同じようにテンソルでもできないかを考えているのですが，すでにMXKさんが触れられているように，厳しいようです．理由はひとえに，テンソルを線形関数としてみたとき，その関数は引き数が多く順番が意味を持つ事につきます．

これを意識した簡単な表示法は「見かけ上座標系に依存する」添え字表示しかないのです．(まだ，あきらめてはいませんが．．．)

完全反対称テンソルに話を限るのなら，ご存じの通り話は簡単ですが，対称テンソルまで考えると，さらに一般のテンソルまでカバーするとなると厳しいですね．

ともかく，工学部の2回生でこのようなことに関心を持たれていることに驚きを感じます．自然基底や反変共変テンソルをここまで理解されて，さらに座標系に依存しない議論に関心を持たれているなんて!

物理の学生でも相対論に興味を持ちだして(理解できるようになって)から(4回生以降?) ，和佳さんのような疑問を持つのに!!

もし興味をお持ちならこのまま一般相対論まで勉強されるのも手かもしれません． (テンソルを理解するにはこれが一番でしょう．)

Joh さんのレス (2006/09/19(Tue) 16:49)

最初の議論には乗り遅れたんですが，その後の議論もレベルが高く，ちょこちょこ調べたり復習しているうちに更に置いてけ堀を食らっていた，というのが正直なところです．でも，なんだか議論は終結し，みなさんがテンソル感を述べ合っているようなので，僭越ながら混ぜていただきます^^

toorisugari no Hiroさんもおっしゃっているように，工学部２年にしては，本当に深い洞察力をお持ちだと思います．座標系に依存しない表現というなら，やはり微分形式を追求されるといいでしょう．（でも，工学部２年で多様体なんて出てこないですよね！御自分で勉強なさっているんですね．素晴らしいことです．）

和佳さんがどこかに，全ての物理量はテンソルで記述できると書いていましたが，量子力学のスピンなどは，テンソルでは書けませんので，「ほぼ全ての物理量は」と直すべき，と思います．相対論はもちろんテンソルが大活躍の分野ですから，大いにやられたらいいと思います．座標系について興味がおありなら，多様体の理論をもっとつきつめても良いかもしれません．

ｙama さんのレス (2006/09/19(Tue) 16:59)

解析力学〜力学系に興味があるなら，その方面の大学院へ進むという選択肢もあると思います． たとえば，工学部３年生の時に「工学部で学ぶ数学」を著されたという千葉逸人氏は，情報学研究科に進まれて数理物理学，力学系理論を専門とされているようです． 氏のホームページ

• http://www.geocities.jp/ruy406/index.html

には数学関係のいろいろな記事があり，微分形式や多様体についての解説もあるので参考になると思います．

toorisugari no Hiro さんのレス (2006/09/19(Tue) 18:19)

mNejiさん:

わかる範囲で．

> (1) テンソルの表現について
> 「共変ベクトルのテンソル積axbxcxd」といった表現を始めて拝見するのですが，どんな本にでていて，どのようなメリットが在るのでしょうか？

本はたとえば前に紹介した本があります．

• http://www.amazon.co.jp/gp/product/4320018176/

メリット...これができないとそもそも成分表示(添え字表示)ができません．テンソルは複数の添え字をもち座標回転で反変あるいは共変する量という定義から出発するなら話はべつですが(でも，それだと物理的幾何学的実体が見えない)．

上の表示はテンソルの中の特別なもの(純テンソル)の定義ですね．これ(ら)を基底にして成分表示ができます．

> (2) 固体物理・流体力学でのテンソル表現の有用性

数値計算には，精度を考えて保存則を意識した計算法があります．そこではベクトル方程式であるNS方程式を差分化するのでなく，テンソルを含む運動量保存則

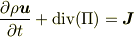
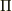( は運動量輸送等を記述するテンソル) を差分化します．元の方程式は等値でも差分化した式は違います．性能は後者が上だそうです．

mNeji さんのレス (2006/09/19(Tue) 20:12)

toorisugari no Hiroさん：

>本はたとえば前に紹介した本があります． > http://www.amazon.co.jp/gp/product/4320018176/

夏に神田の古本屋さんにいったおり，日本語のテンソルの本は入手できたんですが，この本はなく，三省堂でもなく，丸善にいこうかと思ったのですが，暑さにめげて，行きませんでした． 年貢の納め時かもしれませんね(笑)．

>メリット...これができないとそもそも成分表示(添え字表示)ができません．テンソルは複数の添え字をもち座標回転で反変あるいは共変する量という定義から出発するなら話はべつですが(でも，それだと物理的幾何学的実体が見えない)．

誘電率テンソルとかはベクトルとベクトルをむすぶマトリックスとイメージで納得しただけですし，マクスウェル方程式をローレンツ変換する時の形式的な座標変換手段みたいな所で，記憶が凍っています，というかそれ以上深く勉強していません．今後，中期的に勉強したいと思いはじめています．

>上の表示はテンソルの中の特別なもの(純テンソル)の定義ですね．これ(ら)を基底にして成分表示ができます．

ようやく和佳さんのご質問レベルに近付いたようですね．折角の機会ですから手をだしてみようかな．

>数値計算には，精度を考えて保存則を意識した計算法があります．そこではベクトル方程式であるNS方程式を差分化するのでなく，テンソルを含む運動量保存則を差分化します．元の方程式は等値でも差分化した式は違います．性能は後者が上だそうです．

歳を取るに釣れ，功利的な意識が高まるようで，なるほど納得です．

和佳 さんのレス (2006/09/20(Wed) 00:29)

> 私も和佳さんと同じ様な事を考えていました．私はCartesian座標系が嫌いで，ベクトルやテンソルを添え字で考えるのが嫌いです． > これを意識した簡単な表示法は「見かけ上座標系に依存する」添え字表示しかないのです．(まだ，あきらめてはいませんが．．．) > 完全反対称テンソルに話を限るのなら，ご存じの通り話は簡単ですが，対称テンソルまで考えると，さらに一般のテンソルまでカバーするとなると厳しいですね．

やはりそうなんですね．やはり他の人も同じことを考えると知って安心しました．わたしも正直完全にはあきらめていません（笑）

> 和佳さんがどこかに，全ての物理量はテンソルで記述できると書いていましたが，量子力学のスピンなどは，テンソルでは書けませんので，「ほぼ全ての物理量は」と直すべき，と思います．

「特殊相対性理論の数学的基礎」にもそのように書いてありました． 『「物理量はすべて時空におけるテンソル量であって，物理法則はこれらの量に関する方程式である」という内容は通例一般相対性原理と呼ばれている．我々は，「時間と空間を合わせたものはMinkowski時空であることと一般相対性原理」を基本的前提とするのである．なお，素粒子論においては，電子やクオークも扱う．このような場面では，スピノル量も現れる．』

自分の理解の範囲で勝手に文章を落としてはいけない場合も多いということですね．申し訳ありません．一般相対性原理は，古典論での公理の１つと思えばいいのでしょうか...．

> 解析力学〜力学系に興味があるなら，その方面の大学院へ進むという選択肢もあると思います．

たとえば，工学部３年生の時に「工学部で学ぶ数学」を著されたという千葉逸人氏は，情報学研究科に進まれて数理物理学，力学系理論を専門とされているようです．

「工学部→工学部の修士」であるにも関わらず，数理物理学，力学系理論をやっているということでしょうか？そのようなことが可能とは思いませんでしたが，「工学部→理学部の修士」よりは現実的なのでしょうか？ 転学部を考えていましたが，２年前期の成績は悲劇的だと思うので（材料関係の授業がとくにひどかったです．フェライト，パーライト，共析反応など，さっぱりでした...）無理ですね． 相対論，量子論などを知らないと理学部修士の受験は無理ですよね？

mNeji さんのレス (2006/09/20(Wed) 01:07)

>情報学研究科

最近は，兎に角新しい名前の付いた組織にならないと生き残れないといった感じがつよく，その文字をそのままで了解するととんでもない場合もあります．せめてインターネットで研究業績リストや経歴などを見てから判断した方がいいと思います．

>「工学部→理学部の修士」 >２年前期の成績は悲劇的だと思うので（材料関係の授業

そのようなケースを知らないのですが，基礎学科の成績が確りしていれば，工学系の授業の点数などそれほど気にしないと思いますけど． 何といっても，試験と，面接が大事だと思います．

>相対論，量子論などを知らないと理学部修士の受験は無理ですよね？

量子力学は物理的な意味，波動関数の処理，などを見るために必須と思います．

相対論はそれこそ相手の専門に近ければ出るでしょうし，物性物理を狙えば，余程のことが無い限りでないと言えると思います．

＝＝＝＝ 近くの図書館で，ベクトル解析の復習用に

岩波講座 応用数学 [基礎 6] ベクトル解析と多様体I,II 小松 彦三郎・著 1995年

を借りてみました．IIでは，「テンソル代数とグラスマン代数」から始り，物理的な雰囲気の強い説明が在るようです．中期的に勉強しようとおもいました．解説する側が勉強を始めるなんて，影響力の強い質問をされたと感心しています．では，失礼します．

toorisugari no Hiro さんのレス (2006/09/20(Wed) 01:09)

> わたしも正直完全にはあきらめていません（笑）

がんばりましょう．(^^)

> 「工学部→理学部の修士」よりは現実的なのでしょうか？

転学部をしないでも研究は可能というだけで，転学部を考えているのでしたら，修士からでもB3からでも「現実的」だと思います．

> 転学部を考えていましたが，２年前期の成績は悲劇的だと思うので
> (略)
> 無理ですね．

2年前期の成績より入試時の成績が重要です．でも，なにより「熱い思い」を語ることが大事だと思います．

> 相対論，量子論などを知らないと理学部修士の受験は無理ですよね？

力学と電磁気学と基礎的な数学をしっかり押さえれば何とかなるのでは? (量子論と統計力学も勉強はしなければいけないですが．)

Joh さんのレス (2006/09/20(Wed) 03:24)

修士の受験も転学部も可能だと思いますよ．

もちろん，御自分の大学のことはよく御存知だと思いますが， 大学の先生が看板通りの研究をしているわけではありませんし， 転学や入学の基準も学校や個々の先生によって違うでしょう． 十分に行く先のことを調べるのはまず大事ですが，多分，和佳さん が思っているよりも，熱意でなんとかなる場合が多いんじゃ ないでしょうか．

私は自分の大学のことしか分かりませんので，一般論は 何も言えませんが，まず色々な意見を聞くといいと思います． 善は急げです．

ｙama さんのレス (2006/09/20(Wed) 08:56)

京大の情報学研究科は工学部情報学科との関係が深いようですが，工学研究科とは別になっています． 数理工学専攻の中に力学系理論の講座があるようです．

• http://www.amp.i.kyoto-u.ac.jp/intro.html

mNeji さんのレス (2006/09/20(Wed) 10:31)

自分が述べた意見：

>>「工学部→理学部の修士」 >>２年前期の成績は悲劇的だと思うので（材料関係の授業 > >そのようなケースを知らないのですが，基礎学科の成績が確りしていれば，

について，修正意見です．

ずいぶん前(30年以上)のことですが東大の実験系の物理の方です．出身は工学部の「物理工学科(？あやふや)」で，物理の大学院に入られたとおもいます．夏の学校でお聞きしたのを思い出しました．少なくとも，「工学部→理学部」の一例ではあります．

そういえば，自分のいた研究室では，学内の場合ですが，「理学部→工学部」が一時急増したことがあります．最近は，大学院の定員が増加したり，外部への枠を増やしたりで，状況は変わっていると思いますが．

いずれにせよ，インターネットなどに各種の情報を調べるのも良いのでは？

mNeji さんのレス (2006/09/20(Wed) 11:54)

追伸：

さらに思い出しました，学内間の移動の方ですが，「工学部・化学工学科」→「大学院理工学研究科・物理学専攻」に移られたとおもいます．物性物理に興味があったのと電磁気も好きだといってられました．とてもよく質問される方でした．

自分の記憶だけでも数件あるのですから，制度的には十分に可能と思われます．先ずは，現状把握が大切ですね．

toorisugari no Hiro さんのレス (2006/09/20(Wed) 12:22)

>> 「物理量はすべて時空におけるテンソル量であって，物理法則はこれらの量に関する方程式である」という内容は通例一般相対性原理と呼ばれている．

私の知っている一般相対性原理は「物理法則は任意の運動をしているどんな座標系からみてもその数学的表現形式が同じである．」ですが，はっ，これって添え字表示を念頭にした，つまり座標系を意識した定義ではないですか．それに比べて上の定義は「テンソルは座標系に関係なく存在する」を念頭にした定義ですね．

ああ，まだ，頭がcoordinate-dependentだった．．．．orz

勉強になりました．

> 一般相対性原理は，古典論での公理の１つと思えばいいのでしょうか...．

公理とよぶか要請と呼ぶかは微妙ですが，そう思われて良いです．たぶんどのように物理が進展しても，これが拡大することはあれ，覆されることはないでしょう．(局所的に平坦な時空という概念が完全に破棄されない限り)

和佳 さんのレス (2006/09/20(Wed) 16:16)

なるほど．どれも参考になります． 修士から理学部というのはぜんぜん非常識じゃないんですね．いわれてみれば，試験で受かれば問題ないわけですしね．

> 京大の情報学研究科は工学部情報学科との関係が深いようですが，工学研究科とは別になっています．

数理工学専攻の中に力学系理論の講座があるようです．

大学院は理学部，工学部に限らないんですね...．

> 公理とよぶか要請と呼ぶかは微妙ですが，そう思われて良いです．

このへんはときどき悩みます．「公理」だと「いつでも成り立つ」という印象が強すぎる気がします．ニュートンの運動方程式もこの類だと思いますが，これもいつでも成り立つわけではないですよね...．「要請」だとこちらが決め付けている印象が強い気がしますし，「仮定」だと意味そのものが弱いですよね...．

和佳 さんのレス (2006/09/20(Wed) 16:38)

こちらで解説やアドバイスを受けて，しばらく「添え字の演算」としてのテンソルに集中しようと思うようになりました．何か本を紹介していただけないでしょうか？ 田代嘉宏「テンソル解析」は２階のテンソルが中心なので行列を平気で使っていますが，３階以上のことを考えると極力行列を排除したものが良い気がするのですが...．

> もし興味をお持ちならこのまま一般相対論まで勉強されるのも手かもしれません．

(テンソルを理解するにはこれが一番でしょう．)

ということで，相対論の本でも全然かまいません． よろしくお願いします．

toorisugari no Hiro さんのレス (2006/09/20(Wed) 17:59)

> こちらで解説やアドバイスを受けて，しばらく「添え字の演算」としてのテンソルに集中しようと思うようになりました．何か本を紹介していただけないでしょうか？

すでに何回か紹介している本ですが，

テンソル―科学技術のために 石原 繁

• http://www.amazon.co.jp/gp/product/4785310685/

物理屋向けの古典的なテンソル解析の入門書です．Cartesian座標系で始まっているので，双対の概念は斜交座標系が出てからです．モダンな概念で習った人には物足りないかも．でも，著者はモダンをわかっていて，あえて古典で書いてる節がありますし，スタンダードな概念を押さえるのにはよいと思います．

現代ベクトル解析の原理と応用 新井 朝雄

• http://www.amazon.co.jp/gp/product/4320018176/

ベクトルは絶対的存在だー．と叫ぶ著者の本．数学者らしくモダンですが，物理屋がわかるように書いています．

Geometrical Vectors (Chicago Lectures in Physics) Gabriel Weinreich

• http://www.amazon.co.jp/gp/product/0226890481/

3度目の紹介．自然基底が図形的に理解できます．おもしろい本です．

一般相対性理論 内山龍雄 裳華房 (絶版) 古典的なテンソル解析が網羅されているので，これをモダンな観点から再構成すると良い勉強になるのですが，絶版．

ほかによい本はなのでしょうかね． > yama様，MXK様

Joh さんのレス (2006/09/20(Wed) 23:52)

私が使っているのは，

Tensors, Differential Forms, and Variational Principles (David Lovelock & Hannno Rund: Dover)

です．まあまあ良い本だと思っています．

MXK さんのレス (2006/09/21(Thu) 00:10)

まずは，公式 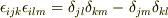をたよりに，ベクトル解析の公式をかたはしから証明してみてはどうでしょう．

MXK さんのレス (2006/09/21(Thu) 00:15)

本をおすすめできるほど，詳しくはありませんが，

包括的で安価なものとして

Bishop and Goldberg: Tensor analysis on manifolds (Dover)

Lovelock and Rund: Tensors, differential forms, and variational principles (Dover)

古いけれど，何だか迫力があるものとして，

Schouten: Tensor analysis for physicists (Dover) 絶版？

計算がフォローできて，何となく分かった気にさせるものとして，

Dirac: General theory of relativity (Wiley)

変わったやり方として，

数式処理ソフトMAXIMAなどで遊ぶのもいいかも知れません．

和佳 さんのレス (2006/09/21(Thu) 00:23)

> 一般相対性理論 内山龍雄 裳華房 (絶版) 古典的なテンソル解析が網羅されているので，これをモダンな観点から再構成すると良い勉強になるのですが，絶版．

工学部の分館だからなのか良くわかりませんが，図書館は相対論だけ異常なまでに手薄で，残念ながらありません（量子力学は化学の人たちが必要とするせいか，そこそこなんですが）． 内山龍雄「相対性理論」岩波書店，はまだ版を重ねているようですが，これはご覧になったことありますか？同じ著者なので極端に劣ることは無いと思いますが．

> Geometrical Vectors (Chicago Lectures in Physics) Gabriel Weinreich ::

> Tensors, Differential Forms, and Variational Principles (David Lovelock & Hannno Rund: Dover)

英語の本で勉強したことないので少し勇気要りますが，安いようなので近いうちに手に入れようかと思います．

和佳 さんのレス (2006/09/21(Thu) 00:29)

MXKさん，ありがとうございます． 洋書だと数え切れないほどありそうですね．

toorisugari no Hiro さんのレス (2006/09/21(Thu) 08:27)

>Dirac: General theory of relativity (Wiley)

は和訳が文庫

• http://www.amazon.co.jp/exec/obidos/ASIN/4480089500/

ででてますね．

ｙama さんのレス (2006/09/21(Thu) 09:18)

一般相対論の入門書としては，須藤靖「一般相対論入門」（日本評論社）があります．

• http://www.amazon.co.jp/gp/product/4535784221/sr=1-1/qid=1158796200/ref=sr_1_1/250-5662720-6421814?ie=UTF8&s=books

テンソルの変換則や共変微分については基底ベクトルを用いて説明されていますが，本論に入ると基底ベクトルは表に出さず，成分の計算に終始します． 本文中の詳しい計算が必要なところを練習問題に回してあるほか，本文の内容を補足・拡充するような問題もあるので，練習問題をきちんとやれば理解が深まるとともにかなり計算力が身につくと思います． 難しい問題もありますが詳しい解答がついています．

和佳 さんのレス (2006/09/21(Thu) 16:57)

ありがとうございます．どれも良さそうですね．お金がいくらあっても足りないくらいです．

toorisugari no Hiro さんのレス (2006/09/21(Thu) 18:25)

> 内山龍雄「相対性理論」岩波書店，はまだ版を重ねているようですが，これはご覧になったことありますか？同じ著者なので極端に劣ることは無いと思いますが．

昔読んだ記憶だけですので，まちがってるかもしれませんが，「数式をあまり使わず一般相対性理論を理解させる本」というふれこみだったような．

でも，文章が重くて挫折したと思います．

(訂正:これは新書の「相対性理論入門」の話でした．全書の「相対性理論」は挑発的な書き方の割に大したことない内容だったと思います．)

和佳 さんのレス (2006/09/21(Thu) 22:57)

> 全書の「相対性理論」は挑発的な書き方の割に大したことない内容だったと思います． なるほど．良い本を書いた人がいつも良い本を書けるとは限らないんですね．ありがとうございました．

MXK さんのレス (2006/09/21(Thu) 23:59)

toorisugari no Hiroさん，

>ああ，まだ，頭がcoordinate-dependentだった．．．．orz

そうなんですが，一方座標がなければ一歩も進まないことも事実で， 特定の座標系を特別視せず，すべての座標系を総体的に捉えることが 重要だと思います．「座標に依存しないベクトルの実態」といっても 何だかよく分からないものになってしまいますよね． 一旦，座標フリーであることの重要性が理解できた立場からは， >「物理法則は任意の運動をしているどんな座標系からみてもその数学的表現形式が同じである．」 は，結構いい表現に見えたりしませんか？

mNejiさん，

引退されるのはとても残念です．またどこかでお会いしたものです． 餞別に本を贈ります． www.amazon.co.jp/exec/obidos/ASIN/4121501713

mNeji さんのレス (2006/09/22(Fri) 01:04)

和佳さん：

若い時に，集中的に興味のある点を掘り下げるのは，とても身に付くと思います．と同時に，ちょっと第三者的な広い視野も確保すると良いですね．アドバイザリ・コミティの面々に揉んでもらうと素敵だと思います．ベストを尽くされますように．

MXKさん：

餞別戴きました．自分とは縁が無いことだろうと思いながら見てドキッとしました．私自身もその一人かもしれないからです(笑)．最近はLaTeXで単位を書くときに，グラムやメートルが出てくると異様に緊張するようになりました．啓蒙ご苦労様です．

toorisugari no Hiroさん，ｙamaさん：

解説をさせていただいて，とても勉強になりました．その刺激により，40年も前の友人達との論議が，こんなにリアルなイメージで出てくるとは，驚きでした．英語や数学では，落ちこぼれを自認していた自分が物理に追従できたのは，友人達のバックアップがあったのに今頃気づきました．この数式掲示板も似た効用が在りそうですし，なによりオープンな環境が素晴らしいのだとおもいます．

自分の性格は，物理に付いては，あくまで妥協せずにドライに追及したいので，裏返せば職人気質的にゆっくりと解説を書くのが生に合いそうです．ネット事情は第二変革期を向けているようなので，またどこかでお会いできたら楽しいとおもいます．失礼しました．

和佳 さんのレス (2006/09/22(Fri) 14:38)

> と同時に，ちょっと第三者的な広い視野も確保すると良いですね．アドバイザリ・コミティの面々に揉んでもらうと素敵だと思います．ベストを尽くされますように．

おっしゃるとおりだと思います．申し訳ありません．物理の根本になると（勝手に）思った数学に関してはかなり我侭だと思います．大学でも人格が変わるといわれました．後期にやることになっている複素関数や調和解析は物理的にはまだ計算の手段というイメージしか持ってないのでムキにならずに済みそうなんですが...． 今後気をつけたいと思います．

toorisugari no Hiro さんのレス (2006/09/22(Fri) 15:46)

mNejiさん これからもいろいろ議論したかったのですが，残念です． また，お会いすること楽しみにしています．

toorisugari no Hiro さんのレス (2006/09/22(Fri) 17:32)

> 「座標に依存しないベクトルの実態」といっても何だかよく分からないものになってしまいますよね．

(^^;) 「幾何学的な，『座標に依存しないベクトル』」ってあるのかといわれると微妙ですね．3次元ユークリッド空間あるいは 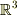の幾何というのは何だろうといつも考えています．

ただ，「共変な添え字体系」で理論が記述できるというより，「テンソル/ベクトル」というものが(何かはよくわからないが)「存在」して，それは我々には「共変な添え字体系」で認知するしかないものだが，本来自然現象は「テンソル」で記述されているのだ，と考える方が自分にはわかりやすいです． (あまりこだわるとあっちの方にいってしまうので自制は忘れませんが．．．．)

> 特定の座標系を特別視せず，すべての座標系を総体的に捉えることが重要だと思います．

ま，現実的にはこれが一番正しい態度ですね．

MXK さんのレス (2006/09/22(Fri) 21:13)

mNejiさん，

余談ながら，しかも時間ぎれかも知れませんが，

axb とかいう表記は 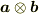のことです． 2つのベクトルから2階のテンソルを作る操作です．簡単にいえば 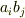を成分とする行列です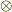． が一杯出てくると目障りなので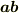， と省略されることが多いです． というわけで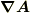， は 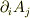を要素とする行列を表すことになります． この行列の対角和 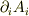が発散， 反対称化したもの が回転に 対応します．