えり さんの書込 (2006/09/10(Sun) 19:43)

こんにちは，高卒の受験生です．

質量Ｍの直方体がなめらかな水平面上におかれている．Ｍの上に置かれた質量Ｍ2の物体から水平にはったひもを滑車にかけ，その先端に質量Ｍ1の物体を鉛直に吊り下げる．Ｍ1の側面はＭと接し，上下になめらかにすべることはできるが，離れないような構造になっている．ただし，ひもはのびず，その質量は無視できる．また，ＭとＭ2の間には摩擦がなく，重力加速度はｇとする．

という問題で，ＭとＭ1の水平方向の運動方程式は右向きを正とし，抗力をR,張力をTとすると，

Ｍα=-R-T Ｍ1α=R

であっていますか？

yama さんのレス (2006/09/10(Sun) 20:48)

詳しい状況が分からないのですが・・・ 滑車は直方体の右上端に固定されているのでしょうか？ また，R は直方体から質量Ｍ1の物体にはたらいていて，右向きを正としているのですね？ その場合は，運動方程式はそれでいいと思います． ただし，R は負になると思われるので，抗力と呼ぶのが適切かどうかはちょっと疑問ですが．

mNeji さんのレス (2006/09/10(Sun) 21:05)

なにか図が浮かんできません．<PRE>と</PRE>で上下に挟んで書くと，書いたように表示できます．ただし「PRE」は小文字「pre」にしてください．

例えば ↓<PRE> <pre> +------+ | M2 +----------------------● +--------------+ ｜ | M | ｜ | | +---+ | | ? |M1 | | | +---+

</pre> ↑</PRE>

mNeji さんのレス (2006/09/10(Sun) 23:08)

クイズと思って無理やりに書いてみる．

滑車がMより出ていると考えるしかなさそうだ．

<pre>

+------+ →← | M2 +-------／●↓T | →β | ／ | +--------------+ | | | |↑T | →α |+------+ | M ← || M1 |→+R | -R |+------+

(M1 + M2)β = +M1g (M2)β = +T

(M + M1)α = -T (M1)α = +R

</pre>

＃このような問題を考えるヒトって，どんなヒトだろうか？ 不思議だ．

えり さんのレス (2006/09/11(Mon) 00:20)

>滑車は直方体の右上端に固定されているのでしょうか？ また，R は直方体から質量Ｍ1の物体にはたらいていて，右向きを正としているのですね？

そうです，本来はこの問題に図が書いてあったのですが，書き方がわからないので文だけになってしまいました．すみません・・・

＞ただし，R は負になると思われるので，抗力と呼ぶのが適切かどうかはちょっと疑問ですが．

これはどういう意味でしょうか・・・R<0であって，-R>0ということでしょうか・・・

＞このような問題を考えるヒトって，どんなヒトだろうか？ 不思議だ．

このような現象解析は，実際に役立たないということでしょうか？

mNeji さんのレス (2006/09/11(Mon) 01:18)

>このような現象解析は，実際に役立たないということでしょうか？

仮に，先に書いた絵があっているとして，そのような構造体が我々のしっている装置だとか，工事機械などに存在しますか？

私は，頭のトレーニングだと割り切って見ているので平然と解いて見ますが，自分が受験勉強だったら，こんな問題を出すところは受けません...，ちと言い過ぎかもしれませんが．

yama さんのレス (2006/09/11(Mon) 07:22)

>これはどういう意味でしょうか・・・R<0であって，-R>0ということでしょうか・・・

そういうことです．

>Ｍ1の側面はＭと接し，上下になめらかにすべることはできるが，離れないような構造になっている．

と書いてありますが，M1がMから離れないためには R<0 でないといけないからです．

従ってこの場合にはたらく力は「抗力」と呼ぶよりも，「拘束力」と呼ぶほうが適切かと思います．

Chappy さんのレス (2006/09/11(Mon) 10:47)

mNejiさん ＞仮に，先に書いた絵があっているとして，そのような構造体が我々のしっている装置だとか，工事機械などに ＞存在しますか？ ＞ ＞私は，頭のトレーニングだと割り切って見ているので平然と解いて見ますが，自分が受験勉強だったら， ＞こんな問題を出すところは受けません...，ちと言い過ぎかもしれませんが．

僕はどうしてもこういう問題はうきうきして解いてしまいますね (^^; とにかくおもしろそうなんです． 僕の場合，実用性より好奇心で解いていた気がします． その好奇心が純粋に物理法則に向けられればよかったのでしょうが．．

追伸：mNejiさんの図でいくと（僕もそうなると思います） と 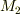の間に摩擦がないとつまらないですね．

mNeji さんのレス (2006/09/11(Mon) 13:02)

yamaさん： >と書いてありますが，M1がMから離れないためには R<0 でないといけないからです． > >従ってこの場合にはたらく力は「抗力」と呼ぶよりも，「拘束力」と呼ぶほうが適切かと思います．

いつも拝見していて思うのですが，とても繊細な「観察力と表現力」で感心するばかりです．自分も，図を書いているときにMとM1の表面で押し合うような感じにしたかったのですが，書ききれませんでした．

Chappyさん： >僕はどうしてもこういう問題はうきうきして解いてしまいますね

ああ，そうだったのか．えりさんの質問の傾向は，数学よりの物理なのかも知れませんね．

>追伸：mNejiさんの図でいくと（僕もそうなると思います）MとM_2の間に摩擦がないとつまらないですね．

強く同意．M2をクレーンの操縦席で，床とのキャタピラの摩擦力を考えるとか...(笑)．そう来るとM1は海底に沈んで...．

ｙama さんのレス (2006/09/11(Mon) 15:49)

>とても繊細な「観察力と表現力」で感心するばかりです．

抜けているところだらけなのに感心して頂いて恐縮です． 確かに，問題を理解するには観察力が必要だし，自分の考えを他の人に理解してもらうには文章の表現力が重要ですね．

えり さんのレス (2006/09/12(Tue) 00:37)

↓の表題を本来のものに変更しました．

この記事を削除しようとしましたが，管理側で削除すると問題がでそうなのでこのままにしておきます．

もしパスワードを設定してあれば，パスワードを使って，ご自分で削除できると思います． --mNeji, 2006-09-13, 14:56

えり さんのレス (2006/09/12(Tue) 00:39)

>Ｍ1の側面はＭと接し，上下になめらかにすべることはできるが，離れないような構造になっている．

と書いてありますが，M1がMから離れないためには R<0 でないといけないからです．

従ってこの場合にはたらく力は「抗力」と呼ぶよりも，「拘束力」と呼ぶほうが適切かと思います．

なるほど，拘束条件によってそのようになっているのですね！！よくわかりました，ありがとうございました．

そして皆さん，物理的な視点で物事を見れるってかっこいいですね！！私も早く数学でなく，物理の質問ができるようになりたいと思います．（先は険しいですが・・・）これからもよろしくお願いします．