ガウスの法則

A cubic box of side a = 0.280 m is placed so that its edges are parallel to the coordinate axes, as shown in the figure. There is NO net electric charge inside the box, but the space in and around the box is filled with a nonuniform electric field of the following form: E(x,y,z) = Kz j + Ky k, where K = 4.50 N/(Cm) is a constant.

What is the electric flux through the top face of the box? (The top face of the box is the face where z = a. Remember that we define positive flux pointing out of the box.)

What is the total electric flux through the five other faces of the box? (Again, outward flux is positive.)

Re: ガウスの法則

ｙama さんのレス (2006/09/12(Tue) 10:29)

「電界」も「電場」も「electlic field」の訳語ですが，電気工学では「電界」，物理では「電場」が用いられることが多いようです．学習指導要領では「電界」が使われているため，高校物理の教科書では「電界」が使われていましたが，最近では「電場」も多く使われるようです．「電場束」という語は初めて見ましたが，「electric flux」の訳語として辞書に載っているのでしょうか？普通は「電束」といいます．

問題について説明しておきます．電束の定義は教科書に書いてあると思いますが，面に垂直な電束密度の成分を，その面上で面積分したものです．面に平行な成分は電束の値に寄与しないので考慮する必要はありません．

2)についてはガウスの法則を利用します．ガウスの法則については，教科書をよく読んでください．ガウスの法則を用いれば，立方体の６面全体を通る電束が簡単に求まります．その値から 1)で求めた電束の値を差し引いたものが，残り５面を通る電束です．

3)もガウスの法則を用いて求められます．

私ははじめ Kz をKのz成分と考えたため，問題の意味がよく分かりませんでしたが，よく考えてみると，K×z のようですね．

Re: ガウスの法則

Chippy さんのレス (2006/09/12(Tue) 11:55)

yamaさん本当に有難うございました．

∫4.5y(dA)= ∫∫4.5(dy)(dx) = 2.25(y^2)(x)=(2.25)(0.28^2)(0.28)

= 0.494Ｎｍ^2/Ｃ（定積分の範囲の記入は省略して書いています）

（２）も同じように解いたところ−0.494Ｎｍ^2/Ｃとなりました．

皆さんの御協力とても心から感謝しています．本当に有難うございます．

余談ですが，アメリカ人が理数系が苦手な方が多いのは，教科書の判り難さや，日本の様に指導力が高い教員が少ないからだと思います．生徒の質問を受け付けない教授や解答ものっていない教科書には本当にあきれます．異国に来て日本は教育の指導レベルに関しては先進国だと感じます．

Re: ガウスの法則

ｙama さんのレス (2006/09/12(Tue) 13:15)

電束密度 D=εE なので誘電率を掛けないといけません．

大学の教科書は，アメリカのほうが詳しく丁寧に書いてあるように思うのですが，問題の解答がほとんど載っていないのは困りますね．

Re: ガウスの法則

mNeji さんのレス (2006/09/12(Tue) 13:37)

>ベクトル解析の本は持っておりません，また高校レベルのベクトル知識しかありません．

とても失礼な言い方になるかもしれませんが，このようなナイーブな考え方は捨てた方が良いと思います．

最近の質疑応答をフォローしてまいりましたが，物理の問題として理解できないというよりは，数学の理解がないままに，細かな問題を一つ一つとかれても，一寸毛色の違う問題で止まられているように思います．

たしかに，それまでの問題が，電荷密度の分布対称性を元にした積分型の典型でしたが，それにしても面積分の考え方が確りしていないと，幾ら問題数をふやしても，理解の向上が得られないとおもいます．

米国の大学のカリキュラムも，またどんな学部でのどのような講義かにもよるとはおもいます．が，米国で現在,9月，新学期そうそうの時点で，ガウスの微分形，積分形が問題になっているということは，少なくとも昨年から講義を受けたのでは無いかと推察します．

その授業で，ベクトル解析がわからなければ，緊急に日本の解説書を購入して，勉強しないと駄目だろうと思います．

私は，米国で勉強した経験はありませんが，何回か米国人と接した経験があります．物理とか電気化学の関係の話でした．その経験を示します．

米国人は，「人種」と「その人の能力」そして「趣味・学歴」すらを，とても目ざとく察知します．従って，質問する場合は，とても注意を要します．例えば，積分と申しましても，体積分，面積分，線積分とありますね．物理の問題を論議する前に，このような論議をスパッ理解して質問できないと，その時点で，説明を求められた方は「不勉強な人だから，適当に対応しよう」といった態度になります．

面白い事に，質問を受ける方が高いポジションに付いている場合，部下を使って，やんわりと事前知識を教えるようにしてから，本題を解決してくれることも在ります．

＃偉い人は，それなりに，この質問者はどの程度教えれば問題を＃クリアできるかを見定めています．＃＃ですから「ここまでは判るが」，「この過程から先が判らなくなる」と，＃相手に，考えるヒントを混ぜて論議するのも有効です．＃＃逆に，あいてがあまり偉くない場合，細かな配慮をする能力が＃少ないので，次に述べる正攻法でアタックしましょう．

ですから，物理の問題を質問する場合，事前的な数学はクリアしましょう．このサイトには物理数学をとても流暢に解説する天才や，図形問題をするりと解決できる数学の猛者もいらっしゃいます．勿論，物理の数学としてもｙamaさんらの名解説をいただけるとおもいます．

なお，私は何十年も前に学生だったのでよいベクトル解析や電磁気学の本とかを存じません．必要なら，ここで質問されるようにするのはお勧めです．

また，用語の事ですが，日本では高校と大学で違う用語を使っているのを知って，とても驚いています．もし，物理系の学科で，今後とも日米で勉学・研究・仕事をされるお積りならば；・岩波理化学辞典第4版

を手元に置かれているとよいと思います．

ちなみに

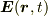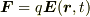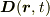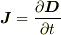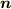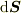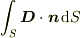・電場=(電界)='electric field" 例： $\bm{E}(\bm r,t)$ ・電気力="electric force" 例：電荷qを持つ物体が，電場の中で受ける電気力は $\bm F = q\bm{E}(\bm r,t)$ ・電束密度="electric flux density" 例： $\bm{D}(\bm r,t)$ 例：コンデンサに時間に伴う電位が掛けられて，交流の電流が電極に流入する．そのときに電極間に流れる変位電流(displacement crrent)は $\bm J = \frac{\partial \bm D}{\partial t}$ ・電束密度="electric flux" 例：ある曲面の法線方向 $\bm{n}$ にむいた微小面積素 $\mathrm{d}\bm{S}$ と電束密度との内積を曲面について加えたものを電束と呼ぶ：例： $\int_{S}\bm{D}\cdot\bm{n}\mspace{2mu}{\rm d}S$ ・誘電率="dielectric constant" 例：通常 $\varepsilon$ と書き， $\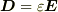bm D = \varepsilon \bm E$

＝＝＝＝

・なんといっても異国の地で勉学するのは，文章にしがたい難しさがあると思います．・でも，米国人はある意味，西洋とか東洋の歴史に強いコンプレックスをもっているのも事実です．・ですから，日本古来の事について薀蓄をもつとか，古武道の力学的分析をするなどをやれると，彼等は貴方のことを尊敬すらします．一例ですが．・あと，ひょっとして，会話が流暢すぎて，発言が含蓄に富みすぎているのは絶対にさけるべきとおもいます．英語のうまい人と2人で会議に出たとき，

＃その人が「英語は明らかに自分の方が上なのに，＃意思疎通の量は貴方に勝てない」，なんで？

といわれました．そのご，米国人にこの点をきいたら，

＃あんたの話し方は「ストロング・アーギュメント」なので＃理解しやすい．むしろ英語が綺麗なのに論理が弱いと聞く気にならない．＃＃また発音が目茶目茶だが「語彙を替えてくる」ので＃複数の単語を聞いているうちに何が言いたい単語がわかるのだ

といわれました．某大先生にも，

＃発音というより，イントネーションに注意し，＃イントネーションの無いところは，発音を口ごもってしまえ！

といわれました．

逆に言えば，英語が巧過ぎるすぎる人は「ぶっきらぼうで強い表現をする」方が良いかも知れません．

いずれにしろ，ベストを尽くされますように！

Re: ガウスの法則

mNeji さんのレス (2006/09/12(Tue) 17:34)

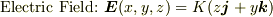
目を通して論議を定着させる為に，図を描いてみます． <pre> $\text{Electric Field:}\ \bm{E}(x,y,z) = K(z \bm{j} + y \bm{k})$

$+z: \bm{k}$

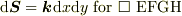｜｜ $\mathrm{d}\bm{S}=\bm{k}\mathrm{d}x\mathrm{d}y \ \text{for}\ \square \ \text{EFGH}$ ｜↑ E(0,0,a)｜＿＿＿＿｜＿＿＿＿ F(0,a,a) ／｜＿｜／｜／｜／＿／／｜／｜／｜／｜／｜／｜／｜

H(a,0,a)／＿＿＿＿＿＿＿＿／｜

｜｜｜G(a,a,a) ｜｜ A(0,0,0)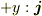｜＿＿｜＿＿＿＿＿＿｜＿＿＿＿ $+y: \bm{j}$ ｜／｜／ B(0,a,0) ｜／｜／｜／｜／｜／｜／｜／｜／

｜＿＿＿＿＿＿＿＿＿｜／

／ D(a,0,0) C(a,a,0) ／

$+x: \bm{i}$

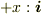
</pre>

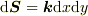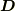【A1】図中の，正方形EFGHの面について，zの正の方向に向いた微小面ベクトル $\mathrm{d}\bm{S}=\bm{k}\mathrm{d}x\mathrm{d}y$ と電束密度 $\bm D$ との内積の総和で求められる．

なお，この立方体の誘電率 $\varepsilon$ とすれば，

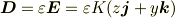
$\bm D = \varepsilon\bm E= \varepsilon K(z \bm{j} + y \bm{k})$

従って面EFGHを+zの方向に通過する電束は；

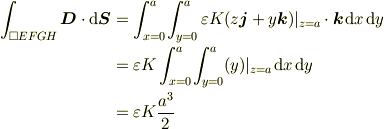
$\int_{\square EFGH}\bm{D}\cdot\mathrm{d}\bm{S}&= \int_{x=0}^{a}\mspace{-1mu}\int_{y=0}^{a}\varepsilon K(z \bm{j} + y \bm{k})|_{z=a}\cdot\bm{k}\mspace{2mu}{\rm d}x\mspace{2mu}{\rm d}y \\&= \varepsilon K\int_{x=0}^{a}\mspace{-1mu}\int_{y=0}^{a}(y)|_{z=a}\mspace{2mu}{\rm d}x\mspace{2mu}{\rm d} y \\&= \varepsilon K\frac{a^3}{2}$

まあ，一度は清書して見ると，指と目から記憶が強化されますね．

色々な経験が出来るのだから，楽しくベストを尽くされるように．

Re: ガウスの法則

CO さんのレス (2006/09/13(Wed) 16:42)

> mNeji さん

ASCII アートをずいぶんキレイに書かれますね． :) なにかツールなど使用していらっしゃるのでしょうか？

Re: ガウスの法則

mNeji さんのレス (2006/09/13(Wed) 17:32)

>なにかツールなど使用

ただただ慣れです．こつは大雑把に書くことです．書いてるうちに，図のほうがこうしてくれと言い出します．

もう一つは，ASCII アートは馬鹿げてると思っていたのですが，デジタル・アートの元祖だと思うようになりました．最近はInkscapeで好きなだけ書けてしまう反動かもしれませんね．

文章・数式・グラフィックスが一つのアプリケーションで自在に書けるのに，あと何年まつのかなぁ．

そういえば，保存版だと<Pre></Pre>が崩れますが，LaTeXで処理はできませんか？

Re: ガウスの法則

CO さんのレス (2006/09/14(Thu) 00:43)

> そういえば，保存版だと<Pre></Pre>が崩れますが，LaTeXで処理はできませんか？

LaTeX で処理せずとも対応できます．時間の出来たときに対応しておきます． :)

Re: ガウスの法則

mNeji さんのレス (2006/09/14(Thu) 02:12)

COさん：

なるほど了解いたしました．よろしくお願い申し上げます．

こんご，アスキー・アートも利用する方も安心されますね．

＝＝＝＝＝＝＝

Chippyさん：

近くのスレッドで電束の面積分の表現について，識者の方々からの助言を受けて修正しました．参考になれば幸いです．

"手に馴染むLaTeXe #01 mNeji - 2006/08/20(Sun) 01:10 No.11396"

http://hooktail.maxwell.jp/cgi-bin/yybbs/yybbs.cgi?room=room1&mode=res&no=11396&mode2=preview_pc

Re: ガウスの法則

Chippy さんのレス (2006/09/16(Sat) 22:32)

mNejiさん詳しい解説をいただきましてありがとうございます．

先学期にとった物理Iは力学（日本の高校の範囲が主）でしたが，今学期の物理IIは電気関係がメインになっているようです．大体高校の物理IIがメインとなると聞いていたんですが，この大学はいささか違うようです．．．授業開始→クーロン→一週間で→ガウスの法則

現地の学生は先日の物理の実験のときにオームの記号も知らなかったので，恐らくまだ電気関連について何も習っていないのだと推測します．にもかかわらず初っ端からガウスの法則ですから，日本では考えられない教授です．

私は高校のときは物理Iまでしか履修していなかったので，今かなり苦しんでおりますが，可能な限り努力しようと強く思います．授業も進むのがかなり速く，解説も貧しい時なども多々ありますそんなときにわからない問題があった時に，皆さんのご指導を頂けましたらとてもうれしく思います．

mNejiさんの異文化コミュニケーションに関するお話強く共感いたします．

Re: ガウスの法則

mNeji さんのレス (2006/09/16(Sat) 23:33)

Chippyさん：

状況は重々承知しました．この数学掲示板を見ている多くの方が，Chippyさんを応援しているとおもいます．

回答者の方々のことも考えると，日本語の参考書を取り揃えて置くのもいい方法と思えます．(逆に日本人の学生は，下手な教官の授業を馬鹿にして洋書で勉強することも多々ありました)

その為には，カリキュラムが判れば，先行的に公開して，前もって日本語の教科書を先行手配したり，先行勉強して，事前に質問を此処に書いておく等の工夫も出来ますね．

また少数でいいですから気心のあう友人が出来ると良いですね．エンジョイ，物理！

Re: ガウスの法則

Chippy さんのレス (2006/09/17(Sun) 08:23)

ｍNejiさん，ありがとうございます，とてもうれしく思います．

以前の大学の先輩方から物理IIの内容を事前に聞いて，日本で参考書（高校レベル）を買い揃えて持って来ましたが，やはりアメリカは州を越えるとそれは通用しない様ですね．そして今使っている教科書は図解説が乏しく，イメージとして出来事を捉えるのがとても難しいです．今学期は力学，材料工学，Multivariable Calculus，英文II，そして物理IIをとっておりどの教科もかなり大変で時間も制限されてますが，私なりに物理も何とか頑張りたいと思います．

回答者の方々にアドバイスをいただける為にも，自分なりにネットなどで情報を集めます（たまに日本語サイトが文字化けして読めないこともありますが）

Re: ガウスの法則

mNeji さんのレス (2006/09/17(Sun) 11:53)

Chippyさん：

私は，年寄りですが，若い頃は好き勝手に物理を勉強してきたと思ってきました．ところがこの1週間ほど，中学生から以降の記憶をたどっていくと，とても良質な友人に支えられていた事をしりました．大変驚愕しています．

学問に限った事ではないでしょうが，切磋琢磨するのは当然ですが，友人と相互に支えあうことの楽しみや・面白みもぜひ経験していただければとおもいます．

私自身は，どんな場所でも，頑固に自分の方法で物事に対処してきました．が，こちらの数式掲示板で多くの回答者の方々の回答を拝見したり，間違った回答をご指摘されてギャフンとなったり，とても刺激的な経験を楽しませていただいています．

Chippyさんの最初の頃の質問は，「おふざけ質問」かと思い回答をためらいました．でも．今では皆さん，Chippyさんの質問に回答していただけると思います. 質問を和訳する時間が苦しければ，とりあえず英語の質問を完全な形でだしてしまっても良いとおもいます．

そのかわり，理解された結果は，克明に書き込まれると良いと思います．むしろレポートに書くように(英語も可)書けば，回答者も，最終確認ができます．さらに，横から問題を見ている方々にも判り易いとおもいます．

ちょっとキザナ言い方をすれば，インターネット越しに，物理を魚にした知的友情のリンクを作っていきましょう，と言うことだと思います．軽いフットワークで楽しみましょう．

[home] [掲示板] [ページの先頭]