単振動の運動方程式の解法について

単振動の運動方程式の解法について

ゆう さんの書込 (2006/09/05(Tue) 00:27)

単振動の運動方程式の解法について

こんばんは． 先日はありがとうございました．

今回は単振動の問題なのですが バネと質点が吊り下げられており，鉛直下方に 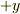+y 軸を取り， k をバネ定数とすると 運動方程式は以下のようになると思います．

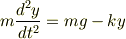
m\frac{d^2y}{dt^2} = mg - ky

この運動方程式を解いて，速度の式と位置の式を導こうと考え，式を変形しました．

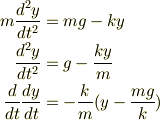
m\frac{d^2y}{dt^2} &= mg - ky \\\frac{d^2y}{dt^2} &= g - \frac{ky}{m} \\\frac{d}{dt}\frac{dy}{dt} &= -\frac{k}{m}(y - \frac{mg}{k})

空気抵抗のある落下運動などは，ここで変数分離をして解くのだと思うのですが この場合線形２階微分方程式というものみたいなのですがちょっと解き方が分からなくて．．． バネなので最終的な答えはcosもしくはsinの形になると思うのですが，どうしてもこの式からsin，cosの形になるのがイメージできなくて． 以上よろしくお願いします．

Re:単振動の運動方程式の解法について

tadash さんのレス (2006/09/05(Tue) 01:15)

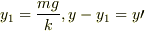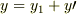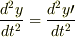ゆうさん，はじめまして ゆうさんが変形された最後の式で， y_1=\frac{mg}{k},y-y_1=y\prime とおいて y=y_1+y\prime とさらに変形します． すると \frac{d^{2}y}{dt^{2}}=\frac{d^{2}y\prime}{dt^{2}} と表され， 結果，

\frac{d^{2}y\prime}{dt^{2}}+\omega^2y\prime=0,\omega=\sqrt[]{\mathstrut\frac{k}{m}}

と斉次方程式に帰着して解くのがいいのでは？ この方程式は 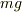mg という項が加わったために非斉次方程式になっているので，非斉次方程式の解き方に従うのもいいかと．