えり さんの書込 (2006/09/04(Mon) 23:48)

こんにちは，高卒の受験生です．以下の問題の解説を読んでいて理解ができないところがあったので，質問させていただきました．

「水平面とのなす角がθの斜面がある．（図のように，）最大傾斜の方向上向きを正とするy軸をとり，これに直交する水平方向右向きを正とするx軸を設定する．いま，原点Ｏに質量Ｍの小物体をおくと，小物体は静止したままであった． この状態から小物体に，+y方向に対して角度αの向きに斜面に沿って力を加えて次第に大きくしていくと，この力の大きさがＦになったとき，小物体は動き始めた．重力加速度をｇ，小物体と斜面との静止摩擦係数をμ，動摩擦係数をμ’（μ＞μ’）とする．

(4)小物体が動きはじめた後も，常に角αの向きに(3)で求めた力Ｆを加え続けた．動き出してから距離Lだけ移動した瞬間の小物体の速さをμ，μ’，θ，ｇ，Lで表せ．」

という問題で，

「動き出す直前のつりあいより，ＦとＭｇsinθの合力は，ベクトル和の向きにμＭｇcosθである．この方向に滑り出した直後から摩擦力はこれと反対向きにμ’Ｍｇcosθとなる．」

という解説があるのですが，なぜ動き出したら摩擦力の向きが反対になるのかがわかりません．教えてください，おねがいします．

yama さんのレス (2006/09/05(Tue) 00:23)

摩擦力の向きが反対になるわけではありません． 動き出す直前には，摩擦力は，ＦとＭｇsinθの合力とつりあっています． つりあっているので，摩擦力の向きは，合力と反対向きです． 滑り出した直後の摩擦力もこれ（合力）と反対向きです． つまり滑り出す前も後も，摩擦力は合力と反対向きであって，向きは変わりません． 静止摩擦力が動摩擦力に変わるだけです．

えり さんのレス (2006/09/06(Wed) 23:55)

返信遅れて申し訳ありません．

向きは変わらないとのことでしたが，なぜ運動方程式を立てる際に Ｍα=μＭｇcosθ−μ’Ｍｇcosθ のように，摩擦力の符号が変わるのでしょうか？

mNeji さんのレス (2006/09/07(Thu) 01:35)

横から失礼します．

なにか二重に話が混線してませんか．

1. 傾斜角について

・水平面とのなす角がθの斜面がある． ・最大傾斜の方向上向きを正とするy軸 ・+y方向に対して角度αの向きに斜面に沿って力を加えて

以上をあわせると，見かけの傾斜角φとすると sin(φ) = cos(α)sin(θ) として傾斜角を考える必要がありませんか．

2. 力Fについて．

1. +y方向に対して角度αの向きに斜面に沿って力を加えて次第に大きくしていくと，この力の大きさがＦになったとき，小物体は動き始めた．
2. (4)小物体が動きはじめた後も，常に角αの向きに(3)で求めた力Ｆを加え続けた．

少なくとも，a)より

F = μＭｇcos(φ)

この力を，そのままの角度で加え続けた場合，y軸からα傾いた方向の加速度をAとでもすれば，b)により

MA = F - μ’Ｍｇcos(φ) = μＭｇcos(φ) - μ’Ｍｇcos(φ)

ーーーーーー となっているように思いますが？

ｙama さんのレス (2006/09/07(Thu) 11:11)

見かけの傾斜角φを考える必要はないと思います． 面からはたらく垂直抗力は Ｍgcosθ であって，Ｍgcosφ ではありません． 従って摩擦力の大きさも μＭgcosθ（または μ'Ｍgcosθ）であって，μＭgcosφ（または μ'Ｍgcosφ）ではありません． また，この座標のとりかたでは，ｙ方向に -Mgsinθ の力がはたらくことになります． 問題を解く過程で cosαsinθ を含む項が出てくることはあるかもしれませんが，それを sinφで置き換える必要はなく，そのまま計算すればいいと思います．

また，動き出す直前の釣り合いの式 F = μＭｇcos(φ) もおかしいと思います． α=0 の場合を考えると，この式は F = μＭｇcosθ となります． しかし加えた力以外に重力（の斜面に平行な成分）-Ｍgsinθ がはたらくので，釣り合いの式は F-Ｍgsinθ = μＭｇcosθ になるはずです． α=0 でない場合は左辺は α（とθ）を含む式になりますが，右辺はそのままです．（摩擦力の向きは変わりますが大きさは同じです．） この左辺が「ＦとＭｇsinθの合力」であり，釣り合いの式は，その合力が μＭｇcosθ であることを意味しています．

つまり，運動方程式 Ｍα=μＭｇcosθ−μ’Ｍｇcosθ の右辺第１項は，ＦとＭｇsinθの合力であって，摩擦力ではないということです．第２項の動摩擦力と符号が反対になっていてもおかしくはありません．

mNeji さんのレス (2006/09/07(Thu) 11:13)

追加です．

「ある物体に力Fを加えても動かない」という事を，力の加える方向を+どんな風に考えるかというと； <pre>

物体：質量：M, 静止摩擦係数：μ' 重力加速度：g 地面 推進力：F→ ______↓______________________■____________________→ +xの方向 ← D：地面からの抗力

</pre>

これを式で書けば,結構面倒になります．

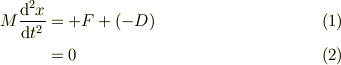
ここで,抗力については

要は，静止摩擦係数で決まる最大摩擦力までは，抗力は推進力Fに追従していつでもバランスします．

＃摩擦面を通して，物体のそこの分子や凸凹が，地面の分子や凸凹と， ＃莫大な数の衝突を引き起こして力の統計的なバランスを達成している ＃訳ですから人知を超えた現象とも思えます．

＃ですから，接触面積が小さくなった場合の現象は， ＃とても不思議な振る舞いをするようです．

実際は面倒だから，静止の式は，ムニャムニャにするのだと思います．

もちろん，押す部分を高くしすぎると，抗力がまだ頑張れるよりも先に，転倒してしまうことは注意しましょう．

＝＝＝＝＝＝＝

私が高校生の時にも「摩擦の現象」はとても不思議に思いました．上に書いた説明は，大学に入って「とてもクールな友人とビリヤードに凝った」時に，象牙球がフェルトの台を滑る場合と滑らない場合とがあるので，静止摩擦をどう考えるか喧々諤々して，上に示したような結論に達しました．

久しぶりに，「見かけの傾斜」などの話をしていて，その後に，ビリヤードの事を思い出したので，書いてみました．

えりさんのいくつかの質問は，多くの人が見過ごしてしまうような，でも結構大切な要点を自分の目で捉えていると思います．受験勉強の重圧のなかでも，「その目線」は大切にして，どんどん成長させてください．

えり さんのレス (2006/09/10(Sun) 17:48)

ちゃんと理解できました．mNejiさん，yamaさん，どうもありがとうございました．

mNeji さんのレス (2006/09/10(Sun) 20:48)

あっ．間違えてますね，ご両名さま，御免なさい．

どうも，ｙamaさんのNo.11757と自分の2番目の」発言が時間的に接近していたので，このご発言をいま知りました．

自分の最初の発言は；

自転車で急斜面を上がる時，きつければ斜めに動くことをイメージして 図を描いて，眠気にまけて，直ぐに投稿したためです．

運動と自転車が密接にイメージされているので，面の摩擦と車輪の摩擦の違いが直ぐに出てきませんでした(泣)．テストの時は，この違いを即座に確認してくださいね，と誤魔化す(笑)．