抵抗項の係数

抵抗項の係数

山旅人 さんの書込 (2006/09/02(Sat) 22:53)

本掲示板の最近の書き込みを見ていて気がつきました．速さに比例，速さの２乗に比例する抵抗の項の係数についてです．

と書かれており，いずれも抵抗項の係数に質量 m が現れています． 私は，このような記述を見慣れていなかったため，やや違和感がありました．

例えば本サイトの中にある

では，質量 m がありません．

どちらかが正しい・誤りということではなく，それぞれに一長一短があると思うのですが，皆様のご意見をお聞かせください．

Re: 抵抗項の係数

mNeji さんのレス (2006/09/02(Sat) 23:52)

私は，水泳の運動を解析しようとしています．水中の場合，水の抗力はv^2が主なようですが，解析が楽になるためにv^1で計算しています．

いずれの場合も，体重mは抵抗の係数には入れていません．そんな状況は考えられないからです．

空気中のボールの運動のご質問に付いては，上の意味で抵抗力にmが入るのは考えられないと思い，回答を差し控えました．

他方，今日の質問で，v^2がありましたが，正解として間違った答えでお困りのようだったのであえて回答させて戴きました． 朝，出かけでしたのであわてて回答をさせていただきました．もし時間があったら，回答をしなかった可能性が高いとおもいます．

逆に，「一長一短」とはどんな場合を想定されているか，お教えくださいますか？

Re: 抵抗項の係数

yama さんのレス (2006/09/03(Sun) 10:57)

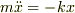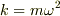係数に m をつけるのは，単に便宜上のことだと思います． たとえば，単振動の方程式 m\ddot x=-kx の場合，定数 k は普通は m に関係しないと思います． しかし， k=m\omega^2 と置くことによって m が消えて後の計算が簡単になります．もちろん，m が消えるのは見かけ上のことで，実質的には \omega の中に含まれているわけです．

抵抗係数の場合も同様で，係数を mk と置くのは，方程式から見かけ上 m を消すためだと思います．この場合，一般に k は m の関数になります． 当然，運動方程式の解も m を含まない形になりますが，もちろんこれは物体が質量に無関係に同じ運動をするということではなく，運動は k を通じて質量に関係することになります．

ただし，係数を初めから mk と書くと，係数が m に比例する（従って抵抗力が m に比例する）と誤解されるおそれがありますね． 初めは係数を k として，計算の過程で k=mγ などと置きかえたほうがいいと思います．

Re: 抵抗項の係数

山旅人 さんのレス (2006/09/04(Mon) 22:32)

yama さん，mNeji さん，コメント有難うございます．

私自身，「単に便宜上のこと」 で良いと思います． ただ，方程式の数学的な処理に熟練した方にはそれでよくても，学習半ばの方々にとっては，ご指摘のような，

> ただし，係数を初めから mk と書くと，係数が m に比例する（従って抵抗力が m に比例する）と誤解されるおそれがある

こと，さらに，「方程式から見かけ上 m を消」 したため 「k が m の関数になり」，すなわち，（逆に） k の中に m についての情報が隠されてしまったこと，にお気づきになるかが，老爺心ながら心配です．

その意味で，上に引用した本サイトの解説は，初心者に親切だと思います． ゆうさん，黒霧さん，おわかりでしょうか．