お願いします.
お願いします.
受験生 さんの書込 (2006/08/29(Tue) 14:29)
はじめまして. 入試問題を解いていたのですが解説がどーしても理解できなかったのでよかったらお知恵をいただけないでしょうか.
波の式y=A sin 2Π(t/T − x/λ)が与えられていて,この波ともう1つの波を重ねると定常波ができるそうです.でそのもう1つの波がy=Acos 2Π(t/T + x/λ)であるというのですが,なぜcosになるかがわかりません.同位相,同波長,で進行方向が逆で定常波は生じるのではないのでしょうか? 私はy=Asin 2Π(t/T + x/λ)だと思うのですが・・・.
Re: お願いします.
篠原 さんのレス (2006/08/29(Tue) 18:35)
はじめまして. 篠原です.
sinとcosで混乱されているようですが,波を考える場合,この二つに本質的な違いはありません.
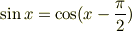
ですからね. 定常波のできる位置が少し変わります.
Re: お願いします.
山旅人 さんのレス (2006/08/29(Tue) 21:49)
篠原さん,山旅人です.上の式, sinx=cos(π/2−x)(cosx=sin(π/2−x) と書く方が better ですが) です.質問者が混乱すると思いますので,修正してください.その後,この投稿も削除します.
Re: お願いします.
やかん さんのレス (2006/08/29(Tue) 21:54)
みなさん,こんにちは. なるほど,反対向きの波に位相差があっても定常波ができるんですね. 勉強になりました.
Re: お願いします.
篠原 さんのレス (2006/08/29(Tue) 22:29)
みなさん,こんばんは.
>山旅人さん
>sinx=cos(π/2−x)(cosx=sin(π/2−x) と書く方が better ですが) >です.質問者が混乱すると思いますので,修正してください.
単なる表記の違いですよね. こちらの表現のほうが良いという根拠を教えてください. 併記するのなら分かりますが,「こっちの表現のほうがいいから変更したほうが良い!」とする理由が分かりません.
私は,sinとcosで,関数を単に平行移動しただけの違いであることを示したかったため,上記の表記を用いました.
上式を消し,修正しなければならない理由が分かりません. この点について,説明いただけたら幸いです.
# cosの中身が分かりにくいため,括弧はつけました.
Re: お願いします.
toorisugari no Hiro さんのレス (2006/08/29(Tue) 23:00)
受験生さんへ
境界条件(どこに節ができるかという条件)はどうなっていますか? それによってどのような波を重ね合わせるかは変わってきます.
Re: お願いします.
山旅人 さんのレス (2006/08/30(Wed) 00:04)
>> 篠原さん 書き換えを促したのは,当初の篠原さんの記述 sinx=cosx−π/2 が,<b>誤り</b> だからです.()はこの場合必須のものであって,見やすくするためにつけるものではないでしょう.
> (cosx=sin(π/2−x) と書く方が better )
と書いたのは,質問者が高校生だからです. 高校の教科書にある波動の一般式は,y=Asin2π(t/T−x/λ) と sin で与えられています.大学生とっては > sinとcosで,関数を単に平行移動しただけの違い であっても,高校生にとっては,そこで受ける印象の違いは大きいものです.で,このスレッドのような質問が生まれるのです.すなわち,<b>cos も sin から誘導できる同じもの</b> としたほうが高校生は理解しやすいのです.better と書いた所以です. この一般式も,もはや現在の教科書にはないようですが…
Re: お願いします.
篠原 さんのレス (2006/08/30(Wed) 00:12)
山旅人さん,ご指摘ありがとうございます. 括弧に関しての表記については,認めます. しかし,私の質問は,
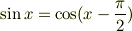
ではなく,
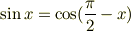
としたほうが良いという根拠は何ですか? ということです.
前者の場合,関数の単なる平行移動ですが,後者の場合は平行移動に加え,対称操作が加わるため,少しややこしくなると考えました. にもかかわらず,前者ではなく後者に書き直さなければならない理由を教えてください.
Re: お願いします.
山旅人 さんのレス (2006/08/30(Wed) 06:42)
> sinx=cos(π/2−x) とした方が良いという根拠 現在,高校生の多くは,一般角の三角関数になかなか習熟していないものです.sim,cos は三角形の中にある生徒が多いのです.そこで,sin30゜=cos(90゜−30゜) 等であることから(弧度法も未習熟の生徒が多いです),上記のように書きました. しかしながら,cos は偶関数ですし,ご指摘のような 「対象操作」 の難度もあることから,cos(π/2−x) <b>の方がよい</b> とは必ずしもいえないかもしれません.
Re: お願いします.
篠原 さんのレス (2006/08/30(Wed) 07:13)
山旅人さん,
理由も書かれずに,ただ「修正してください」とありましたから,後者の記述のほうが明らかに良いという根拠をお持ちかと思い,お尋ねしました. しかし,そのようではないようですね.
括弧以外の表記の違いについては,議論しても仕方なさそうですね. 投稿者の質問内容とは直接関係ないので,そろそろ止めましょうか...
表記に関するご指摘,ありがとうございました.
Re: お願いします.
komagatake さんのレス (2006/08/30(Wed) 12:27)
高校生で受験生でしたら三角関数はかなり習っていると思います.せっかく習っているのだから物理で使ってみると良いと思うのですが.高校では意外とやっていないと思います.蛇足かもしれませんが参考までに.
定常波でもうなりでも波の重ね合わせです.sinとsinの足し算は知っていますね.sinとcosの場合はπ/2ずらしたものを使えばいいです.質問の中の式を使います. sin2π(t/T−x/λ)+sin2π(t/T+x/λ)=2sin2π(t/T))・cos2π(x/λ) これは動かない波です.前が振幅の時間変化です.後ろが空間的な変位を表します. sin+cosも同じようにしてやればtとxとが分離された式が得られますので動かない波ということが分かるはずです.