ベクトル解析　流体力学

いちさんの書込 (2006/08/29(Tue) 10:52)

流体力学を勉強していたら運動量保存則の証明で ∫（−∇・（uρu))dV という式が出てきました（uはベクトル，ρはスカラーです）この（uρu)というのがわかりません．間に・も×もなくただuとρuを並べただけの演算ってありましたでしょうか？

前後の流れから推測すると u(∇・ρu)=∇・（uρu) となるようなのですが，これでは左辺はベクトルで右辺はスカラーになってしまいますよね，なにか根本的に勘違いをしているのでしょうか？

どなたかわかる方がいれば教えていただきたいです．よろしくお願いします

Re: ベクトル解析　流体力学

mNeji さんのレス (2006/08/29(Tue) 13:08)

始めまして．

私も，流体力学の勉強をするはずが，すこし横道に逸れている者です．流体力学は，オイラー表現，ラグランジェ表現と，方程式に行く前に，表現が難しく，さらに積分形式と微分形式を電磁気以上にスムーズに理解しないといけないので，気が休めませんね.

さて，流体の運動量 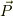$\vec P$ を考えると，固体と違って，ある領域について考える必要がありますね；

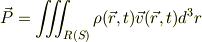
$\vec P =\int\mspace{-11mu} \int\mspace{-11mu} \int_{R(S)} \rho(\vec r,t)\vec v(\vec r,t)d^{3}r$

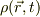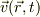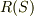此処で $\rho(\vec r,t)$ は密度，流体の速度を $\vec v(\vec r,t)$ とし， R(S) は表面Sで包み込まれた領域Rを意味し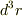， $d^{3}r$ は位置ヴェクタ 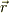$\vec r$ の近傍の微小体積を意味することとします．

何が何でも運動量はヴェクタ(ベクタ)あってスケイラ(スカラー)ではないでしょう．

これを元に，時間微分をしたり，体積分を面積分に換えたりしながら，運動方程式を導くのだとおもいます．

ちなみに，私の手元にあるのは； 1) 流体力学，神部勉・著，裳華房，2003，ISBN:4-7853-2063-x 2) 連続体の力学，巽友正・著，岩波，2005, ISBN:4-00-007922-0 上記著者の「流体力学(新物理学シリーズ21)，培風館(1982)」も良いが入手困難． 3) 複素解析と流体力学，今井均・著，日本評論社，1996． 2次元流の複素関数論による説明は素晴らしいが，絶版のため高価．

もし善ければ，お使いの教科書をお教えくださいませんか？

Re: ベクトル解析　流体力学

いちさんのレス (2006/08/29(Tue) 14:45)

mNejiさんはじめまして，返信ありがとうございます

いま使っている参考書は「なっとくする流体力学」木田重雄，です

後期から流体力学の講義が始まるので予習の意味でいまから簡単そうな参考書を選んだのですが，公式の証明などで省略されている部分が多く，理解しづらいところがあります．（省略された部分を自分で考えるという意味ではいい勉強になるかもしれませんが）

mNejiさんがおっしゃっていた運動方程式を導く”流れ”はだいたい理解しているつもりなのですが，その過程での計算でつまづいてしまうんですよね．物理というよりは数学の問題なのかもしれません．

ネットで調べてみると参考書とは違うやり方がいろいろ見つかったので，そっちの方は理解できそうなのですが，なんとなくつまづいたところを放置するのも気持ち悪いんですよね．

Re: ベクトル解析　流体力学

toorisugari no Hiro さんのレス (2006/08/29(Tue) 17:03)

> この（uρu)というのがわかりません．間に・も×もなくただuとρuを並べただけの演算ってありましたでしょうか？

これはテンソルと呼ばれる表現です．

> ∫（−∇・（uρu))dV

これは単位時間あたり領域から出ていく運動量(輸送量)でベクトルとなります．

テンソルを含む量はどうしても添え字で考える必要があるようです．

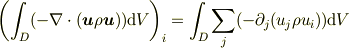
$\left(\int_{D}(-\nabla\cdot(\boldsymbol{u}\rho\boldsymbol{u}))\mathrm{d}V\right)_i &= \int_{D}\sum_{j}(-\partial_j(u_j\rho{u_i}))\mathrm{d}V$

とりあえず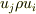， $u_j\rho{u_i}$ のように複数の添え字がつく量をテンソルと考えればいいでしょう．(この考え方は嫌いですが．．．)

上の量は「テンソルの微分」と言う複雑なものになっていますが，これ自身をイメージする必要はないと思います．微分で考えずに，これがもともと定義された状況においてイメージするのがよいと思います．

これを理解するには，ガウスの定理を拡張しなければいけません．

ガウスの定理にはいくつかのヴァリエーションがあります．

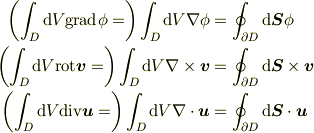
$\left(\int_{D}\mathrm{d}V\mathrm{grad}\phi = \right)\int_{D}\mathrm{d}V\nabla \phi &= \oint_{\partial D}\mathrm{d}\boldsymbol{S} \phi\\\left(\int_{D}\mathrm{d}V\mathrm{rot}\boldsymbol{v} = \right)\int_{D}\mathrm{d}V\nabla\times\boldsymbol{v} &= \oint_{\partial D}\mathrm{d}\boldsymbol{S}\times\boldsymbol{v}\\\left(\int_{D}\mathrm{d}V\mathrm{div}\boldsymbol{u} = \right)\int_{D}\mathrm{d}V\nabla\cdot\boldsymbol{u} &= \oint_{\partial D}\mathrm{d}\boldsymbol{S}\cdot\boldsymbol{u}$

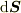( $\mathrm{d}\boldsymbol{S}$ 等を先頭に置くのが味噌です．上と同様にストークスの定理にもバリエーションがありますが省略します．第1,2式を通常のガウスの定理(第3式)から証明するには定ベクトルを内積でかけて整理すればよいです．)

これらはすべて

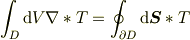
$\int_{D}\mathrm{d}V\nabla * T &= \oint_{\partial D}\mathrm{d}\boldsymbol{S} * T$

という形になっています．は任意のかけ算(スカラー倍，内積，外積)とします．この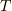はスカラーでもベクトルでも「それ以外の量」(つまりテンソル)でもかまわないとします．

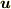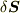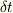さて，速度場 $\boldsymbol{u}$ で与えられた流体中のある面素 $\delta\boldsymbol{S}$ を微小時間 $\delta t$ の間に通過する流体の体積は 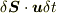$\delta\boldsymbol{S}\cdot\boldsymbol{u}\delta t$ ですから，この微小領域の運動量は

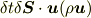
$\delta t \delta\boldsymbol{S}\cdot\boldsymbol{u}(\rho\boldsymbol{u})$

となります．よって，ある領域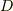を単位時間に出ていく流体の全運動量は

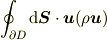
$\oint_{\partial D}\mathrm{d}\boldsymbol{S}\cdot\boldsymbol{u}(\rho\boldsymbol{u})$

になりますね．

これに「ガウスの定理」を適用すれば

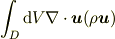
$\int_{D}\mathrm{d}V\nabla\cdot\boldsymbol{u}(\rho\boldsymbol{u})$

(微分は最後まで作用する．) ご質問の式になります．

先のテンソル量 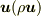$\boldsymbol{u}(\rho\boldsymbol{u})$ は微分を伴った形や単独で考えるより，面素をかけた形 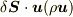$\delta\boldsymbol{S}\cdot\boldsymbol{u}(\rho\boldsymbol{u})$ 「面素を単位時間に通過した領域の運動量」(ベクトル量)で理解すればいいのです．

Re: ベクトル解析　流体力学

いちさんのレス (2006/08/29(Tue) 19:31)

toorisugari no Hiroさん詳しい説明ありがとうございます

なんとなく解決に近づいている気はするのですがテンソルという予想外の登場人物に戸惑っております．テンソルと行列は同じものですよね？

とりあえず頭を整理してテンソルの基本から勉強してみることにします

Re: ベクトル解析　流体力学

toorisugari no Hiro さんのレス (2006/08/29(Tue) 19:54)

> テンソルという予想外の登場人物に戸惑っております．

まあ，あまり深刻にならずそういう考え方もあるんだ程度でとどめて置いていいと思います．

> テンソルと行列は同じものですよね？

むう．どう説明しましょう．似たものであることには違いないのですが．．．

まず，行列は線形演算子を成分表示したもので，本質は演算子です．テンソルが行列と違うのはそれが物理量であるということです． (ですから，座標変換を表す行列はテンソルではありません．)

ふたつの物理量が比で結びつけられているとき (ex. 質量と体積 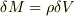$\delta M = \rho \delta V$ ) この比例定数を物理量と考えることがありますね． (上の例なら質量密度 $\rho$ です．)

上の例はスカラーとスカラーとの間の線形関係ですが，ベクトルとベクトルとの間の線形関係を考え，その「比例定数」を物理量と考える場合もあるはずです．これは行列で表されますが，これが物理量と見なされる場合テンソル(正確には2階のテンソル)と呼びます．(ま，つっこみどころ満載ですが．．．)

先の例だと面素(ベクトル)とそれを単位時間に通過する運動量(ベクトル)の間に比例関係があり，ふたつを結ぶ量として 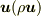$\boldsymbol{u}(\rho\boldsymbol{u})$ という運動量流束密度(テンソル)が定義されたと考えればいいでしょう．

これは，面素(ベクトル)とそれを単位時間に通過する電荷(スカラー)の間に比例関係があり，ふたつを結ぶ量として 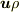$\boldsymbol{u}\rho$ という電流密度(ベクトル)が定義される話とパラレルです(ここでは $\rho$ は電荷密度と解釈します)．

あるいはもっと頻出する例として，流体中の領域の境界の一部をなす面素 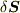$\delta \boldsymbol{S}$ を介して領域に作用する接触力 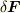$\delta \boldsymbol{F}$ が以下の関係を満たす

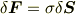
$\delta \boldsymbol{F}= \sigma \delta \boldsymbol{S}$

場合も考えられますね(パスカルの原理はご存じですね)． $\sigma$ がスカラーと見なせる場合，これを圧力(の負符号)というのはご存じでしょう．そうでない場合，粘性と関わるテンソルになります．(詳しい話はパス．)

テンソルと行列の違いにはそれが物理量か否か以外にも，重要な概念があるのですが，それは双対空間を勉強してからでいいと思います．それまでは「本当は違うんだけど，ほぼ同じ．」とこっそり思っておいてください．

Re: ベクトル解析　流体力学

mNeji さんのレス (2006/08/30(Wed) 11:46)

いちさん：

私も，流体力学の応用がしたくて入門書的な本を幾つか拝見しましたが，「？」の山が出来るだけでした...．これらの本は，どんな単語が，どんな場面で使われているを説明するだけで，その単語の意味を噛み砕いて説明するのではないと思います．

また，toorisugari no Hiroさんのご説明は，一般性の高い説明をされているので，とても難しくなっていて，私もまだ理解できません．

将来どんな分野での流体力学をされるのか判りませんが，上のご説明で判るように，流体力学は，数学とも密接な関係が高く，実用的には，航空機・船舶の設計指針を与えると共に，非等方性の高い連続流体や宇宙での電磁流体なども流体力学の範疇といえそうです．

でも，最初の勉強は，3次元ヴェクタ形式で，イメージをしっかりしながら勉強するので良いのだと思います．

Re: ベクトル解析　流体力学

いちさんのレス (2006/08/30(Wed) 14:07)

toorisugari no Hiroさん，mNejiさん，親切な回答本当にありがとうございました，感謝しています．

どんなことでも，完全に理解するというのは難しいことだと思うのですが，おかげで随分理解は深まりました．

ある程度のところで自分を納得させて先に進むというのも必要なのかもしれませんね（疑問を忘れるのではなく）

Re: ベクトル解析　流体力学

toorisugari no Hiro さんのレス (2006/08/31(Thu) 15:56)

mNejiさん:

> また，toorisugari no Hiroさんのご説明は，一般性の高い説明をされているのでとても難しくなっていて，私もまだ理解できません

うう，すいません．なかなか上手に説明できないですね．というより，まだ理解できていないのでしょう．

> これらの本は，どんな単語が，どんな場面で使われているを説明するだけで，その単語の意味を噛み砕いて説明するのではないと思います．

電磁気学や流体力学って空間の理解や運動学(記述法)だけで半分以上紙面を費やしています．それでも，まだ，イメージにつながる表現は難しいので「噛み砕」けないのでしょう．

テンソルも古い物理流の定義(座標変換規則に従う添え字つきの量)や数学流の定義((双対)ベクトル空間に対する多重線形写像)などありますが，ともに計算や理論展開はできても「物理的イメージ」につながらない．結構つらいものがあります．

(そもそも双対ベクトル空間って物理的に何よ．という疑問があります．保存力の空間がそうかもしれませんが，一般の力も双対ベクトル空間に属するのか?と考え出すと．．．)

[home] [掲示板] [ページの先頭]

ベクトル解析 流体力学

ベクトル解析　流体力学