クーロンの法則
クーロンの法則
Chippy さんの書込 (2006/08/26(Sat) 12:18)
初めまして.英文の問題なのですが(アメリカの物理の問題です).全然解けずに困っています. どなたか解き方を教えてください.
Three charges Q1,Q2,and Q3 are located in a straight line. Q1= (1.90×10^-6) C and Q2= (-3.22×10^-6) C are fixed at their positions, distance 0.235 m apart, and the charge Q3= 3.18×10^-6) C is moved along the straight line. For what position of Q3 relative to Q1 is the net force on Q3 due to Q1 and Q2 zero? Use the plus sign for Q3 to the right of Q1.
Re: クーロンの法則
mNeji さんのレス (2006/08/26(Sat) 13:09)
始めまして.
問題を日本語にしてみてください.その次に,何処までなら解く事ができるか示してください.日本語にするときに,疑問の部分があるかどうか気をつけてね.
【ヒント】相対値で計算できますね.
Re: クーロンの法則
ガージ さんのレス (2006/08/27(Sun) 02:40)
mNejiさん回答ありがとうございます.
Q1= (1.90×10^-6) C の右隣0.235mに Q2= (-3.22×10^-6) C があり. また Q2の右隣(x)mに Q3= (3.18×10^-6) C があり.Q1,2は固定され,Q3は自由に左右に動ける.Q3のForceの合計=0の時,Q3はQ1からどれだけ離れているか? (右向き方向を正とする)
Force of between Q1 & Q2 ={k×(1.90×10^-6)(3.18×10^-6)}/(0.235+x)^2
Force of between Q1 & Q3 ={-k×(1.90×10^-6)(3.22×10^-6)}/(x)^2
(Force of between Q1 & Q3 )+(Force of between Q1 & Q2) =0
0= { {-k×(1.90×10^-6)(3.22×10^-6)}/(x)^2 }+ { {k×(1.90×10^-6)(3.18×10^-6)}/(0.235+x)^2}
{k×(1.90×10^-6)(3.22×10^-6)}/(x)^2= {k×(1.90×10^-6)(3.18×10^-6)}/(0.235+x)^2
このような感じで考え解きましたが,自信が全くありません・・・.
Re: クーロンの法則
mNeji さんのレス (2006/08/27(Sun) 09:01)
>Three charges Q1,Q2,and Q3 are located in a straight line. >Q1= (1.90×10^-6) C and Q2= (-3.22×10^-6) C are fixed at their positions, >distance 0.235 m apart, and the charge Q3= 3.18×10^-6) C is moved along the >straight line. For what position of Q3 relative to Q1 is the net force on Q3 >due to Q1 and Q2 zero? Use the plus sign for Q3 to the right of Q1.
上の問題を直訳してみます.
3つの電荷Q1,Q2,そしてQ3がある直線上に配置されていた. Q1=1.9μCで Q2=-3.22μCであり其々の位置は距離0.235m離れて固定されていて,そしてQ3=3.18μCでその直線に従って移動される(事ができる).Q1に対するQ3の位置がどれだけならば,Q1およびQ2がQ3へ働く正味の力がゼロになるか? Q3(の位置)をQ1の右方向に正とするように(座標を)用いよ.
図を考えると <pre>
+1.90μC+3.18μC -3.22μC
Q1Q3Q2 ・−−・−−−−−−−・ 0 x(m) 0.235m
x負 ← ・ → x正 </pre>
Q3が正の電荷をもち,クーロン力の符号つきの相対値だけが必要だから,以下に示すような略記とする.
Q1がQ3に及ぼす力:F1=k*1.90*x^(-2) Q2がQ3に及ぼす力:F2=k*(-3.22)*(0.235-x)^(-2)
題意より:F1+F2=0 よって k*1.90*x^(-2)+k*(-3.22)*(0.235-x)^(-2)=0
整理して (0.235-x)^2=(3.22/1.90)x^2
辺々の平方根をとると 0.235-x=+/-sqrt(322/190)x=+/-1.302x
整理して (+/-1.302+1)x=0.235 x=0.235/(2.302 or -0.302)=+0.102 or -0.779
したがって,Q3に働く正味の力が消失するのは; 1) Q1からQ2にむかって0.102m 2) Q1からQ2の逆にむかって0.779m の2地点である.
と思われます.
なお,今後のために,出典を無理の無い範囲でお教えくださると幸いです.
Re: クーロンの法則
mNeji さんのレス (2006/08/27(Sun) 09:36)
訂正:
xが負の領域は良いのですが,xが正の場合,
a) 0<x<0.235m :解なし F1=正 (斥力) F2=正 (引力) いくら加算してもゼロになれない.
b) 0.235m <= x :解なし F1=正 (斥力) F2=負 (引力) |F1| << |F2| 符号は逆でも,絶対値が違うので,加算してゼロにならない.
結局,x>0には解なし.
取りあえず,上記のように訂正します.御免なさい.
Re: クーロンの法則
ガージとChippy さんのレス (2006/08/29(Tue) 08:16)
mNejiさんお返事遅れてすいません 詳しい解説本とうにありがとうございます.
今後の学習の為にいくつか質問があります. >Q1がQ3に及ぼす力:F1=k*1.90*x^(-2) >Q2がQ3に及ぼす力:F2=k*(-3.22)*(0.235-x)^(-2) (−3.22)はプラスではいけないのでしょうか?
もし負の数の距離を答えとして良い場合は-0.779mが答えとなるのでしょうか?
よく間違えるのが距離の解が2つ出る時にその際どちらが正解の値かいまいち良く判りません(今回の場合のように).どのように見極めれば良いのでしょうか?
Re: クーロンの法則
mNeji さんのレス (2006/08/29(Tue) 09:29)
>よく間違えるのが距離の解が2つ出る時にその際どちらが正解の値かいまいち良く判りません(今回の場合のように).どのように見極めれば良いのでしょうか?
1次元配置の計算では,ベクトルを使うと大げさな気がして,逆に良く間違えるようです.検討しますので,しばらくお持ちください.
Re: クーロンの法則
mNeji さんのレス (2006/08/30(Wed) 11:17)
>問題の答えは-0.779mでよろしいですか?
以前に書きました,No.11519 の2)の回答; >2) Q1からQ2の逆にむかって0.779m
は,そこに示した図の意味でよければ,「-0.779m」で良いとおもいます.
しかし,この問題をよく読むと,Q3座標のとり方は「Q1の右に正」とれと書いてありますが,Q2に付いての記述がありません.そこであえて符号に拠らない回答をいたしました.
そこで,正式な米国機関ないしは大学の試験問題としては変則的な気がしましたので,米国留学を目指しているであろう若人のために出典をお聞きした次第です.
Re: クーロンの法則
Chippy さんのレス (2006/08/30(Wed) 20:32)
mNejiさんありがとうございます.
ちょっと文章的にも判りにくい問題でした.この出典は学校でもらったプリント問題です.
よく間違えるのが距離の解が2つ出る時にその際どちらが正解の値かいまいち良く判りません(今回の場合のように).どのように見極めれば良いのでしょうか?
例えば,3つの正電荷がx軸上に並んでいるとします.
(x_1)=2.86μC 原点(x_3)=0.3μC (x_2)=8.4μC ---------(-4.2m) ---・---(Y m)----------(X m)------*-----
原点から8.4μCまでの距離を10.8mとするときの0.3μC の距離Ymを求めたいとします. F(x_1)=(K)(2.86μ)/(15-x)^2 F(x_2)=(K)(8.4μ)/(x)^2
F(x_1)=F(x_2) (2.86μ)/(15-x)^2 = (8.4μ)/(x)^2 2.86(x^2) = 8.4(15-x)^2 5.54(x^2)-252(x)+1890 = 0
そうすると x=9.468 , 36.022
Y=10.8-9.68 , Y=10.8-36.022のいずれかが解になると思います.しかし,先の問題のように一方が誤っているとどの様にわかるのですか?
Re: クーロンの法則
mNeji さんのレス (2006/08/31(Thu) 00:00)
回答が遅れています.現在,この数式掲示版で使えるLaTeXのテンプレート制作に頭が没頭状態の為に,細かな解説に思考が追いつきません.
その上,また違う問題を出されていらっしゃいますが,今度の問題は,以前の問題以上に解読が不可能に近いと思います.質問する上で,もう少し表現に注意を払っていただかないと,答えられないと思います.
さて,ご質問の件ですが,ある意味では簡単なことです.2点の電荷同士の電気力は,x軸上にあっても,2点の位置が左右交代すると符号が変わってしまうからです.
この手の問題は,私はこの掲示版に来てから3回目ですが,上の注意を払えば簡単になります.No.11519の場合でいえば,その図をコピーし,力の方向も書き入れますと;
<pre> F1の符号:-F1の符号:+ F1の符号:+ F2の符号:+F2の符号:+ F2の符号:-
××
Q1との力F1:斥力Q2との力F2:引力
+1.90μC+3.18μC -3.22μC
Q1Q3Q2 ・−−・−−−−−−−・ 0 x(m) 0.235m
x負 ← ・ → x正
</pre>
こうすると,力がバランスするには,当たり前ですが
条件1) F1とF2の方向が逆であること. 条件2) その大きさが等しいこと
が必要です.
中央部分は,条件1)にあわないので,除外されます. Q2より右の部分は,条件1)に合うものの,電荷の小さいQ1が,電荷の大きいQ2より遠いので,条件2)に合えません.
従って,許されるのは,Q1より左の部分だけです.
Re: クーロンの法則
mNeji さんのレス (2006/08/31(Thu) 23:31)
詰まらない会合のさなかに,ノートを書けたので,速報します.
線分の上に固定電荷Q,試験電荷qがあるとします.線分上のある点Oから試験電荷qの位置を(x)とし,固定電荷の位置を(X)とします.そして固定電荷からqを見る相対座標を(r)とします.画にすると; <pre> 《図1 座標の表し方 》
r≡x−X ・−−−−−−−−−→・ 0Xx −−−−−・−−−−−−−−−・−−−−−−−−−−・−−−→ + 原点O固定電荷Q試験電荷q </pre>
こう決めておけば,固定電荷Qより試験電荷qが ・右ならrは正, ・左ならrは負, となります.当たり前です.
固定電荷Qが試験電荷qの場所に作るポテンシャルPは,
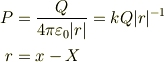
 は,極座標の動径半径と違って,正負を取る為に絶対値をつけています.
は,極座標の動径半径と違って,正負を取る為に絶対値をつけています.
すると,固定電荷Qが試験電荷qの場所に作るx軸方向の電場Eは,
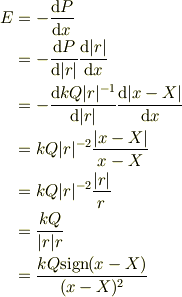
ここで
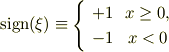
最終的に,Qが作り出す電場がqに与える力Fは,+xの方向に正とすると;
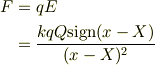
Re: クーロンの法則
Chippy さんのレス (2006/09/02(Sat) 07:46)
mNejiさん
お忙しい中,とてもわかりやすい解説をして頂きまして本当にありがとうございます.
図解説,公式展開等とても学習の参考になりました.
本当にありがとうございました.