滑車が質量を持っている場合
滑車が質量を持っている場合
ミストレスS さんの書込 (2006/08/23(Wed) 12:39)
院試を後日に控えている者です.物理の専攻ではないのですが, 試験科目に物理がありまして,現在悪戦苦闘しております. 過去問によく分からない問題があったので質問させて下さい.
?直径D,質量Mの滑車を天井に取り付ける. ?質量が無視できる紐の両端にそれぞれ質量M1,M2のおもりを結んで, 滑車に紐を引っ掛ける.
滑車と紐の摩擦は大きく,紐は滑車の車輪を滑らないとして, この時のおもりの加速度を求めよ.ただし重力加速度をgとする.
というものです. 滑車の質量が無視出来る場合はすぐ出来るのですが,無視出来ない場合, そのモーメントをどのように処理すれば良いのかがよく分かりません. 高校物理程度での解説をして頂けたらと思います. あ,でも微積程度ならOKです.
よろしくお願いします.
Re: 滑車が質量を持っている場合
mNeji さんのレス (2006/08/23(Wed) 13:00)
始めまして.
これから出かけるので,簡単に説明します.
滑車の中心に座標があるとします.滑車中心は固定されているので原点の周りの角運動量の時間微分が外部トルクにより起こる式を書きます.初期条件は題意に従い追加する.
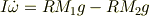
ここで
滑車半径:  滑車角速度:
滑車角速度:  滑車慣性能率:
滑車慣性能率: 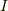
慣性能率は滑車の構造によって異なります.問題をよく読んで下さい.何も書いてなければ,この問題は不完全ですから,実試験の時は,後に残して余裕があれば監督官に異議申し立てをした上で,均一な円板を仮定して解けばよいでしょう.ちなみに
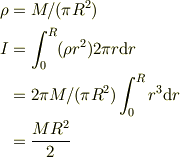
Re: 滑車が質量を持っている場合
ミストレスS さんのレス (2006/08/23(Wed) 19:07)
早速のご回答をありがとうございます. v=Rωだからa=R(ω)'で,このaが解答という感じと受け取りました. ちなみに滑車の形は,図を見る限りでは円形だと思います. するとI=(1/2)MR^2なので,a=2R^2((M1-M2)/M)g ということで,問題ないでしょうか.
Re: 滑車が質量を持っている場合
山旅人 さんのレス (2006/08/23(Wed) 19:41)
こんにちは.山旅人と申します.横から失礼いたします.
失礼ながら,mNeji さんが挙げられた式は,やや追求不足のようです.
M 1 >M 2 として,M 1 を吊る紐の張力を T 1 ,M 2 を吊る紐の張力を T 2 ,おもりの上下運動の加速度の大きさを α,滑車の回転の角加速度の大きさを β とすると,
M 1 の運動方程式M 1 g−T 1 =M 1 α… (1) M 2 の運動方程式T 2 −M 2 g=M 2 α… (2) 滑車の運動方程式Iβ=R(T 1 −T 2 )… (3) 紐が滑らないからα=Rβ… (4)
(1)〜(4)から β を求めると,β=R(M 1 −M 2 )g/{I+R 2 (M 1 +M 2 )}=2(M 1 −M 2 )g/{M+2(M 1 +M 2 )}R
よって,α=Rβ=<b>2(M 1 −M 2 )g/{M+2(M 1 +M 2 )}</b>
Re: 滑車が質量を持っている場合
mNeji さんのレス (2006/08/23(Wed) 21:22)
済みませんでした.山旅人さんの結論が正しいとおもいます.
そこで,少し奇妙な別解を示します.
左右の重りが見掛け上,つねに糸の根元にいると考えます.すると慣性能率の計算で,それぞれの重りが,原点からRの位置で回転するのとおなじですから,真の慣性能率 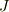 とすると
とすると
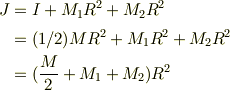
この慣性能率を用いて角運動量の方程式は
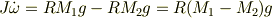
そこで物体の加速度は
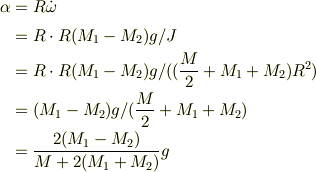
訂正すると共に,お詫びします.
ベストを尽くされるように.(回答作成後,次元解析は常にしましょう)
追伸:
典型的な慣性能率(モーメント)は,Johさんによるレポート記事があります.
●色々な物体の慣性モーメント1 [物理のかぎしっぽ]
Re: 滑車が質量を持っている場合
ミストレスS さんのレス (2006/08/24(Thu) 00:08)
おかげさまでモーメントの運動方程式の記述の仕方が分かりました. もう少し他の問題で演習して馴染ませていきたいと思います. mNejiさん,山旅人さん,どうもありがとうございました.
追記 あ,次元解析には気をつけます・・・ご指南どうもです.